北师版数学七年级上册《第四章 基本平面图形》单元检测B卷
试卷更新日期：2021-08-15 类型：单元试卷
一、单选题
-
1. 如图中的直线表示方法中，正确的是________（填序号）.
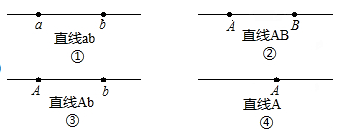A、① B、② C、③ D、④2. 如果A，B，C三点在线段AB上，且线段AB＝10cm，BC＝4cm，若M，N分别为AB，BC的中点，那么M，N两点之间的距离为（ ）A、3cm B、7cm C、5cm或1cm D、7cm或3cm3. 下列四个图中，能用 、 、 三种方法表示同一个角的是（ ）A、
B、
C、
D、
4. 过多边形的一个顶点能引出7条对角线，则这个多边形是（ ）边形A、七 B、八 C、九 D、十5. 如图，将一根绳子对折以后用线段AB表示，现从P处将绳子剪断，剪断后的各段绳子中最长的一段为60cm，若AP＝ PB，则这条绳子的原长为（ ）
A、100cm B、150cm C、100cm或150cm D、120cm或150cm6. 如图，点A，B，C顺次在直线上，点M是线段AC的中点，点N是线段BC的中点，已知AB=16cm，MN=（ ）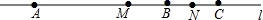
A、6cm B、8cm C、9cm D、10cm7. 下列说法中正确的是( )A、8时45分，时针与分针的夹角是30° B、6时30分，时针与分针重合 C、3时30分，时针与分针的夹角是90° D、3时整，时针与分针的夹角是90°8. 如图，直线AB ， CD相交于点O ， OF⊥OC于O ， OE平分∠AOF ， 如果∠COE=15°，那么∠BOD的度数是（ ）
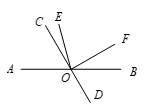A、75° B、50° C、60° D、70°9. 如图， 是 的平分线， ， ，则 的度数为（ ）
A、 B、 C、 D、10. 借助一副三角尺不能画出的角是（ ）A、 B、 C、 D、11. 如图，∠AOC＝90°，OC平分∠DOB，且∠DOC＝22°36′，∠BOA度数是（ ）
A、67°64′ B、57°64′ C、67°24′ D、68°24′12. 如图，在线段AB上有C，D两点，CD长度为1cm，AB长为整数，则以A，B，C，D为端点的所有线段长度和不可能为（ ）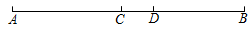
A、16cm B、21cm C、22cm D、31cm二、填空题
-
13. 整理教室时，老师总是先把每一列最前和最后的课桌摆好，然后再依次摆中间的课桌，一会儿一列课桌便整整齐齐摆在了一条线上，这其中蕴含的数学道理是 ．14. 如下图，已知点C在线段 上，点M、N分别是 、 的中点，且 ，则 的长度为 .
15. 在一条直线上取A、B、C三点，使得AB = 9厘米，BC = 4厘米，如果O是线段AC的中点，则线段OA的长为 ．16. 把16.42° 用度分秒表示为 ；把71°4′30″用度表示为度.17. 如图，直线AB，CD相交于点O，EO⊥AB，垂足为点O，若∠AOD＝132°，则∠EOC＝°．
18. 如图， 平分 ，则 °.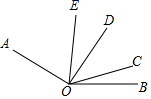
三、解答题
-
19. 如图，平面上有A、B、C、D四个点，根据下列语句画图.
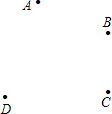
（ 1 ）画直线AB，作射线AD，画线段BC；
（ 2 ）连接DC，并将线段DC延长至E，使DE＝2DC.
20. 如图，点A，O，E在同一条直线上，∠AOB=40°，∠COD=28°，OD平分∠COE，求∠DOB的度数.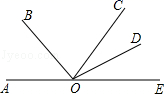
21. 如图，线段 上有点C和点D， ， ，且 的中点M和 的中点N之间的距离是40cm，求 的长．
22. 如图，已知∠AOB＝90°，∠COD＝90°，OE为∠BOD的平分线，∠BOE＝18°，求∠AOC的度数.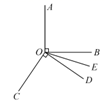
23. 如图， ， 是 的平分线， 是 的平分线，若 .
(1)、求 的度数；(2)、若没有给出 的度数，你能否求出 的度数？请说明理由；(3)、在（2）的条件下，若 ，求 的度数，你能从中发现什么规律？24. 综合与实践问题情境
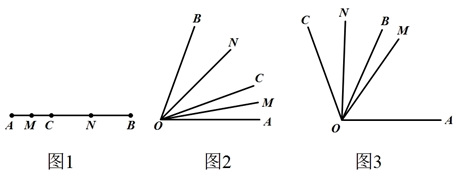
在数学活动课上，老师和同学们以“线段与角的共性”为主题开展数学活动，发现线段的中点的概念与角的平分线的概念类似，甚至它们在计算的方法上也有类似之处，它们之间的题目可以转换，解法可以互相借鉴．如图1，点C是线段AB上的一点，M是AC的中点，N是BC的中点．
(1)、问题探究①若AB=6，AC=2，求MN的长度．（写出计算过程）
②若AB=a ， AC=b ， 则MN= ▲ ． （直接写出结果）
(2)、继续探究“创新”小组的同学类比想到：如图2，已知∠AOB=70°，在角的内部作射线OC ， 再分别作∠AOC和∠BOC的角平分线OM ， ON ．
③若∠AOC=20°，求∠MON的度数．（写出计算过程）
④若∠AOC=m ， 则∠MON= ▲ ． （直接写出结果）
(3)、深入探究“慎密”小组在“创新”小组的基础上提出：如图3，若∠AOB=n ， 在角的外部作射线OC ， 再分别作∠AOC和∠BOC的角平分线OM ， ON ， 若∠AOC=m ， 则∠MON= ． （直接写出结果）