2021-2022学年数学八年级上册第十一章 三角形 单元测试卷

试卷更新日期：2021-08-15 类型：单元试卷

进入 出卷网 下载

一、单选题

  • 1. 如图所示，以线段BC为一边的三角形共有（ ）

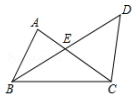    A、1个 B、2个 C、3个 D、4个

    查看试题解析

  • 2. 下列多边形中，对角线是5条的多边形是（   ）
    A、四边形 B、五边形 C、六边形 D、七边形

    查看试题解析

  • 3. 下列图形中具有稳定性的是（  ）
    A、 B、 C、 D、

    查看试题解析

  • 4. 如图，∠ABD、∠ACD的角平分线交于点P ， 若∠A＝60°，∠D＝20°，则∠P的度数为（   ）

    A、15° B、20° C、25° D、30°

    查看试题解析

  • 5. 正十二边形的外角和的度数为（   ）
    A、1800° B、720° C、360° D、180°

    查看试题解析

  • 6. 如图，BP是△ABC中∠ABC的平分线，CP是∠ACB的外角的平分线，如果∠ABP=20°，∠ACP=50°，则∠A=（ ）.

    A、60° B、80° C、70° D、50°

    查看试题解析

  • 7. △ABC中，∠ABC与∠ACB的平分线相交于I，且∠BIC=130°，则∠A的度数是（   ）
    A、40° B、50° C、65° D、80°

    查看试题解析

  • 8. 如图，已知△ABC中，AD，AE，AF分别是三角形的高线，角平分线及中线，那么下列结论错误的是（    ）

    A、AD⊥BC B、BF=CF C、BE=EC D、∠BAE=∠CAE

    查看试题解析

  • 9. 如图，在 △ABC中，AD，AE 分别是 △ABC的角平分线和高线，用等式表示∠DAE、∠B、∠C的关系正确的是（   ）

    A、2∠DAE=∠B−∠C B、2∠DAE=∠B+∠C C、∠DAE=∠B−∠C D、3∠DAE=∠B+∠C

    查看试题解析

  • 10. 如图，在△ABC中，AD是BC边上的中线，点E是AD的中点，过点E作EF⊥BC于点F.已知BC＝10，△ABD的面积为12，则EF的长为（ ）

    A、1.2 B、2.4 C、3.6 D、4.8

    查看试题解析

二、填空题

  • 11. 已知，三角形的三边长为3，5，m，则m的取值范围是 ．

    查看试题解析

  • 12. 等腰三角形一腰上的高与另一腰所成的夹角为45°，则这个等腰三角形的顶角的度数为.

    查看试题解析

  • 13. 如果一个正方形被截掉一个角后，得到一个多边形，那么这个多边形的内角和是 ．

    查看试题解析

  • 14. 如图，在△ABC中，∠ACB=60°，∠BAC=75°，AD⊥BC于D，BE⊥AC于E，AD与BE交于H，则∠CHD=

    查看试题解析

  • 15. 如图，在△ABC 中，已知点 D、E、F 分别是边 BC、AD、CE 上的中点，且 S△ABC=4， 则 S△BEF= ．

    查看试题解析

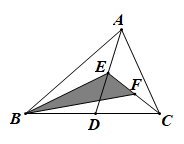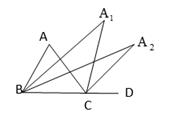  • 16. 如图，∠ACD是△ABC的一个外角，∠ABC的平分线与∠ACD的平分线交于点 A1 ， ∠A1BC  的角平分线与 ∠A1CD 的平分线交于点 A2 ，若∠A＝60°，则 ∠A2 的度数为

      

    查看试题解析

  • 17. 如图，蚂蚁点 M 出发，沿直线行走4米后左转36°，再沿直线行走4米，又左转36°，照此走下去，他第一次回到出发点 M ，一共行走的路程是 .

    查看试题解析

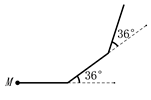  • 18. 如图，△ABC中，∠A=40°，∠B=70°，CE平分∠ACB，CD⊥AB于D，DF⊥CE，则∠CDF =度．

    查看试题解析

三、解答题

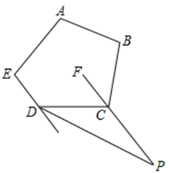
  • 19. 已知a，b，c是三角形的三边长．
    (1)、化简：|a-b-c|+|b-c-a|+|c-a-b|；
    (2)、在（1）的条件下，若a=5，b=4，c=3，求这个式子的值．

    查看试题解析

  • 20. 如图，在五边形ABCDE中，∠A+∠B+∠E=310°，CF平分∠DCB，FC的延长线与五边形ABCDE外角平分线相交于点P，求∠P的度数

    查看试题解析

  • 21. 三角形的内角和为180°，已知三角形的第一个内角是第二个内角的3 倍，第三个内角比第二个内角小20°，求三角形每个内角的度数？

    查看试题解析

  • 22.

    如图，在△ABC中，AB=AC，D、E分别在AC、AB边上，且BC=BD，AD=DE=EB，求∠A的度数．


    查看试题解析

  • 23.

    将一副三角板中的两块直角三角尺的直角顶点C按如图方式叠放在一起（其中，∠A=60°，∠D=30°；∠E=∠B=45°）：

    （1）①若∠DCE=35°，求∠ACB的度数；

    ②若∠ACB=150°，求∠DCE的度数；

    （2）由（1）猜想∠ACB与∠DCE的数量关系，并说明理由．

    （3）请你动手操作，现将三角尺ACD固定，三角尺BCE的CE边与CA边重合，绕点C顺时针方向旋转，当0°＜∠ACE＜180°且点E在直线AC的上方时，这两块三角尺是否存在一组边互相平行？若存在，请直接写出∠ACE角度所有可能的值（不必说明理由）；若不存在，请说明理由．


    查看试题解析

  • 24. 回答下列问题：
    (1)、如图①， △ABC 的内角 ∠ABC 的平分线与外角 ∠ACD 的平分线相交于P点， ∠A=40° ， ∠P 的度数=（直接写出答案）．

    (2)、如图②，四边形ABCD中，设 ∠A=α ， ∠D=β ， ∠P 为四边形ABCD的内角 ∠ABC 与外角 ∠DCB 的平分线所在直线相交而形成的锐角，如图②，若 α+β>180° ，求 ∠P 的度数（用 α ， β 的代数式表示，写出详细过程）．

    查看试题解析

  • 25. 如果一个多边形的各边都相等，且各内角也都相等，那么这个多边形就叫做正多边形．如图，就是一组正多边形，观察每个正多边形中∠α的变化情况：

    (1)、将下面的表格补充完整：
    (2)、根据规律，是否存在一个正多边形，其中的∠α=21°？若存在，请求出n的值，若不存在，请说明理由．

    正多边形边数

    3

    4

    5

    6

    …

    n

    ∠α的度数

    60°

    …

    查看试题解析

  • 26. 已知：如图1，线段AB、CD相交于点O，连接AD、CB，如图2，在图1的条件下，∠DAB和∠BCD的平分线AP和CP相交于点P，并且与CD、AB分别相交于M、N，试解答下列问题：

    (1)、在图1中，请直接写出∠A、∠B、∠C、∠D之间的数量关系：；
    (2)、在图2中，若∠D=40°，∠B=30°，试求∠P的度数(写出解答过程)；
    (3)、如果图2中，∠D和∠B为任意角，其他条件不变，试写出∠P与∠D、∠B之间的数量关系(直接写出结论即可).

    查看试题解析