北师版数学七年级上册《第四章 基本平面图形》单元检测A卷
试卷更新日期:2021-08-15 类型:单元试卷
一、单选题
-
1. 过平面上
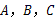 三点中的任意两点作直线,可作( ) A、1条 B、3条 C、1条或3条 D、无数条2. 如图,已知三点A,B,C画直线AB,画射线AC,连接BC,按照上述语句画图正确的是( )A、
三点中的任意两点作直线,可作( ) A、1条 B、3条 C、1条或3条 D、无数条2. 如图,已知三点A,B,C画直线AB,画射线AC,连接BC,按照上述语句画图正确的是( )A、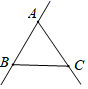 B、
B、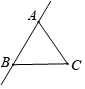 C、
C、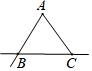 D、
D、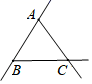 3. 下图中标注的角可以用∠O来表示的是( )A、
3. 下图中标注的角可以用∠O来表示的是( )A、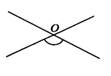 B、
B、 C、
C、 D、
D、 4. 如图,OC平分∠AOD,OD平分∠BOC,下列等式不成立的是( )
4. 如图,OC平分∠AOD,OD平分∠BOC,下列等式不成立的是( )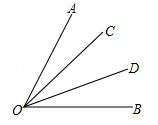 A、∠AOC=∠BOD B、∠COD= ∠AOB C、∠AOC= ∠AOD D、∠BOD= ∠BOC5. 从十二边形的一个顶点出发,可引出对角线( )条A、9条 B、10条 C、11条 D、12条6. 如图,在不添加字母的情况下,可以用字母表示出来的不同线段和射线有( )
A、∠AOC=∠BOD B、∠COD= ∠AOB C、∠AOC= ∠AOD D、∠BOD= ∠BOC5. 从十二边形的一个顶点出发,可引出对角线( )条A、9条 B、10条 C、11条 D、12条6. 如图,在不添加字母的情况下,可以用字母表示出来的不同线段和射线有( ) A、3条线段,3条射线 B、6条线段,6条射线 C、6条线段,4条射线 D、3条线段,1条射线7. 下列说法中,错误的是( ).A、两点之间,线段最短 B、若线段 ,则点 是线段 的中点 C、两点确定一条直线 D、直线 和直线 是同一条直线8. 如果A,B,C三点同在一直线上,且线段AB=6cm,BC=3cm,A,C两点的距离为d,那么d=( )A、9cm B、3cm C、9cm或3cm D、大小不定9. 如图, 是 的中点, 是 的中点,则下列等式中正确的是( )
A、3条线段,3条射线 B、6条线段,6条射线 C、6条线段,4条射线 D、3条线段,1条射线7. 下列说法中,错误的是( ).A、两点之间,线段最短 B、若线段 ,则点 是线段 的中点 C、两点确定一条直线 D、直线 和直线 是同一条直线8. 如果A,B,C三点同在一直线上,且线段AB=6cm,BC=3cm,A,C两点的距离为d,那么d=( )A、9cm B、3cm C、9cm或3cm D、大小不定9. 如图, 是 的中点, 是 的中点,则下列等式中正确的是( )① ;② ;③ ;④ .
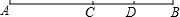 A、①② B、③④ C、①④ D、②③10. 周末早上,小兰9:00从家里出发去图书馆看书,上午10:30回到家中,这段时间内钟面上的时针转了( )
A、①② B、③④ C、①④ D、②③10. 周末早上,小兰9:00从家里出发去图书馆看书,上午10:30回到家中,这段时间内钟面上的时针转了( ) A、37.5° B、45° C、52.5° D、60°11. 如图,已知 , , 平分 , 平分 ,则 的度数为( )
A、37.5° B、45° C、52.5° D、60°11. 如图,已知 , , 平分 , 平分 ,则 的度数为( )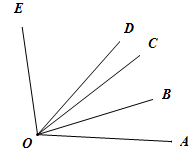 A、 B、 C、 D、12. 如图,将一副三角板叠在一起使直角顶点重合于点O , (两块三角板可以在同一平面内自由转动,且 , 均小于180°),下列结论一定成立的是( )
A、 B、 C、 D、12. 如图,将一副三角板叠在一起使直角顶点重合于点O , (两块三角板可以在同一平面内自由转动,且 , 均小于180°),下列结论一定成立的是( )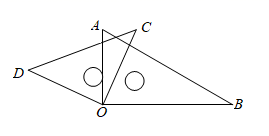 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
13. 要把一根木条在墙上钉牢,至少需要2枚钉子.其中蕴含的数学道理是.14. 已知 三点在同一条直线上,线段 ,则 .15. 如图, 是 的中点, 分别在 上,且 ,则 .
 16. °.17. 如图AO⊥BO, , 平分 ,则 的度数为 .
16. °.17. 如图AO⊥BO, , 平分 ,则 的度数为 . 18. 如图,直线EF,CD相交于点O,OA⊥OB,OD平分∠AOF,若∠FOD=4∠COB,则∠AOE .
18. 如图,直线EF,CD相交于点O,OA⊥OB,OD平分∠AOF,若∠FOD=4∠COB,则∠AOE .
三、解答题
-
19. 如图所示,AO⊥FD,OD为∠BOC的平分线,OE为射线OB的反向延长线,若∠AOB=40°,求∠EOF、∠COE的度数.
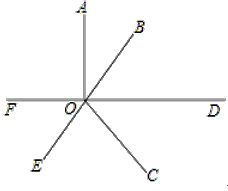 20. 如图,在△ABC中,∠A=40°,∠B=76°,CE平分∠ACB,CD⊥AB于点D,DF⊥CE于点F,求∠CDF的度数.
20. 如图,在△ABC中,∠A=40°,∠B=76°,CE平分∠ACB,CD⊥AB于点D,DF⊥CE于点F,求∠CDF的度数. 21. 已知:如图,点B和点D在线段AC上,若BD= AB= CD,E为线段AB的中点,BC=6cm,求线段ED的长度.
21. 已知:如图,点B和点D在线段AC上,若BD= AB= CD,E为线段AB的中点,BC=6cm,求线段ED的长度. 22. 如图,已知C,D两点将线段AB分成三部分,且这三部分的长度之比为2:3:4,点M为线段AB的中点,BD=8cm,求线段DM的长.
22. 如图,已知C,D两点将线段AB分成三部分,且这三部分的长度之比为2:3:4,点M为线段AB的中点,BD=8cm,求线段DM的长. 23. 如图, 为直线 上的一点, 为直角, 平分 .若 平分 ,且 ,求 的度数.
23. 如图, 为直线 上的一点, 为直角, 平分 .若 平分 ,且 ,求 的度数.