北师版数学七年级上册《第三章整式及其加减》单元检测B卷

试卷更新日期：2021-08-15 类型：单元试卷

进入出卷网下载

一、单选题

1. 下列式子书写正确的有（）
（1）2×b （2）m÷3 （3） $2 \frac{1}{2} a b$ （4）90﹣c （5）m+n万元

A、1个 B、2个 C、3个 D、4个

查看试题解析
2. 将 $2 (x + y) + 3 (x + y) - 4 (x + y)$ 合并同类项，得（）

A、x+y B、-x+y C、-x-y D、x-y

查看试题解析
3. 如果 $2 x^{2} y^{b + 1}$ 与 $- 4 x^{a} y^{3}$ 是同类项，则 $a ， b$ 的值分别是（）

A、 $1 ， 2$ B、 $2 ， 1$ C、 $2 ， 2$ D、 $2 ， 3$

查看试题解析
4. 下列各式中与多项式 $a - b - c$ 不相等的是（）

A、 $a - (b + c)$ B、 $a - (b - c)$ C、 $(a - b) + (- c)$ D、 $- b - (c - a)$

查看试题解析
5. 今年金鸡百花奖有 $a$ 部作品参赛，比上届参赛作品增加了 $40 %$ 还多2部，上届参赛作品有（）

A、 $\frac{a + 2}{1 + 40 %}$ B、 $(1 + 40 %) a + 2$ C、 $\frac{a - 2}{1 + 40 %}$ D、 $(1 + 40 %) a - 2$

查看试题解析
6. 若x²﹣3x＝4，则3x²﹣9x+8的值是（）

A、20 B、16 C、4 D、﹣4

查看试题解析
7. 按如图所示的程序计算，若开始输入的数为 $x = 5$ ，则最后输出的结果是（）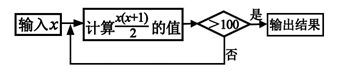

A、15 B、30 C、105 D、120

查看试题解析
8. 下列结论中，正确的是（）

A、单项式 $\frac{3 x y^{2}}{7}$ 的系数是3，次数是2 B、﹣xy²z的系数是﹣1，次数是4 C、单项式m的次数是1，没有系数 D、多项式2x²+xy+3是四次三项式

查看试题解析
9. 如果 $\frac{1}{3} x^{a + 1} y^{2 a + 3}$ 与 $- 3 x^{2} y^{2 b - 1}$ 是同类项，那么a，b的值分别是（）

A、 $a = 1$ ， $b = 2$ B、 $a = 1$ ， $b = 3$ C、 $a = 2$ ， $b = 3$ D、 $a = 3$ ， $b = 2$

查看试题解析
10. 若 $(3 x^{2} - 3 x + 2) - (- x^{2} + 3 x - 3) = A x^{2} - B x + C$ ，则A，B，C的值分别为（）

A、4，-6，5 B、4，0，-1 C、2，0，5 D、4，6，5

查看试题解析
11. 已知一个多项式与 $3 x^{2} + 9 x$ 的和等于 $5 x^{2} + 4 x - 1$ ，则这个多项式是（）

A、 $8 x^{2} + 13 x - 1$ B、 $- 2 x^{2} + 5 x + 1$ C、 $8 x^{2} - 5 x + 1$ D、 $2 x^{2} - 5 x - 1$

查看试题解析
12. 如图，下列图形都是由同样大小的小四边形按照一定规律所组成的，其中第1个图形中共有4小四边形，第2个图形中共有9个小四边形，第3个图形中共有16个小四边形，…，照此规律排列下去，第n个图形中小四边形的个数为（）

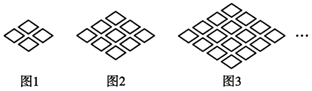A、n²+2 B、n²+2n+1 C、n²+n+1 D、n²+2n

查看试题解析

二、填空题

13. 如果单项式 $- 4 a^{n} b^{2} c$ 是 $6$ 次单项式，那么 $n$ 的值为.

查看试题解析
14. 单项式 $- \frac{3 π a^{2} b}{4}$ 的系数是，次数是 .

查看试题解析
15. 一件羽绒服的原价为a元，商场为了促销决定按七折销售，则这件羽绒服降价后的价格为．

查看试题解析
16. 当 $x = 1$ 时，代数式 $x^{2} - 2 b x + a$ 的值为 $3$ ，则当 $x = - 2$ 时，代数式 $x^{2} + b x + a =$ .

查看试题解析
17. 已知单项式 $a^{m} b^{2}$ 与－ $\frac{2}{3}$ $a^{4} b^{n - 1}$ 的和是单项式，那么 m＝， n＝ .

查看试题解析
18. 按如图所示的计算程序计算，若开始输入的 $x$ 值为2，第一次得到的结果为1，第二次得到的结果为4，……，则第8次得到的结果为.

查看试题解析

三、解答题

19. 先化简，再求值： $3 x^{2} y - [2 x y - 2 (x y - \frac{3}{2} x^{2} y)] + 3 x y^{2}$ ﹣xy，其中x＝3，y＝﹣ $\frac{1}{3}$ .

查看试题解析
20. 先化简，再求值： $(2 x y^{2} + x^{3} y) - [(4 x^{2} y^{2} - x y^{2}) + \frac{1}{2} (- 8 x^{2} y^{2} + 4 x^{3} y)] ，$ 其中 $x = - 1 ， y = \frac{1}{2}$ .

查看试题解析
21. 先化简，再求值： $3 x^{2} y - [2 x y^{2} - 2 (x y - \frac{3}{2} x^{2} y)] + 3 x y^{2} - x y$ ，其中 $x = 1$ ， $y = - 3$ .

查看试题解析
22. 先化简，再求值 $(3 x^{2} - 2 y) - [x^{2} - 2 (x^{2} - x y)]$ ，其中， $x = - \frac{1}{2}$ ， $y = 2$ .

查看试题解析
23. 先化简，再求值.2（3a﹣4b）﹣3（3a+2b）+4（3a﹣2b），其中 $a = - \frac{1}{3}$ ， $b = \frac{1}{2}$ .

查看试题解析
24. 已知实数m使得多项式 $(2 m x^{2} - x^{2} + 3 x + 1) - (5 x^{2} - 4 y^{2} + 3 x)$ 化简后不含 $x^{2}$ 项，求代数式 $2 m^{3} - [2 m^{3} - (4 m - 5) + m]$ 的值.

查看试题解析
25. 已知代数式 $A = a^{4} - 3 a^{2} b^{2} - a b^{3} + 5$ ， $B = 2 b^{4} - 2 a^{2} b^{2} + a b^{3}$ ， $C = a^{4} - 5 a^{2} b^{2} + 2 b^{4} - 2$ .小丽说：“代数式 $A + B - C$ 的值与 $a$ ， $b$ 的值无关.”她说得对吗？说说你的理由.

查看试题解析
26. 探索规律：将连续的偶数2，4，6，8，…，排成如下表：

(1)、图中十字框中的五个偶数的和与中间的偶数16有什么关系？

(2)、移动十字架，设中间的偶数为x，用代数式表示十字框中的五个偶数的和；

(3)、若将十字框上下左右移动，可框住另外的五个偶数，则能框住五个偶数的和等于2010吗？如能写出这五个偶数；如不能，说明理由。

查看试题解析

北师版数学七年级上册《第三章 整式及其加减》单元检测B卷

一、单选题

二、填空题

三、解答题

北师版数学七年级上册《第三章整式及其加减》单元检测B卷