2021-2022学年人教版七年级上册数学期末质量检测卷

试卷更新日期：2021-08-14 类型：期末考试

进入出卷网下载

一、单选题

1. 下列计算正确的是（）

A、3a+4b=7ab B、3a-2a=1 C、 $3 a^{2} b - 2 a b^{2} = a^{2} b$ D、 $2 a^{2} + 3 a^{2} = 5 a^{2}$

查看试题解析
2. 下列各组数中，负数的个数是（）
﹣2，33.2，﹣|﹣ $\frac{1}{4}$ |，0.75，﹣37.5%， $\frac{3}{4}$ ，0，﹣0.6，﹣7．

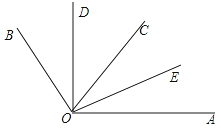
A、1个 B、2个 C、3个 D、5个

查看试题解析
3. 给出下列判断：①单项式5×10³x²y的系数是5；②x﹣2xy+y是二次三项式；③多项式﹣3a²b+7a²b²﹣2ab+1的次数是9；④几个有理数相乘，当负因数有奇数个时，积为负.其中判断正确的是（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
4. 如图是一个正方体纸盒的外表面展开图，则这个正方体是（）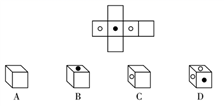

A、A B、B C、C D、D

查看试题解析
5. 据有关部门初步统计，自新冠肺炎疫情发生以来，国家已经投入1390亿资金进行疫情防控，为抗击疫情提供了强力保障，也展现了祖国日益强大的综合国力!将数据1390亿用科学记数法表示为1.390×10ⁿ ，其中n的值为（　　）

A、4 B、10 C、11 D、3

查看试题解析
6. 若2＜x＜3，那么化简|2－x|－|x－3|结果是（）

A、－2x+5 B、2x－5 C、1 D、－5

查看试题解析
7. 如图，OC是∠AOB的平分线，OD平分∠AOC，且 $∠ A O B = 100^{\circ}$ ，则∠COD的度数是（）

A、75° B、50° C、25° D、20°

查看试题解析
8. 如果 $x = 2$ 是关于 $x$ 的方程 $2 x - m + 3 = 0$ 的解，那么 $m$ 的值为（）.

A、-1 B、-7 C、1 D、7

查看试题解析
9. 某种品的标价为120元，若以九折降价出售，相对于进货价仍获利20%，该商品的进货价为（）

A、80元 B、85元 C、90元 D、95元

查看试题解析
10. 根据以下图形变化的规律，图中的省略号里黑色正方形的个数可能是（）

A、2016 B、2017 C、2018 D、2019

查看试题解析

二、填空题

11. 单项式 $- \frac{2}{3} π x y^{2}$ 的次数是次．

查看试题解析
12. 请写出一个解为 $x = - 1$ 的一元一次方程：

查看试题解析
13. 若|a|＝4，b²＝9，且a＜b，那么a﹣b＝.

查看试题解析
14. 已知2x+4与3x﹣2互为相反数，则x=.

查看试题解析
15. 已知 $α = 50 °$ ，则它的余角与补角的度数和等于 $°$ .

查看试题解析
16. 多项式 $x^{2} - 3 m x y - 3 y^{2} + 6 x y - 8$ 中不含 $x y$ 项，则常数 $m$ 的值是.

查看试题解析
17. 如图，C、D是线段AB上两点，若CB=4，DB=7，且D是AC中点，则AC的长等于.

查看试题解析
18. 按下面的程序计算：

若输入 $n = 20$ ，输出结果是101；若开始输入的n值为正整数，最后输出的结果为131，则开始输入的n值可以是.

查看试题解析

三、解答题

19. 计算：

(1)、－3²－3×(－ $\frac{1}{3}$ )²－( $\frac{1}{4}$ + $\frac{1}{3}$ － $\frac{1}{2}$ )×12

(2)、3x²－[5x－( $\frac{1}{2}$ x－3)+2x²]

查看试题解析
20. 解方程

(1)、 $5 (x - 1) = 8 x - 2 (x + 1)$

(2)、 $\frac{2 x + 1}{3} - \frac{5 x - 1}{6} = 1$

查看试题解析
21. 先化简，再求值：2(3xy-x²)-3(xy-2x²)-xy，其中x=- $\frac{1}{2}$ ，y=3.

查看试题解析
22. 如图，O为直线AB上的一点，∠AOC＝50°，OD平分AOC，∠DOE＝90°

①求∠BOD的度数；②OE是∠BOC的平分线吗？为什么？

查看试题解析
23. 小明从家里骑自行车到学校，每小时骑15千米，可早到10分钟；每小时骑12千米，就会迟到5分钟，问他家到学校的路程是多少千米？

查看试题解析
24.
如图，OD平分∠BOC，OE平分∠AOC．若∠BOC=70°，∠AOC=50°．
（1）求出∠AOB及其补角的度数；
（2）请求出∠DOC和∠AOE的度数，并判断∠DOE与∠AOB是否互补，并说明理由．

查看试题解析
25. 已知数轴上，M表示－10，点N在点M的右边，且距M点40个单位长度，点P，点Q是数轴上的动点．

(1)、直接写出点N所对应的数；

(2)、若点P从点M出发，以5个单位长度/秒的速度向右运动，同时点Q从点N出发，以3个单位长度/秒向左运动，设点P、Q在数轴上的D点相遇，求点D的表示的数；

(3)、若点P从点M出发，以5个单位长度/秒的速度向右运动，同时点Q从点N出发，以3个单位长度/秒向右运动，问经过多少秒时，P，Q两点重合？

查看试题解析
26. 如图，阶梯图的每个台阶上都标着一个数，从下到上的第 $1$ 个至第 $4$ 个台阶上依次标着 $- 5 ， - 2 ， 1 ， 9$ ，且任意相邻四个台阶上的数的和都相等．

(1)、求前4个台阶上的数的和；

(2)、求第5个台阶上的数x的值；

(3)、从下到上前 $n (n$ 为奇数)个台阶上的数的和能否为 $2020$ ？若能，求出n的值；若不能，请说明理由．

查看试题解析