初中数学浙教版九年级上册4.6 相似多边形同步练习
试卷更新日期：2021-08-13 类型：同步测试
一、单选题
-
1. 两个相似多边形的一组对应边分别是3cm和4.5cm，如果它们的周长之和是80cm，那么较大的多边形的周长是（ ）A、16cm B、32cm C、48cm D、52cm2. 如图，四边形ABCD∽四边形EFGH，∠A＝80°，∠C＝90°，∠F＝70°，则∠E的度数为（ ）
A、70° B、80° C、90° D、120°3. 把一张矩形的纸片对折后和原矩形相似，那么大矩形与小矩形的相似比是（ ）A、 ：1 B、4：1 C、3：1 D、2：14. 如图所示，在长为8 cm，宽为4 cm的矩形中，截去一个矩形，使得留下的矩形(图中阴影部分)与原矩形相似，则留下矩形的面积是（ ）
A、2 cm2 B、4 cm2 C、8 cm2 D、16 cm25. 如图，矩形相框的外框矩形的长为12dm，宽为8dm，上下边框的宽度都为xdm，左右边框的宽度都为ydm．则符合下列条件的x，y的值能使内边框矩形和外边框矩形相似的为（ ）
A、x=y B、3x=2y C、x=1，y=2 D、x=3，y=26. 两个相似多边形的周长比是3：4，其中小多边形的面积为18cm2 ， 则较大多边形的面积为（ ）．A、16cm2 B、54cm2 C、32cm2 D、48cm27. 一个长方形各边按 扩大后，得到的图形与原图形比较，下列说法中正确的是（ ）A、周长扩大原来的16倍 B、周长缩小原来的 C、面积扩大原来的16倍 D、面积缩小原来的8. 若两个相似多边形的面积之比为 ，则这两个多边形的周长之比为 （ ）A、 B、16：81 C、4：9 D、2：39. 将矩形按照如图所示的方式向外扩张得到新矩形，每条对角线向其延长线两个方向各延伸 ，若所得新矩形与原矩形相似，则a的值的个数可以是（ ）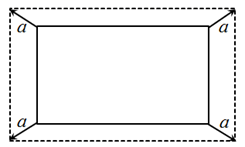
A、1 B、2 C、3 D、无数个10. 如图，在 的小正方形网格中，勤奋学习小组的同学画出了五边形 和五边形 则下列说法中，错误的是（ ）
A、五边形 五边形 B、 C、五边形 的周长是五边形 周长的 倍． D、二、填空题
-
11. 已知矩形ABCD的周长的平方与面积的比为18，则矩形ABCD的较长的一边与较短的一边的长度的比等于.12. 复印纸型号多样，而各型号复印纸之间存在这样的关系：将其中一型号纸张（如A3纸）沿较长边中点的连线对折，就能得到下一型号（A4纸）的纸张，且对折得到的两个矩形和原来的矩形相似（即A3纸与A4纸相似），则这些型号的复印纸宽与长之比为.
13. 若两个相似五边形的相似比为 3:5， 则它们的面积比为14. 如果两个相似多边形面积之比为4：9，则它们的边长之比为 ．15. 如图，方桌正上方的灯泡（看作一个点）发出的光线照射方桌后，在地面上形成阴影（正方形）示意图，已知方桌边长1.2 m，桌面离地面1.2 m，灯泡离地面3.6 m，则地面上阴影部分的面积为 ．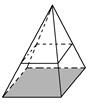
16. 如图所示，复印纸的型号有A0 ， A1 ， A2 ， A3 ， A4等，它们之间存在着这样一种关系：将其中某一型号（如A3）的复印纸沿较长边的中点对折，就能得到两张下一型号（A4）的复印纸，且得到的两个矩形都和原来的矩形相似，那么这些型号的复印纸的长、宽之比为 ．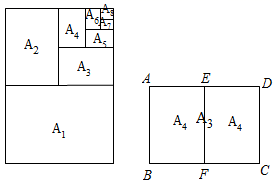
三、解答题
-
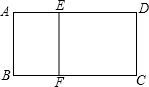
17. 两个相似多边形的最长边分别为6cm和8cm，它们的周长之和为56cm，面积之差为28cm2 ， 求较小相似多边形的周长与面积.18. 如图，矩形ABCD中，AB=4，点E，F分别在AD，BC边上，且EF⊥BC，若矩形ABFE∽矩形DEFC，且相似比为1：2，求AD的长．
19. 如图，一个矩形广场的长为100m，宽为80m，广场外围两条纵向小路的宽均为1.5m，如果两条横向小路的宽都为xm，那么当x为多少时，小路内、外边缘所围成的两个矩形相似.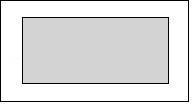
20. 若四边形ABCD与四边形A1B1C1D1相似，相似比为k1= ，又四边形A1B1C1D1与四边形A2B2C2D2相似，相似比为k2= ，请问四边形ABCD与四边形A2B2C2D2相似吗？若相似，相似比是多少？
21. 已知四边形ABCD与四边形A1B1C1D1相似，且A1B1：B1C1：C1D1：D1A1=7：8：11：14，若四边形ABCD的周长为40，求四边形ABCD各边的长．
22. 如图，四边形ABCD和四边形EFGH相似，求∠α、∠β的大小和EH的长度．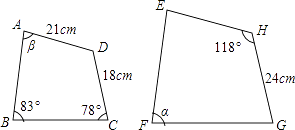
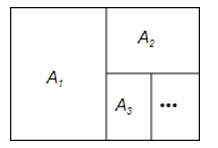
23.如图，An系列矩形纸张的规格特征是：①各矩形纸张都相似；②A1纸对裁后可以得到两张A2纸，A2纸对裁后可以得到两张A3纸，…，An纸对裁后可以得到两张An+1纸．
（1）求：A1纸面积是A2纸面积的多少倍，A2纸周长是A4纸周长的多少倍；
（2）根据An系列纸张的规格特征，求出该系列纸张的长与宽（长大于宽）之比；
（3）设A1纸张的重量为a克，试求出A8纸张的重量．（用含a的代数式表示）
四、综合题
-
24. 阅读下列材料，完成任务：
自相似图形
定义：若某个图形可分割为若干个都与它相似的图形，则称这个图形是自相似图形.例如：正方形ABCD中，点E、F、G、H分别是AB、BC、CD、DA边的中点，连接EG，HF交于点O，易知分割成的四个四边形AEOH、EBFO、OFCG、HOGD均为正方形，且与原正方形相似，故正方形是自相似图形.
任务：
(1)、如图1中正方形ABCD分割成的四个小正方形中，每个正方形与原正方形的相似比为；(2)、如图2，已知△ABC中，∠ACB=90°，AC=4，BC=3，小明发现△ABC也是“自相似图形”，他的思路是：过点C作CD⊥AB于点D，则CD将△ABC分割成2个与它自己相似的小直角三角形.已知△ACD∽△ABC，则△ACD与△ABC的相似比为；(3)、现有一个矩形ABCD是自相似图形，其中长AD=a，宽AB=b（a＞b）.请从下列A、B两题中任选一条作答.
A：①如图3﹣1，若将矩形ABCD纵向分割成两个全等矩形，且与原矩形都相似，则a=（用含b的式子表示）；
②如图3﹣2若将矩形ABCD纵向分割成n个全等矩形，且与原矩形都相似，则a=（用含n，b的式子表示）；
B：①如图4﹣1，若将矩形ABCD先纵向分割出2个全等矩形，再将剩余的部分横向分割成3个全等矩形，且分割得到的矩形与原矩形都相似，则a=（用含b的式子表示）；
②如图4﹣2，若将矩形ABCD先纵向分割出m个全等矩形，再将剩余的部分横向分割成n个全等矩形，且分割得到的矩形与原矩形都相似，则a=（用含m，n，b的式子表示）.