2021-2022学年人教版九年级上册第二十四章 圆 单元测试
试卷更新日期：2021-08-13 类型：单元试卷
一、单选题
-
1. 有下列说法：①等弧的长度相等；②直径是圆中最长的弦；③相等的圆心角对的弧相等；④圆中90°角所对的弦是直径；⑤同圆中等弦所对的圆周角相等．其中正确的有（ ）
A、1个 B、2个 C、3个 D、4个2. 圆心角为60°，半径为1的弧长为（ ）A、π² B、π C、 D、3. 如图，△ABC的顶点A，B，C均在⊙O上，若∠ABC+∠AOC＝75°，则∠OAC的大小是（ ）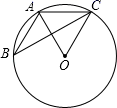
A、25° B、50° C、65° D、75°4. 已知△ABC的外接圆⊙O ， 那么点O是△ABC的（ ）A、三条中线交点 B、三条高的交点 C、三条边的垂直平分线的交点 D、三条角平分线交点5. 如图，每个小正方形的边长为1，格点A、B、C在同一圆弧上，若点A的坐标为(﹣2，3)，则该圆弧所在圆的圆心坐标是（ ）
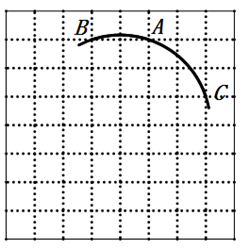A、(﹣1，1) B、(﹣3，0) C、(﹣3，1) D、(0，1)6. 《九章算术》是我国古代著名数学著作，书中记载：“今有圆材，埋在壁中，不知大小以锯锯之，深一寸，锯道长一尺，问径几何？”用数学语言可表述为：“如图，CD为⊙O的直径，弦AB⊥DC于E，ED=1寸，AB=10寸，求直径CD的长。”则CD为（ ）
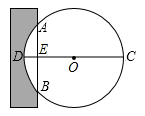A、10寸 B、3寸 C、20寸 D、26寸7. 如图，正六边形ABCDEF内接于于⊙O，连接BD，则∠CBD的度数是（ ）
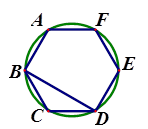A、30° B、45° C、60° D、90°8. 如图，已知等边 的内切圆 半径为3，则 的长为 （ ）
A、 B、 C、 D、9. 如图，已知等边△ABC的边长为8，以AB为直径的圆交BC于点F．以C为圆心，CF长为半径作图，D是⊙C上一动点，E为BD的中点，当AE最大时，BD的长为（ ）
A、 B、 C、 D、1210. 如图，在菱形 中，点 是 的中点，以C为圆心、 为半径作弧，交 于点F，连接 .若 ， ，则阴影部分的面积为（ ）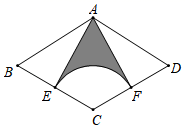
A、 B、 C、 D、二、填空题
-
11. 圆锥的母线长为3，底面圆的半径为2，则这个圆锥的全面积为 ．12. 如图，点A，B，C在⊙O上，∠A=40度，∠C=20度，则∠B=度．
13. 已知 的半径为 ， ，则点P在 的.（填“上面”“内部”或“外部”）14. 把光盘、含 60°角的三角板和直尺如图摆放，AB＝2，则光盘的直径是.
15. 如图，正方形ABCD是⊙O的内接正方形，点P是劣弧 上不同于点B的任意一点，则∠BPC=度．
16. 已知AB是⊙O的直径，弦CD⊥AB于点E，弦PQ∥AB交弦CD于点M，BE=18，CD=PQ=24，则OM的长为.
17. 在平面直角坐标系中，直线y=x-2与x轴、y轴分别交于点B、C，半径为1的⊙P的圆心P从点A（4，m ）出发以每秒 个单位长度的速度沿射线AC的方向运动，设点P运动的时间为t秒，则当t=秒时，⊙P与坐标轴相切.
18. 如图， 是 的直径， ，C为 的三等分点（更靠近A点），点P是 上一个动点，取弦 的中点D，则线段 的最大值为.
三、解答题
-
19. 如图，在圆内接四边形ABCD中，O为圆心，∠BOD=160°，求∠BCD的度数．
20. 如图，已知圆锥底面⊙O的直径BC=6，高AO=4求该圆锥侧面展开图的面积。
21. 已知：如图，AB是⊙O的直径，点C、D在⊙O上，CE⊥AB于E，DF⊥AB于F，且AE=BF，AC与BD相等吗？为什么？
22. 巫山长江公路大桥是一个中承式钢管砼圆弧形拱桥，主跨度AB=492米，拱桥最高点C距水面100米，求该拱桥的半径是多少米？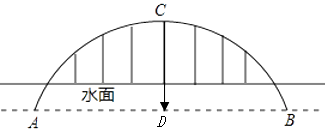
23. AB为⊙O直径，BC为⊙O切线，切点为B，CO平行于弦AD，作直线DC．
①求证：DC为⊙O切线；
②若AD•OC＝8，求⊙O半径r．
24. 如图，已知AB为⊙O的直径，AC是⊙O的弦，D是弧BC的中点，过点D作⊙O的切线，分别交AC、AB的延长线于点E和点F，连接CD、BD．
(1)、求证：∠A＝2∠BDF；(2)、若AC＝3，AB＝5，求CE的长．
