初中数学浙教版九年级上册4.5 相似三角形的性质及应用同步练习
试卷更新日期:2021-08-13 类型:同步测试
一、单选题
-
1. 如图,在 中, , 于点 , , , ,则 的长是( )
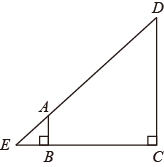 A、14 B、12.4 C、10.5 D、9.32. 如图,已知 .
A、14 B、12.4 C、10.5 D、9.32. 如图,已知 .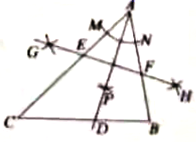
⑴以点A为圆心,以适当长为半径画弧,交 于点M , 交 于点N .
⑵分别以M , N为圆心,以大于 的长为半径画弧,两弧在 的内部相交于点P .
⑶作射线 交 于点D .
⑷分别以A , D为圆心,以大于 的长为半径画弧,两弧相交于G , H两点.
⑸作直线 ,交 , 分别于点E , F .
依据以上作图,若 , , ,则 的长是( )
A、 B、1 C、 D、43. 过△ABC的重心G作GE∥BC交AC于点E,线段BC=12,线段GE长为( )A、4 B、4.5 C、6 D、84. 图1是装了液体的高脚杯示意图(数据如图),用去一部分液体后如图2所示,此时液面 ( )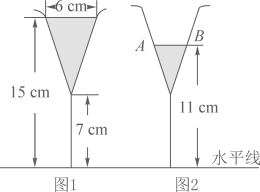 A、 B、 C、 D、5. 如图, ,下列说法错误的是( )
A、 B、 C、 D、5. 如图, ,下列说法错误的是( ) A、两个三角形是位似图形 B、点A是两个三角形的位似中心 C、点B与点 D、点C与点E是对应位似点 D. 是相似比6. 如图, 与 交于点 ,则 ( )
A、两个三角形是位似图形 B、点A是两个三角形的位似中心 C、点B与点 D、点C与点E是对应位似点 D. 是相似比6. 如图, 与 交于点 ,则 ( ) A、2 B、3 C、3.5 D、47. 如图,把 沿着 的方向平移到 的位置,它们重叠部分的面积是 面积的一半,若 ,则 移动的距离是( )
A、2 B、3 C、3.5 D、47. 如图,把 沿着 的方向平移到 的位置,它们重叠部分的面积是 面积的一半,若 ,则 移动的距离是( )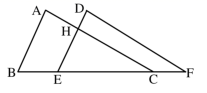 A、 B、 C、 D、8. 小刚身高 ,测得他站立在阳光下的影子长为 ,紧接着他把手臂竖直举起,测得影子长为 ,那么小刚举起的手臂超出头顶( )A、 B、 C、 D、9. 《九章算术》是我国数学经典,上面记载:“今有邑方不知大小,各中开门.出北门三十步有木,出西门七百五十步见木.问邑方几何?”其意思是:如图,已知正方形小城ABCD , 点E , G分别为CD , AD的中点,EF⊥CD , GH⊥AD , 点F , D , H在一条直线上,EF=30步,GH=750步.正方形小城ABCD的边长是( )
A、 B、 C、 D、8. 小刚身高 ,测得他站立在阳光下的影子长为 ,紧接着他把手臂竖直举起,测得影子长为 ,那么小刚举起的手臂超出头顶( )A、 B、 C、 D、9. 《九章算术》是我国数学经典,上面记载:“今有邑方不知大小,各中开门.出北门三十步有木,出西门七百五十步见木.问邑方几何?”其意思是:如图,已知正方形小城ABCD , 点E , G分别为CD , AD的中点,EF⊥CD , GH⊥AD , 点F , D , H在一条直线上,EF=30步,GH=750步.正方形小城ABCD的边长是( ) A、150步 B、200步 C、250步 D、300步10. 如图,在Rt△ABC中,∠ACB=90°,分别以其三边为边向外作正方形,延长EA交BG于点M,连接IM交AB于点N,若M是BG的中点,则 的值为( )
A、150步 B、200步 C、250步 D、300步10. 如图,在Rt△ABC中,∠ACB=90°,分别以其三边为边向外作正方形,延长EA交BG于点M,连接IM交AB于点N,若M是BG的中点,则 的值为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 如图,为了测量山坡的护坡石坝高,把一根长为 的竹竿 斜靠在石坝旁,量出竿上 长为 时,它离地面的高度 为 ,则坝高 为 .
 12. 已知点D与点A(0,6)、B(0,﹣4)、C(x , y)是平行四边形的四个顶点,其中x、y满3x﹣4y+12=0,则CD的最小值为 .13. 学校门口的栏杆如图所示,栏杆从水平位置B绕点O旋转到AC位置,已知AB⊥BD,CD⊥BD,垂足分别为B,D,AO=4m,AB=1.6m,CO=1m,则栏杆C端应下降的垂直距离CD为
12. 已知点D与点A(0,6)、B(0,﹣4)、C(x , y)是平行四边形的四个顶点,其中x、y满3x﹣4y+12=0,则CD的最小值为 .13. 学校门口的栏杆如图所示,栏杆从水平位置B绕点O旋转到AC位置,已知AB⊥BD,CD⊥BD,垂足分别为B,D,AO=4m,AB=1.6m,CO=1m,则栏杆C端应下降的垂直距离CD为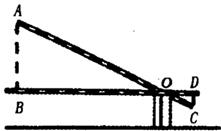 14. 如图,正方形纸片ABCD的边长为12,点F是AD上一点,将 沿CF折叠,点D落在点G处,连接DG并延长交AB于点E . 若 ,则GE的长为 .
14. 如图,正方形纸片ABCD的边长为12,点F是AD上一点,将 沿CF折叠,点D落在点G处,连接DG并延长交AB于点E . 若 ,则GE的长为 . 15. 如图,在 中, ,过点B作 ,垂足为B , 且 ,连接CD , 与AB相交于点M , 过点M作 ,垂足为N . 若 ,则MN的长为 .
15. 如图,在 中, ,过点B作 ,垂足为B , 且 ,连接CD , 与AB相交于点M , 过点M作 ,垂足为N . 若 ,则MN的长为 .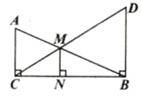 16. 如图, 中,G为重心, ,那么 =;
16. 如图, 中,G为重心, ,那么 =;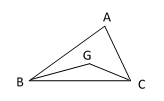
三、解答题
-
17. 如图,利用标杆 测量楼高,点A,D,B在同一直线上, , ,垂足分别为E,C.若测得 , , ,楼高 是多少?
 18. 如图,强强同学为了测量学校一棵笔直的大树OE的高度,先在操场上点A处放一面平面镜,从点A处后退1m到点B处,恰好在平面镜中看到树的顶部E点的像;再将平面镜向后移动4m(即AC=4m)放在C处,从点C处向后退1.5m到点D处,恰好再次在平面镜中看到大树的顶部E点的像,测得强强的眼睛距地面的高度FB、GD为1.5m,已知点O,A,B,C,D在同一水平线上,且GD⊥OD,FB⊥OD,EO⊥OD.求大树OE的高度.(平面镜的大小忽略不计)
18. 如图,强强同学为了测量学校一棵笔直的大树OE的高度,先在操场上点A处放一面平面镜,从点A处后退1m到点B处,恰好在平面镜中看到树的顶部E点的像;再将平面镜向后移动4m(即AC=4m)放在C处,从点C处向后退1.5m到点D处,恰好再次在平面镜中看到大树的顶部E点的像,测得强强的眼睛距地面的高度FB、GD为1.5m,已知点O,A,B,C,D在同一水平线上,且GD⊥OD,FB⊥OD,EO⊥OD.求大树OE的高度.(平面镜的大小忽略不计) 19. 九年级活动小组计划利用所学的知识测量操场旗杆高度.测量方案如下:如图,小卓在小越和旗杆之间的直线BM上平放一平面镜,在镜面上做了一个标记,这个标记在直线BM上的对应位置为点C,镜子不动,小卓看着镜面上的标记,他来回走动,走到点D时看到旗杆顶端点A在镜面中的像与镜面上的标记点C重合,这时测得小卓眼睛与地面的高度ED=1.5米,CD=1米,然后在阳光下,小越从D点沿DM方向走了15.8米到达F处此时旗杆的影子顶端与小越的影子顶端恰好重合,测得FG=1.6米,FH=3.2米,已知AB⊥BM,ED⊥BM,GF⊥BM若测量时所使用的平面镜的厚度忽略不计,请你根据图中提供的相关信息求出旗杆的高AB.
19. 九年级活动小组计划利用所学的知识测量操场旗杆高度.测量方案如下:如图,小卓在小越和旗杆之间的直线BM上平放一平面镜,在镜面上做了一个标记,这个标记在直线BM上的对应位置为点C,镜子不动,小卓看着镜面上的标记,他来回走动,走到点D时看到旗杆顶端点A在镜面中的像与镜面上的标记点C重合,这时测得小卓眼睛与地面的高度ED=1.5米,CD=1米,然后在阳光下,小越从D点沿DM方向走了15.8米到达F处此时旗杆的影子顶端与小越的影子顶端恰好重合,测得FG=1.6米,FH=3.2米,已知AB⊥BM,ED⊥BM,GF⊥BM若测量时所使用的平面镜的厚度忽略不计,请你根据图中提供的相关信息求出旗杆的高AB. 20. 某校数学实践社团开展了一次“利用数学知识测量学校操场上旗杆高度”的实践活动,该校九年级学生积极参与.小红和小华决定利用下午课间的时间,用测量影长的方式求出旗杆高度.同一时刻测量站在旗杆旁边的小红(CD)和旗杆AB的影长时,发现旗杆的影子一部分落在地面上(BF),另一部分落在了距离旗杆24m的教学楼上(EF).经测量,小红落在地面上的影长DG为2.4m,教学楼上的影长EF为2m.已知小红的身高是1.6m,请根据小红和小华的测量结果,求出旗杆AB的高度.
20. 某校数学实践社团开展了一次“利用数学知识测量学校操场上旗杆高度”的实践活动,该校九年级学生积极参与.小红和小华决定利用下午课间的时间,用测量影长的方式求出旗杆高度.同一时刻测量站在旗杆旁边的小红(CD)和旗杆AB的影长时,发现旗杆的影子一部分落在地面上(BF),另一部分落在了距离旗杆24m的教学楼上(EF).经测量,小红落在地面上的影长DG为2.4m,教学楼上的影长EF为2m.已知小红的身高是1.6m,请根据小红和小华的测量结果,求出旗杆AB的高度. 21. 已知:在 中,点D、E分别在AC、AB上,且满足 ,求证: .
21. 已知:在 中,点D、E分别在AC、AB上,且满足 ,求证: .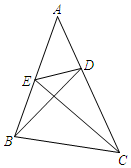 22. 如图所示是测量河宽的示意图,AE与BC相交于点D,AB⊥BC于点B,CE⊥BC于点C,测得BD=150m,DC=75m,EC=60m,求河宽AB.
22. 如图所示是测量河宽的示意图,AE与BC相交于点D,AB⊥BC于点B,CE⊥BC于点C,测得BD=150m,DC=75m,EC=60m,求河宽AB.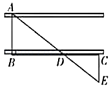 23. 王老师要装修自己带阁楼的新居(下图为新居剖面图),在建造客厅到阁楼的楼梯 时,为避免上楼时墙角 碰头,设计墙角 到楼梯的竖直距离 为 ,他量得客厅高 ,楼梯洞口宽 ,阁楼阳台宽 .请你帮助王老师解决问题:要使墙角 到楼梯的竖直距离 为 ,楼梯底端 到墙角 的距离 是多少米?
23. 王老师要装修自己带阁楼的新居(下图为新居剖面图),在建造客厅到阁楼的楼梯 时,为避免上楼时墙角 碰头,设计墙角 到楼梯的竖直距离 为 ,他量得客厅高 ,楼梯洞口宽 ,阁楼阳台宽 .请你帮助王老师解决问题:要使墙角 到楼梯的竖直距离 为 ,楼梯底端 到墙角 的距离 是多少米?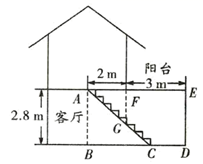
四、综合题
-
24. 问题背景:
 (1)、如图1,在 中, , 于D,求证: ;(2)、如图2,在 中, ,点E为 中点, 于D, 交 于F,若 ,求 的值;(3)、如图3,在 中, ,点E为 中点, 于D, 交 于F,若 ,直接写出 的值.
(1)、如图1,在 中, , 于D,求证: ;(2)、如图2,在 中, ,点E为 中点, 于D, 交 于F,若 ,求 的值;(3)、如图3,在 中, ,点E为 中点, 于D, 交 于F,若 ,直接写出 的值.