初中数学浙教版九年级上册4.4 两个三角形相似的判定同步练习
试卷更新日期:2021-08-13 类型:同步测试
一、单选题
-
1. 能判定 与 相似的条件是( )A、 B、 ,且 C、 且 D、 ,且2. 如图,已知△ABC,则下列4个三角形中,与△ABC相似的是( )
 A、
A、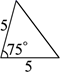 B、
B、 C、
C、 D、
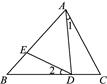
D、 3. 如图,在△ABC中,∠BAC=90°,F是BA延长线上一点,FD⊥BC于D,交AC于点E,则图中相似三角形共有几对( )
3. 如图,在△ABC中,∠BAC=90°,F是BA延长线上一点,FD⊥BC于D,交AC于点E,则图中相似三角形共有几对( ) A、6对 B、5对 C、4对 D、3对4. 如图,∠1=∠2,要使△ABC∽△ADE , 只需要添加一个条件即可,这个条件不可能是( )
A、6对 B、5对 C、4对 D、3对4. 如图,∠1=∠2,要使△ABC∽△ADE , 只需要添加一个条件即可,这个条件不可能是( )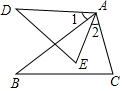 A、∠B=∠D B、∠C=∠E C、 D、5. 如图1,图2,根据图中所标注的数据,能够推得三角形①与②相似的是( )
A、∠B=∠D B、∠C=∠E C、 D、5. 如图1,图2,根据图中所标注的数据,能够推得三角形①与②相似的是( ) A、都相似 B、都不相似 C、只有图1相似 D、只有图2相似6. 如图,在△ABC中,点D、E分别在边AB、AC上,下列条件中不能判断△ABC~△AED的是( )
A、都相似 B、都不相似 C、只有图1相似 D、只有图2相似6. 如图,在△ABC中,点D、E分别在边AB、AC上,下列条件中不能判断△ABC~△AED的是( )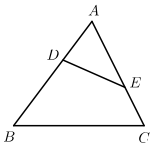 A、∠AED=∠B B、∠ADE=∠C C、 D、7. 如图正方形网格上的三角形(1)(2)(3)中与△ABC相似的是( )
A、∠AED=∠B B、∠ADE=∠C C、 D、7. 如图正方形网格上的三角形(1)(2)(3)中与△ABC相似的是( ) A、(1) B、(2) C、(3) D、都不与△ABC相似8. 如图,在 中,点D、E分别在边 、 上,下列条件中能判断 的是( )
A、(1) B、(2) C、(3) D、都不与△ABC相似8. 如图,在 中,点D、E分别在边 、 上,下列条件中能判断 的是( )① ;② ;③ ;④ .
 A、①② B、①②③ C、①②④ D、①②③④9. 如图,在△ABC中,点D,E分别在边AB、AC上,下列条件中不能判断△ABC∽△ADE的是( )
A、①② B、①②③ C、①②④ D、①②③④9. 如图,在△ABC中,点D,E分别在边AB、AC上,下列条件中不能判断△ABC∽△ADE的是( ) A、∠ADE=∠B B、∠AED=∠C C、 D、10. 如图,在△ABC中,点D , E分别在边AC , BC上,则不一定能判断△ABC∽△EDC的是( )
A、∠ADE=∠B B、∠AED=∠C C、 D、10. 如图,在△ABC中,点D , E分别在边AC , BC上,则不一定能判断△ABC∽△EDC的是( ) A、∠CDE=∠B B、∠DEC=∠A C、 D、
A、∠CDE=∠B B、∠DEC=∠A C、 D、二、填空题
-
11. 如图, , ,则图中相似三角形有对.
 12. 如图, 中, ,点D是边 上的一个动点(点D与点 不重合),若再增加一个条件,就能使 与 相似,则这个条件可以是(写出一个即可).
12. 如图, 中, ,点D是边 上的一个动点(点D与点 不重合),若再增加一个条件,就能使 与 相似,则这个条件可以是(写出一个即可). 13. 如图,在正方形网格中有3个斜三角形:① ;② ;③ ;其中能与 相似的是 . ( 除外)
13. 如图,在正方形网格中有3个斜三角形:① ;② ;③ ;其中能与 相似的是 . ( 除外) 14. 在 中, ,点P为 中点,经过点P的直线截 ,使截得的三角形与 相似,这样的直线共有条.15. 如图,在△ABC中,点E,F分别在AB,AC上,若△AEF∽△ABC,则需要增加的一个条件是(写出一个即可)
14. 在 中, ,点P为 中点,经过点P的直线截 ,使截得的三角形与 相似,这样的直线共有条.15. 如图,在△ABC中,点E,F分别在AB,AC上,若△AEF∽△ABC,则需要增加的一个条件是(写出一个即可) 16. 在直角△ABC中,∠C=90°,CD⊥AB,由∽ , 可得AC2=AD·AB.
16. 在直角△ABC中,∠C=90°,CD⊥AB,由∽ , 可得AC2=AD·AB.
三、解答题
-
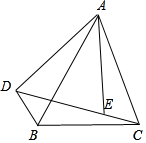
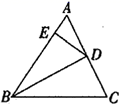
17. 如图,在△ABC中,BD平分∠ABC,交AC于点D,点E是AB上一点,连接DE,BD2=BC·BE.
证明:△BCD∽△BDE.
 18. 如图,点D在△ABC的边AB上,AC2=AD•AB , 求证:△ACD∽△ABC .
18. 如图,点D在△ABC的边AB上,AC2=AD•AB , 求证:△ACD∽△ABC . 19. 如图,D是△ABC的BC边上一点,E为AD上一点,若∠DAC=∠B,CD=CE,试说明△ACE∽△BAD.
19. 如图,D是△ABC的BC边上一点,E为AD上一点,若∠DAC=∠B,CD=CE,试说明△ACE∽△BAD. 20. 如图,在△PAB中,点C、D在AB上,PC=PD=CD,∠A =∠BPD,△APC与△BPD相似吗?为什么?
20. 如图,在△PAB中,点C、D在AB上,PC=PD=CD,∠A =∠BPD,△APC与△BPD相似吗?为什么? 21. 如图, 是矩形 中 边的中点, 交 于点 ,若 的面积为2,求 的面积.
21. 如图, 是矩形 中 边的中点, 交 于点 ,若 的面积为2,求 的面积.