初中数学浙教版九年级上册4.3 相似三角形同步练习

试卷更新日期：2021-08-13 类型：同步测试

进入出卷网下载

一、单选题

1. 如图，已知 $△ A B C$ ∽ $△ A C D$ ，则下列哪条线段与 $A D$ 的比等于相似比（）.

A、 $B D$ B、 $B C$ C、 $A C$ D、 $A B$

查看试题解析
2. 如图，赵师傅透过平举的放大镜从正上方看水平桌面上的菱形图案的一角，那么∠A与放大镜中的∠C的大小关系是（）

A、∠A＝∠C B、∠A>∠C C、∠A<∠C D、无法比较

查看试题解析
3. 若两个相似三角形的面积之比为1∶9，则它们对应角平分线之比为（）

A、 $\frac{1}{3}$ B、3 C、 $\frac{\sqrt{3}}{3}$ D、 $3 \sqrt{3}$

查看试题解析
4. 已知 $△ A B C ∽ △ D E F$ ，点C对应点F，若 $∠ A = 30 °$ ， $∠ B = 75 °$ ，则 $∠ F =$ （）

A、 $30 °$ B、 $75 °$ C、 $95 °$ D、 $105 °$

查看试题解析
5. 已知 $△ A B C ∽ △ D E F$ ，相似比为 $2 ： 1$ ，则 $△ A B C$ 与 $△ D E F$ 的面积比为（）

A、 $4 ： 1$ B、 $2 ： 1$ C、 $1 ： 2$ D、 $1 ： 4$

查看试题解析
6. 如图，已知， $Δ A B C$ 和 $Δ A' B' C'$ 是位似图形，点 $О$ 是位似中心， $A A' = 2 O A ，$ 若 $Δ A B C$ 的面积为2，则 $Δ A' B' C'$ 的面积为（）

A、4 B、8 C、12 D、18

查看试题解析
7. 如图，已知△ABC∽△BDC，其中AC=4，CD=2，则BC=（）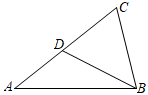

A、2 B、 $2 \sqrt{2}$ C、 $2 \sqrt{3}$ D、4

查看试题解析
8. 如图，在 $Δ A B C$ 中，已知 $\frac{A D}{A B} = \frac{1}{3}$ ，E，F分别在边AC，AB上，DE//BC，DF//AC，则（）

A、 $\frac{D E}{B C} = \frac{1}{4}$ B、 $\frac{D F}{A C} = \frac{1}{3}$ C、 $\frac{S_{Δ D B F}}{S_{Δ A D E}} = 2$ D、 $\frac{S_{Δ D B F}}{S_{四边形 E D F C}} = 1$

查看试题解析
9. 如图，已知△ACD∽△ADB，AC＝4，AD＝2，则AB的长为（）

A、1 B、2 C、3 D、4

查看试题解析
10. 一个三角形框架模型的三边长分别为20厘米、30厘米、40厘米，木工要以一根长为60厘米的木条为一边，做一个与模型三角形相似的三角形，那么另两条边的木条长度不符合条件的是（）

A、30厘米、45厘米 B、40厘米、80厘米 C、80厘米、120厘米 D、90厘米、120厘米

查看试题解析

二、填空题

11. 已知 $△ A B C ∽ △ D E F$ ，它们的周长分别为 $3$ 和 $1$ ，则 $△ A B C$ 与 $△ D E F$ 面积之比为.

查看试题解析
12. 如果两个相似三角形的面积比为4：9，较小三角形的周长为4，那么这两个三角形的周长和为.

查看试题解析
13. 如果两个相似三角形对应边上的中线之比为5：4.那么这两个三角形的周长之比为.

查看试题解析
14. 如图，在Rt△ABC中，∠C＝90°，以顶点A为圆心，适当长为半径画弧，分别交AB，AC于点N，M，再分别以点M，N为圆心，大于MN长为半径画弧，两弧交于点P，射线AP交边BC于点D，若△DAC∽△ABC，则∠B＝度．

查看试题解析
15. 如图， $B D$ 平分 $∠ A B C ，$ 且 $A B = 2 ， B C = 3$ ，则当 $B D =$ 时， $Δ A B D \sim Δ D B C$ .

查看试题解析
16. 如图，在△ABC中，AB=8，AC=6，点D在AC上，且AD=2，如果要在AB上找一点E，使△ADE与△ABC相似，那么AE=。

查看试题解析

三、解答题

17. 如图，正方形ABCD的边长为2，AE=EB，MN=1，线段MN的两端在BC、CD上，若△ADE∽△CMN，求CM的长．

查看试题解析
18. 如图，已知在△ABC中，AB= $\sqrt{5}$ ，AC=2 $\sqrt{5}$ ，BC=3，点M为AB的中点，在线段AC上取点N，使△AMN与△ABC相似，求线段MN的长.

查看试题解析
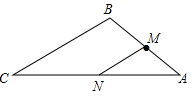19. 如图，在△ABC中，AC＝8厘米，BC＝16厘米，点P从点A出发，沿着AC边向点C以1cm/s的速度运动，点Q从点C出发，沿着CB边向点B以2cm/s的速度运动，如果P与Q同时出发，经过几秒△PQC和△ABC相似？

查看试题解析
20. 如图，已知矩形ABCD的边长 $A B = 3 c m$ ， $B C = 6 c m$ 。某一时刻，动点M从A点出发沿AB方向以 $1 cm / s$ 的速度向B点匀速运动；同时，动点N从D点出发沿DA方向以2cm/s的速度向A点匀速运动，问：是否存在时刻t，使以A，M，N为顶点的三角形与△ACD相似？若存在，求t的值；若不存在，请说明理由。

查看试题解析
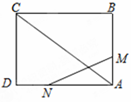21. 已知 $Δ A B C$ 和 $Δ D E F$ 中，有 $\frac{A B}{D E} = \frac{B C}{E F} = \frac{C A}{F D} = \frac{2}{3}$ ,且 $Δ A B C$ 和 $Δ D E F$ 的周长之差为15厘米，求 $Δ A B C$ 和 $Δ D E F$ 的周长.

查看试题解析
22. 已知：CD为一幢3米高的温室，其南面窗户的底框G距地面1米，CD在地面上留下的最大影长CF为2米，现欲在距C点7米的正南方A点处建一幢12米高的楼房AB（设A，C，F在同一水平线上）．

(1)、按比例较精确地作出高楼AB及它的最大影长AE；

(2)、问若大楼AB建成后是否影响温室CD的采光，试说明理由．

查看试题解析
23. 如图，已知△AOB∽△DOC，OA=2，AD=9，OB=5，DC=12．求AB，OC的长．

查看试题解析

四、综合题

24. 【操作、填空】如图， $▱$ ABCD中，对角线AC=a，点E是边AB上一动点，连接DE交AC于点M。

(1)、若AE=BE，则AM的长为；（用含a的式子表示，下同）

(2)、若AE=2BE，则AM的长为；

(3)、若AE=3BE，则AM的长为；

查看试题解析