浙江省金华市浦江县2020-2021学年八年级下学期数学期末考试试卷

试卷更新日期：2021-08-13 类型：期末考试

进入出卷网下载

一、选择题（本题有10小题，每题2分，共20分）

1. （ $\sqrt{5}$ ）²＝（）

A、5 B、 $\sqrt{5}$ C、10 D、 $\sqrt{10}$

查看试题解析
2. 在下列方程中，属于一元二次方程的是（）

A、x²+x³﹣4＝0 B、3（x+1）﹣x＝0 C、x²﹣2＝3x D、x²+3x＝ $\frac{2}{x}$

查看试题解析
3. 小明最近5次数学测验的成绩如下：78，82，79，80，81．则这5次成绩的方差为（）

A、4 B、3 C、2 D、1

查看试题解析
4. 如图，在四边形ABCD中，∠C＝110°，与∠BAD ， ∠ABC相邻的外角都是110°，则∠ADC的外角α的度数是（）

A、90° B、85° C、80° D、70°

查看试题解析
5. 已知点A（﹣2，y₁），B（﹣1，y₂），C（3，y₃）都在比例函数y＝﹣ $\frac{4}{x}$ 图象上，则（）

A、y₁＜y₂＜y₃ B、y₃＜y₁＜y₂ C、y₂＜y₁＜y₃ D、y₃＜y₂＜y₁

查看试题解析
6. 正方形具有而菱形不一定有的性质是（）

A、四条边相等 B、对角线互相垂直平分 C、对角线相等 D、对角线平分一组对角

查看试题解析
7. 用配方法解方程：2x²+4x﹣3＝0，则配方结果正确的是（）

A、（x+1）²＝ $\frac{5}{2}$ B、（x﹣1）²＝ $\frac{5}{2}$ C、（x+1）²＝ $\frac{3}{2}$ D、（x﹣1）²＝ $\frac{3}{2}$

查看试题解析
8. 如图，反比例函数y₁＝ $\frac{k_{1}}{x}$ 的图象和正比例函数y₂＝k₂x的图象交于点A（﹣1，﹣2），B（1，2），若y₁＞y₂ ，则x的取值范围是（）

A、﹣1＜x＜0 B、﹣1＜x＜1 C、x＜﹣1或0＜x＜1 D、﹣1＜x＜0或x＞1

查看试题解析
9. 如图，已知抛物线顶点M在y轴上，抛物线与直线y＝x+1相交于A、B两点．点A在x轴上，点B的横坐标为2，那么抛物线顶点M的坐标是（）

A、（﹣1，0） B、（1，0） C、（0，1） D、（0，﹣1）

查看试题解析
10. 如图，在正方形ABCD中，点E、F分别在边BC、CD上，AE⊥BF ，交点为G ， CH⊥BF ，交BF于点H ．若CH＝HG ， S_△_CFH＝1，那么正方形的面积为（）

A、15 B、20 C、22 D、24

查看试题解析

二、填空题（本题有6小题，每小题3分，共18分）

11. 二次根式 $\sqrt{a + 4}$ 中，字母a的取值范围是．

查看试题解析
12. 菱形的周长为12cm ，它的一个内角为60°，则菱形的面积为（cm²）．

查看试题解析
13. 如图，在▱ABCD中，AC为对角线，BE⊥AC ， DF⊥AC ，垂足分别为点E ， F ．若∠ACB＝45°，AE＝1，BE＝4，则BF＝．

查看试题解析
14. 把面积为5m²的一张纸分割成如图所示的正方形和长方形两部分，设正方形的边长为x（m），则列出的方程化为一般形式是．

查看试题解析
15. 如图，点A ， D在反比例函数y＝ $\frac{k}{x}$ 的图象上，AB ， CD都与y轴垂直，分别交y轴于点B ， C ．已知点A的坐标（1，m），BC＝ $\frac{5}{2}$ ，CD＝ $\frac{8}{3}$ ，则该反比例函数表达式是．

查看试题解析
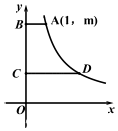16. 如图，矩形ABCD的四个顶点都在正三角形EFG的边上．已知△EFG的边长为6，记矩形ABCD的面积为S ，则当AB＝时，S有最大值是．

查看试题解析

三、解答题（本题有8小题，共62分）

17. 化简：

(1)、 $\sqrt{8}$ × $\sqrt{18}$ ；

(2)、（3﹣ $\sqrt{3}$ ）（ $\sqrt{3}$ +1）．

查看试题解析
18. 解下列方程：

(1)、x²﹣4x﹣5＝0；

(2)、x²﹣7x+1＝0（用公式法解）．

查看试题解析

19. 某校组织“党史知识”学习比赛活动，每班参加比赛的人数相同，成绩分为A、B、C、D四个等级，其中相应等级的得分依次记为100分，90分，80分，70分．学校将八年级一班和二班的学习比赛活动的成绩整理并绘制成如下的统计图．根据以上信息，解答下列问题：

(1)、二班比赛成绩D级人数是人．

(2)、将下面表格补充完整：

班级成绩	平均数	中位数	众数
一班	88.75		100
二班		90	100

查看试题解析

20. 已知抛物线：y＝x²﹣2x﹣3，抛物线图象与x轴交于A ， B两点（点B在点A的右边）．

(1)、求AB两点间的距离及抛物线的顶点坐标．

(2)、若将该抛物线沿垂直方向向上平移1个单位，再沿水平方向向右平移若干个单位后，新的抛物线刚好经过点B ．求平移后新的抛物线表达式．

查看试题解析
21. 如图，将矩形纸ABCD的四个角向内折起，恰好拼成一个无缝隙、无重叠的四边形EFGH ．

(1)、求证：四边形EFGH是矩形；

(2)、若EH＝6cm ， EF＝8cm ，求边AD的长．

查看试题解析
22. 篮球运动员投篮后，球运动的路线为抛物线的一部分（如图），抛物线的对称轴为直线x＝2.5．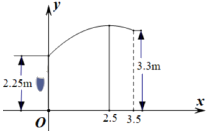

(1)、求篮球运动路线的抛物线表达式和篮球在运动中离地面的最大高度．

(2)、若篮筐离地面3.05m ，离运动员投篮处水平距离为4.2m ，问：篮球以该运动方式，能否投进篮筐？若能投进篮筐，请说明理由；若不能，则运动员应向前还是往后移动多少米后再投篮，刚好能使篮球投进篮筐？

查看试题解析
23. 如图所示，▱ABCD的边AB在x轴上，点D在y轴上，已知OA＝3，AD＝6，BD⊥AD ，从C点出发的点E ，以每秒1个单位的速度向点D移动．M是BD的中点，EM的延长线交AB于点F ．

(1)、求点B ， C的坐标；

(2)、当四边形EFBC是平行四边形时，求点E的移动时间t（秒）．

(3)、当△DEM为等腰三角形时，求CE的长．

查看试题解析
24. 已知点A在反比例函数y＝ $\frac{k}{x}$ （k＞0，x＞0）的图像上，Rt△OAC在平面直角坐标系中的位置如图所示，直角边AC⊥x轴，交x轴于点，把Rt△OAC绕AC中点M逆时针旋转180°，得到△BCA ，四边形OABC的面积为4 $\sqrt{3}$ ，边BC与反比例函数y＝ $\frac{k}{x}$ （k＞0，x＞0）图象交于点E ．

(1)、求该反比例函数的表达式．

(2)、当∠AOC＝60°时，求点E的坐标．

(3)、若直线y＝mx+2与y＝ $\frac{k}{x}$ （k＞0，x＞0）有2个交点．求m的取值范围。

查看试题解析

四、选择题：（本题有两小题，每小题2分，共4分）

25. 已知xy≠1，且3x²+2021x+6＝0，6y²+2021y+3＝0，则 $\frac{y}{x}$ ＝（）

A、 $\frac{1}{2}$ B、2 C、3 D、9

查看试题解析
26. 如图，已知点A₁、A₂、A₃都在反比例函数y＝ $\frac{\sqrt{3}}{x}$ 的图象上，点B₁、B₂、B₃都在x轴上，△OA₁B₁ ， △B₁A₂B₂ ， △B₂A₃B₃都是等边三角形，则点B₃的坐标为（）

A、（2 $\sqrt{3}$ ，0） B、（3 $\sqrt{3}$ ，0） C、（2 $\sqrt{5}$ ，0） D、（3 $\sqrt{5}$ ，0）

查看试题解析

五、填空题：（本题有两小题，每小题3分，共6分）

27. △OAB在直角坐标系中位置如图所示，边OB在x轴上，点C是AB的中点，反比例函数y＝ $\frac{k}{x}$ （k＞0，x＞0）的图象经过A、C两点，设△OAB的面积为6，则k＝．

查看试题解析
28. 如图，二次函数y＝ax²+bx+c的图象经过点A（﹣1，0），B（3，0）．有下列结论：①图象的对称轴为直线：x＝1；②a：b：c＝﹣1：2：3；③若0＜x＜4，则5a＜y＜﹣3a；④一元二次方程cx²+bx+a＝0的两个根分别为﹣1和 $\frac{1}{3}$ ，其中正确的结论有（填序号）．

查看试题解析

六、解答题：（本题有两小题，每小题5分，共10分）

29. 某超市销售一种国产品牌台灯，平均每天可售出100盏，每盏台灯的利润为12元．为了扩大销售，增加利润，超市准备适当降价，据调查，每盏台灯每降价1元，平均每天会多售出20盏．若要实现每天销售获利1400元，则每盏台灯降价多少元？

查看试题解析
30. 如图，矩形ABCD的边AB＝6，AD＝9，点E ， F分别是边AB ， AD上的动点．把△AEF沿直线EF折叠，在同一平面上得到△GEF ，点G为点A的对应点．

(1)、当点F与点D重合时，求BG的最小值；

(2)、当点G落在边BC上的 $\frac{1}{3}$ 处时，求BE长．

查看试题解析