重庆市綦江区2020-2021学年七年级下学期数学期中考试试卷

试卷更新日期：2021-08-13 类型：期中考试

进入出卷网下载

一、选择题：（本大题共12个小题，每小题4分，共48分）在每个小题的下面，都给出了代号为A、B、C、D的四个答案，其中只有一个是正确的，请将答题卡上题号右侧正确答案所对应的方框涂黑。

1. $\frac{1}{4}$ 的平方根是（）

A、 $\frac{1}{2}$ B、- $\frac{1}{2}$ C、 $\pm \frac{1}{2}$ D、 $\frac{1}{16}$

查看试题解析
2. 下列各数： $\sqrt{9}$ 、 $\frac{22}{7}$ 、π、 $\sqrt[3]{- 27}$ ，其中无理数是（　　）

A、 $\sqrt{9}$ B、 $\frac{22}{7}$ C、π D、 $\sqrt[3]{- 27}$

查看试题解析
3. 如图，∠1＝20°，∠AOC＝90°，点B，O，D在同一条直线上，则∠2的度数为（　　）

A、95° B、100° C、110° D、120°

查看试题解析
4. 如图所示，下列条件中，能判断直线l₁∥l₂的是（）

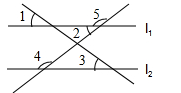A、∠2＝∠3 B、∠1＝∠3 C、∠4+∠5＝180° D、∠2＝∠4

查看试题解析
5. 如图，把一块含有45°角的直角三角板的两个顶点放在直尺的对边上.如果∠1＝15°，则∠2的度数是（　　）

A、30° B、25° C、35° D、20°

查看试题解析
6. 如图，小手盖住的点的坐标可能是（　　）

A、（6，﹣4） B、（5，2） C、（﹣3，﹣6） D、（﹣3，4）

查看试题解析
7. 下列运算正确的是（　　）

A、 $\sqrt{4}$ = $\pm$ 2 B、（﹣3）³=27 C、 $\sqrt{4}$ =2 D、 $\sqrt[3]{9}$ =3

查看试题解析
8. 估计 $\sqrt{76}$ 的值在哪两个整数之间（）

A、75和77 B、6和7 C、7和8 D、8和9

查看试题解析
9. 点A在x轴的下方，y轴的右侧，到x轴的距离是3，到y轴的距离是2，则点A的坐标是（）

A、（2，﹣3） B、（2，3） C、（3，﹣2） D、（﹣3，﹣2）

查看试题解析
10. 用棋子摆出下列一组“口”字，按照这种方法摆下去，则摆第13个“口”字需用棋子（　　）

A、48枚 B、44枚 C、52枚 D、56枚

查看试题解析
11. 如图，将Rt△ABC沿着点B到C的方向平移到△DEF的位置，AB＝10，DO＝4，平移距离为6，则阴影部分面积为（　　）

A、42 B、96 C、84 D、48

查看试题解析
12. 如图，AB⊥BC，AE平分∠BAD交BC于点E，AE⊥DE，∠1+∠2＝90°，M、N分别是BA、CD延长线上的点，∠EAM和∠EDN的平分线交于点F.∠F的度数为（　　）

A、120° B、135° C、150° D、不能确定

查看试题解析

二、填空题：（本大题6个小题，每小题4分，共24分）请将每小题的答案直接填在答题卡中对应的横线上。

13. 如果用（7，8）表示七年级八班，那么八年级七班可表示成．

查看试题解析
14. 一个正数x的平方根是2a﹣3与5﹣a，则a＝.

查看试题解析
15. 若 $\sqrt{a- 3}$ +（b+2）²＝0，则点A（a，b）在象限.

查看试题解析
16. 如图，直线AB∥CD∥EF，且∠B＝40°，∠C＝125°，则∠CGB＝.

查看试题解析
17. 如图所示，直线BC经过原点O，点A在x轴上，AD⊥BC于D，若B（m，3），C（n，﹣5），A（4，0），则AD•BC＝.

查看试题解析
18. 平面内有A、B、C三点，小明同学以A为原点、正东方向为x轴正半轴、正北方向为y轴正半轴、1cm长为单位长度，建立直角坐标系得到B、C两点的坐标分别是（a，b）和（3，﹣2）；小华同学以B为原点、正东方向为x轴正半轴、正北方向为y轴正半轴、1cm长为单位长度，建立直角坐标系得到的点C恰好在二四象限的角平分线上.则a+b+8的平方根是.

查看试题解析

三、解答题：（本大题7个小题，每小题10分，共70分）解答时每小题必须给出必要的演算过程或推理步骤，画出必要的图形，请将解答过程书写在答题卡中对应的位置上。

19. 直线a，b，c，d的位置如图所示，已知∠1＝58°，∠2＝58°，∠3＝70°，求∠4的度数.

查看试题解析
20. 计算：

(1)、 $\sqrt{3}$ + $\sqrt{{(- 5)}^{2}}$ ﹣ $\sqrt[3]{64}$ ﹣| $\sqrt{3}$ ﹣5|；

(2)、（﹣2）³× $\sqrt{{(- 4)}^{2}}$ + $\sqrt[3]{{(- 4)}^{3}}$ ﹣ $\sqrt{9}$ .

查看试题解析
21. 解方程：

(1)、16（x+1）²＝49；

(2)、8（1﹣x）³＝125.

查看试题解析
22. 请你完成下面的证明：
已知：如图，∠GFB+∠B＝180°，∠1＝∠3，

求证：FC∥ED.

证明：∵∠GFB+∠B＝180°

∴FG∥BC（　             　）

∴∠3＝　▲　（　             　），

又∵∠1＝∠3（已知）

∴∠1＝　▲　（等量代换）

∴FC∥ED（　             　）

查看试题解析
23. 在平面直角坐标系中，△ABC三个顶点的位置如图（每个小正方形的边长均为1）．

(1)、请画出△ABC沿x轴向右平移3个单位长度，再沿y轴向上平移2个单位长度后的△A′B′C′（其中A′、B′、C′分别是A、B、C的对应点，不写画法）．

(2)、直接写出A′、B′、C′三点的坐标：
A′（，）； B′（，）；
C′（，）．

(3)、求△ABC的面积．

查看试题解析
24. 一个正整数，由N个数字组成，若它的第一位数可以被1整除，它的前两位数可以被2整除，前三位数可以被3整除，…，一直到前N位数可以被N整除，则这样的数叫做“精巧数”.如：123的第一位数“1”可以被1整除，前两位数“12”可以被2整除，“123”可以被3整除，则123是一个“精巧数”.

(1)、243“精巧数”（填是或不是）；3246“精巧数”（填是或不是）；

(2)、若四位数123k是一个“精巧数”，求k的值；

查看试题解析
25. 如图，在△ABC中，CD⊥AB，EF⊥AB，垂足分别为D、F.

(1)、若∠1＝∠2，试说明DG∥BC；

(2)、若CD平分∠ACB，∠A＝60°，求∠B的度数.

查看试题解析

四、解答题：（本大题1个小题，共8分）解答时每小题必须给出必要的演算过程或推理步骤，请将解答过程书写在答题卡中对应的位置上。

26. 在平面直角坐标系中，点A，B的坐标分别为A（a，0），B（b，0），且a，b满足|a+b﹣2|+ $\sqrt{2 a-b+ 5}$ ＝0，现同时将点A，B分别向右平移1个单位，再向上平移2个单位，分别得到点A，B的对应点为C，D.

(1)、请直接写出A、B、C、D四点的坐标并在坐标系中画出点A、B、C、D，连接AC，BD，CD.

(2)、点E在坐标轴上，且S_△_BCE＝S_四边形_ABDC ，求满足条件的点E的坐标.

(3)、点P是线段BD上的一个动点，连接PC，PO，当点P在线段BD上移动时（不与B，D重合）证明： $\frac{∠ D C P + ∠ B O P}{∠ C P O}$ 是个常数.

查看试题解析