湖北省武汉市武昌区拼搏联盟2020-2021学年七年级下学期数学期中考试试卷
试卷更新日期:2021-08-13 类型:期中考试
一、选择题(每小题3分,共30分)
-
1. 下列四个实数中,无理数是( )A、﹣1 B、 C、 D、2. 在平面直角坐标系中,点(﹣3,4)在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限3. 如图,点E在CB的延长线上,下列条件中,能判定AB∥CD的是( )
 A、∠1=∠4 B、∠2=∠3 C、∠A=∠ABE D、∠A+∠ABC=180°4. 如图,AB∥CD,∠1=105°,则∠2的度数是( )
A、∠1=∠4 B、∠2=∠3 C、∠A=∠ABE D、∠A+∠ABC=180°4. 如图,AB∥CD,∠1=105°,则∠2的度数是( ) A、105° B、85° C、75° D、65°5. 下列说法正确的是( )A、立方根等于本身的数是0 B、带根号的数都是无理数 C、 >5 D、 =﹣6. (﹣7)2的算术平方根是( )A、7 B、±7 C、﹣49 D、497. 下列图形中,线段AD的长表示点A到直线BC距离的是( )A、
A、105° B、85° C、75° D、65°5. 下列说法正确的是( )A、立方根等于本身的数是0 B、带根号的数都是无理数 C、 >5 D、 =﹣6. (﹣7)2的算术平方根是( )A、7 B、±7 C、﹣49 D、497. 下列图形中,线段AD的长表示点A到直线BC距离的是( )A、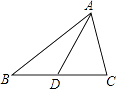 B、
B、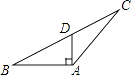 C、
C、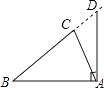 D、
D、 8. 已知点P(2m+4,m﹣1),点Q(2,5),直线PQ∥y轴,点P的坐标是( )A、(2,2) B、(16,5) C、(2,﹣2) D、(﹣2,5)9. 已知点P(x, |x|),则点P一定( )
8. 已知点P(2m+4,m﹣1),点Q(2,5),直线PQ∥y轴,点P的坐标是( )A、(2,2) B、(16,5) C、(2,﹣2) D、(﹣2,5)9. 已知点P(x, |x|),则点P一定( )
A、在第一象限 B、在第一或第四象限 C、在x轴上方 D、不在x轴下方10. 如图,CD∥AB,OE平分∠AOD,OF⊥OE,OG⊥CD,∠CDO=50°,则下列结论:①∠AOE=65°;②OF平分∠BOD;③∠GOE=∠DOF;④∠AOE=∠GOD.
其中正确结论的个数是( )
 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题(每小题3分,共18分)
-
11. = , 36的平方根是 , ﹣8的立方根是.12. 如图,已知∠1+∠2=100°,则∠3=°.
 13. 如果角α和角β的两边分别平行,且满足2α=β+60°,则角α的度数是.14. 若 ,则 (保留4个有效数字)15. 已知点A(a,0)和点B(0,5)两点,且直线AB与坐标轴围成的三角形的面积等于10,则a的值是.16. 已知字母a、b满足 ,则
13. 如果角α和角β的两边分别平行,且满足2α=β+60°,则角α的度数是.14. 若 ,则 (保留4个有效数字)15. 已知点A(a,0)和点B(0,5)两点,且直线AB与坐标轴围成的三角形的面积等于10,则a的值是.16. 已知字母a、b满足 ,则的值为.
三、解答题(共72分)
-
17. 计算:(1)、 ;(2)、 .18. 如果一个正数a的两个不同平方根是2x﹣2和6﹣3x.(1)、求这个正数a的值;(2)、求17+3a的立方根.19. 请根据条件进行推理,得出结论,并在括号内注明理由.
已知,如图,AB∥DC,直线EF分别交AB、CD于点G、H,GM、HN分别平分
∠BGH与∠DHF.

求证:GM∥HN,
证明:∵AB∥DC(已知),
∴∠BGH=∠DHF( ).
∵GM、HN分别平分∠BGH与∠DHF,
∴∠ ▲ = ∠BGH,∠ ▲ = ∠DHF(( ).
∴∠ ▲ =∠ ▲ ( ).
∴GM∥HN.( ).
20. 已知三角形ABC的边AB上任意一点P(x0 , y0)经过平移后的对应点为P1(x0+4,y0+3). (1)、将三角形ABC作同样的平移得到三角形A1B1C1 , 在下图中画出三角形A1B1C1 , 并直接写出A1、B1、C1的坐标.(2)、求出三角形ABC扫过的面积.(重叠部分不重复计算)21. 如图,直线MD、CN相交于点O,OA是∠MOC内的一条射线,OB是∠NOD内的一条射线,∠MON=70°.
(1)、将三角形ABC作同样的平移得到三角形A1B1C1 , 在下图中画出三角形A1B1C1 , 并直接写出A1、B1、C1的坐标.(2)、求出三角形ABC扫过的面积.(重叠部分不重复计算)21. 如图,直线MD、CN相交于点O,OA是∠MOC内的一条射线,OB是∠NOD内的一条射线,∠MON=70°. (1)、若∠BOD= ∠COD,求∠BON的度数;(2)、若∠AOD=2∠BOD,∠BOC=3∠AOC,求∠BON的度数.22. 如图,用两个边长为5cm的小正方形拼成一个大的正方形.
(1)、若∠BOD= ∠COD,求∠BON的度数;(2)、若∠AOD=2∠BOD,∠BOC=3∠AOC,求∠BON的度数.22. 如图,用两个边长为5cm的小正方形拼成一个大的正方形. (1)、求大正方形的边长;(2)、若沿此大正方形边长的方向剪出一个长方形,能否使剪出的长方形纸片的长宽之比为4:3,且面积为48cm2?23.
(1)、求大正方形的边长;(2)、若沿此大正方形边长的方向剪出一个长方形,能否使剪出的长方形纸片的长宽之比为4:3,且面积为48cm2?23. (1)、如图1,∠1=∠3,∠E=∠2,求证:CD∥AB.(2)、如图2,已知CD∥AB,∠MFN=120°,直线HI交∠CMF、∠FNB的角平分线分别于点H、I,求∠H﹣∠I的值.(3)、如图3,已知CD∥AB,∠MFN=α°,∠4= ∠CMF,∠5= ∠BNF,直接写出∠H﹣∠I的值为(用α表示).24. 在平面直角坐标系中(单位长度为1cm),已知点A(0,m),N(n,0),且 +|m+n﹣10|=0.
(1)、如图1,∠1=∠3,∠E=∠2,求证:CD∥AB.(2)、如图2,已知CD∥AB,∠MFN=120°,直线HI交∠CMF、∠FNB的角平分线分别于点H、I,求∠H﹣∠I的值.(3)、如图3,已知CD∥AB,∠MFN=α°,∠4= ∠CMF,∠5= ∠BNF,直接写出∠H﹣∠I的值为(用α表示).24. 在平面直角坐标系中(单位长度为1cm),已知点A(0,m),N(n,0),且 +|m+n﹣10|=0.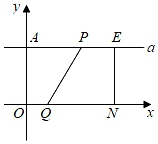 (1)、m= ,n= .(2)、如图,若点E是第一象限内的一点,且EN⊥x轴,过点E作x轴的平行线a,与y轴交于点A,点P从点E处出发,以每秒2cm的速度沿直线a向左移动,点Q从原点O同时出发,以每秒1cm的速度沿x轴向右移动.
(1)、m= ,n= .(2)、如图,若点E是第一象限内的一点,且EN⊥x轴,过点E作x轴的平行线a,与y轴交于点A,点P从点E处出发,以每秒2cm的速度沿直线a向左移动,点Q从原点O同时出发,以每秒1cm的速度沿x轴向右移动.①经过几秒PQ∥y轴?
②若某一时刻以A、O、Q、P为顶点的四边形的面积是10cm2 , 求此时点P的坐标.