湖北省武汉市黄陂区2020-2021学年七年级下学期数学期中考试试卷
试卷更新日期:2021-08-13 类型:期中考试
一、选择题(每小题3分,共30分)本题共10小题,每小题均给出A,B,C,D四个选项,有且只有一个答案是正确的,请将正确答案的代号填在答题卡上,填在试题卷上无效.
-
1. 在下面四个图形中, 与 是对顶角的是( ).A、
 B、
B、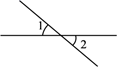 C、
C、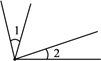 D、
D、 2. 下列各式中无意义的是( )A、 B、 C、 D、﹣3. 在平面直角坐标系中有四个点A(2,3),B(﹣2,3),C(﹣2,﹣3),D(2,﹣3),其中在第一象限的点是( )A、A B、B C、C D、D4. 如图,平行线AB,CD被直线AE所截.若∠1=105°,则∠2的度数为( )
2. 下列各式中无意义的是( )A、 B、 C、 D、﹣3. 在平面直角坐标系中有四个点A(2,3),B(﹣2,3),C(﹣2,﹣3),D(2,﹣3),其中在第一象限的点是( )A、A B、B C、C D、D4. 如图,平行线AB,CD被直线AE所截.若∠1=105°,则∠2的度数为( ) A、75° B、85° C、95° D、105°5. 下列命题中,真命题是( )A、±4是64的立方根 B、两直线被第三条直线所截,同旁内角互补 C、过直线外一点,有且只有一条直线与已知直线平行 D、如果∠1+∠2=180°,则∠1与∠2互为邻补角6. 如图,把两个面积为1dm2的小正方形分别沿对角线剪开,将所得的4个直角三角形拼接在一起,就得到一个面积为2dm2的大正方形,这个大正方形的边长是( )
A、75° B、85° C、95° D、105°5. 下列命题中,真命题是( )A、±4是64的立方根 B、两直线被第三条直线所截,同旁内角互补 C、过直线外一点,有且只有一条直线与已知直线平行 D、如果∠1+∠2=180°,则∠1与∠2互为邻补角6. 如图,把两个面积为1dm2的小正方形分别沿对角线剪开,将所得的4个直角三角形拼接在一起,就得到一个面积为2dm2的大正方形,这个大正方形的边长是( ) A、1 B、1.5 C、 D、7. 观察表格中的数据:
A、1 B、1.5 C、 D、7. 观察表格中的数据:x
16
16.1
16.2
16.3
16.4
16.5
16.6
16.7
16.8
16.9
17
y
256
259.21
262.44
265.69
268.96
272.25
275.56
278.89
282.24
285.61
289
由表格中的数据可知 在哪两个数之间( )
A、在16.2和16.3之间 B、在16.3和16.4之间 C、在16.4和16.5之间 D、在16.6和16.7之间8. 如图,AD∥BC∥x轴,下列说法正确的是( ) A、A与D的横坐标相同 B、C与D的横坐标相同 C、B与C的纵坐标相同 D、B与D的纵坐标相同9. 如图,在三角形ABC中,∠ACB=90°,过点A作AD⊥CD于点D,若AB= ,CD= ,则AC的长可能是( )
A、A与D的横坐标相同 B、C与D的横坐标相同 C、B与C的纵坐标相同 D、B与D的纵坐标相同9. 如图,在三角形ABC中,∠ACB=90°,过点A作AD⊥CD于点D,若AB= ,CD= ,则AC的长可能是( ) A、3 B、2.5 C、2 D、1.510. 如图,已知AB∥CD,M为平行线之间一点,连接AM,CM,N为AB上方一点,连接AN,CN,E为NA延长线上一点,若AM,CM分别平分∠BAE,∠DCN,则∠M与∠N的数量关系为( )
A、3 B、2.5 C、2 D、1.510. 如图,已知AB∥CD,M为平行线之间一点,连接AM,CM,N为AB上方一点,连接AN,CN,E为NA延长线上一点,若AM,CM分别平分∠BAE,∠DCN,则∠M与∠N的数量关系为( ) A、∠M﹣∠N=90° B、2∠M﹣∠N=180° C、∠M+∠N=180° D、∠M+2∠N=180°
A、∠M﹣∠N=90° B、2∠M﹣∠N=180° C、∠M+∠N=180° D、∠M+2∠N=180°二、填空题(每小题3分,共18分)下列各题不需要写出解答过程,请将结果直接填写在答题卡指定的位置.
-
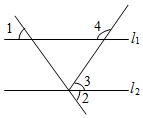
11. 的算术平方根是12. 已知点P的坐标为(2,﹣5),则P点到x轴的距离为个单位长度.13. 已知:如图,∠1=∠2=∠3=54°,则∠4的度数是 .
 14. 在平面直角坐标系中,点A的坐标为(﹣3,2).若线段AB∥x轴,且AB的长为4,则点B的坐标为.15. 如图是一个数据转换器,当输入的数x为4时,输出的y的值为;若输入有效的x后,始终输不出y的值,则满足条件的x的值为.
14. 在平面直角坐标系中,点A的坐标为(﹣3,2).若线段AB∥x轴,且AB的长为4,则点B的坐标为.15. 如图是一个数据转换器,当输入的数x为4时,输出的y的值为;若输入有效的x后,始终输不出y的值,则满足条件的x的值为. 16. 平面直角坐标系中,点A(﹣5,3),B(0,3),C(﹣5,0),在y轴左侧一点P(a,b)(b≠0且点P不在直线AB上).若∠APO=40°,∠BAP与∠COP的角平分线所在直线交于D点,则∠ADO的度数为°.
16. 平面直角坐标系中,点A(﹣5,3),B(0,3),C(﹣5,0),在y轴左侧一点P(a,b)(b≠0且点P不在直线AB上).若∠APO=40°,∠BAP与∠COP的角平分线所在直线交于D点,则∠ADO的度数为°.三、解答题(共8小题,满分72分)下列各题需要在答题卡指定的位置写出文字说明、证明过程、演算步骤或画出图形。
-
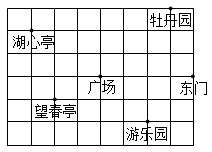
17. 计算:(1)、(2)、 .18. 春天到了,某班同学组织到公园春游,如图是公园的平面图(小正方形的边长代表100m长),图中牡丹园的坐标是(300,300),望春亭的坐标为(﹣200,﹣100),请在图中建立平面直角坐标系并写出其它地点的坐标.
 19. 在下列解题过程的空白处填上适当的内容(推理的理由或数学表达式)如图,在三角形ABC中,已知∠ADE=∠B.∠1=∠2,FG⊥AB于点G,求证:CD⊥AB.
19. 在下列解题过程的空白处填上适当的内容(推理的理由或数学表达式)如图,在三角形ABC中,已知∠ADE=∠B.∠1=∠2,FG⊥AB于点G,求证:CD⊥AB.
证明:∵∠ADE=∠B(已知),
∴DE∥ ▲ ( ),
∴∠1= ▲ ( ),
又∵∠1=∠2(已知),
∴ ▲ = ▲ (等量代换),
∴CD∥ ▲ ( ).
∵FG⊥AB(已知),
∴∠FGB=90°(垂直的定义),
即∠CDB=∠FGB=90°,
∴CD⊥AB(垂直的定义).
20. 如图,将三角形ABC向右平移2个单位长度,再向上平移3个单位长度得到三角形DEF,其中点A(﹣3,0)与点D,点B(﹣1,﹣2)与点E,点C(0,1)与点F分别对应,请解答下列问题:
( 1 )直接写出点D,E,F的坐标;
( 2 )画出△DEF,并直接写出△DEF的面积为 ▲ .
( 3 )将线段BC沿某个方向平移得到线段MN,点B的对应点为M(m,0),则点C的对应点N的坐标为 ▲ (用含m的式子表示).
21. 如图,在三角形ABC中,D是AB上一点,E是AC上一点,∠B=60°,∠BDE=120°,∠AED=45°. (1)、求证:DE∥BC;(2)、若DF平分∠ADE,交AC于点F,∠ECD=2∠BCD,求∠CDF的度数.22. 阅读下面文字,然后回答问题.
(1)、求证:DE∥BC;(2)、若DF平分∠ADE,交AC于点F,∠ECD=2∠BCD,求∠CDF的度数.22. 阅读下面文字,然后回答问题.给出定义:一个实数的整数部分是不大于这个数的最大整数,这个实数的小数部分为这个数与它的整数部分的差的绝对值.例如:2.4的整数部分为2,小数部分为2.4﹣2=0.4; 的整数部分为1,小数部分可用 ﹣1表示;再如,﹣2.6的整数部分为﹣3,小数部分为|﹣2.6﹣(﹣3)|=0.4.由此我们得到一个真命题:如果 =x+y,其中x是整数,且0<y<1,那么x=1,y= ﹣1.
(1)、如果 =a+b,其中a是整数,且0<b<1,那么a= , b=;(2)、如果﹣ =c+d,其中c是整数,且0<d<1,那么c= , d=;(3)、已知3+ =m+n,其中m是整数,且0<n<1,求|m﹣n|的值;(4)、在上述条件下,求ma+a(b+d)的立方根.23. 如图,射线PE分别与直线AB,CD相交于E,F两点,∠PFD的平分线与直线AB相交于点M,射线PM交CD于点N,设∠PFM=n∠EMF. (1)、如图1,当n=1时.
(1)、如图1,当n=1时.①试证明AB∥CD;
②点G为射线MA(不与M重合)上一点,H为射线MF(不与M,F重合)上一点,且∠MGH=∠PNF,试找出∠FMN与∠GHF之间存在的数量关系,并证明你的结论;
(2)、如图2,∠PEM=∠PME,∠PFM+∠PNF=70°.若∠EMF=20°时,直接写出n的值为.24. 在平面直角坐标系中,点A(m,n)满足n= . (1)、直接写出点A的坐标;(2)、如图1,将线段OA沿y轴向下平移a个单位后得到线段BC(点O与点B对应),过点C作CD⊥y轴于点D,若4OD=3BD,求a的值;(3)、如图2,点E(0,5)在y轴上,连接AE,将线段OA沿y轴向上平移3个单位后得到线段FG(点O与点F对应),FG交AE于点P,y轴上是否存在点Q,使S△APQ=6,若存在,请求Q点的坐标;若不存在,请说明理由.
(1)、直接写出点A的坐标;(2)、如图1,将线段OA沿y轴向下平移a个单位后得到线段BC(点O与点B对应),过点C作CD⊥y轴于点D,若4OD=3BD,求a的值;(3)、如图2,点E(0,5)在y轴上,连接AE,将线段OA沿y轴向上平移3个单位后得到线段FG(点O与点F对应),FG交AE于点P,y轴上是否存在点Q,使S△APQ=6,若存在,请求Q点的坐标;若不存在,请说明理由.