湖北省武汉市洪山区2020-2021学年七年级下学期数学期中考试试卷
试卷更新日期：2021-08-13 类型：期中考试
一、选择题
-
1. 下列图案是由图中所示的图案通过平移后得到的是（ ）
A、
B、
C、
D、
2. 如图，D，E，F分别在△ABC的三边上，能判定DE∥AC的条件是（ ）
A、∠1+∠2＝180° B、∠1＝∠3 C、∠2＝∠4 D、∠3＝∠C3. 已知点Q的坐标为（﹣2+a，2a﹣7），且点Q到两坐标轴的距离相等，则点Q的坐标是（ ）A、（3，3） B、（3，﹣3） C、（1，﹣1） D、（3，3）或（1，﹣1）4. 下列说法中正确的个数为（ ）①在平面内，两条直线的位置关系只有两种：相交和垂直；
②在平面内，过一点有且只有一条直线与已知直线垂直；
③在平面内，过一点有且只有一条直线与已知直线平行；
④如果两条直线都与第三条直线平行，那么这两条直线也互相平行；
⑤从直线外一点到这条直线的垂线段，叫做这个点到这条直线的距离.
A、2个 B、3个 C、4个 D、5个5. 如图，已知长方形纸片ABCD，点E，F在AD边上，点G，H在BC边上，分别沿EG，FH折叠，使点D和点A都落在点M处，若α+β＝119°，则∠EMF的度数为（ ）
A、57° B、58° C、59° D、60°6. 如图，已知直线AB，CD被直线AC所截，AB∥CD，E是平面内CD上方的一点（点E不在直线AB，CD，AC上），设∠BAE＝α，∠DCE＝β.下列各式：①α+β，②α﹣β，③β﹣α，④180°﹣α﹣β，⑤360°﹣α﹣β中，∠AEC的度数可能是（ ）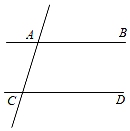
A、①②③ B、①②④⑤ C、①②③⑤ D、①②③④⑤二、填空题
-
7. 若a3＝8， ＝2，则a+b＝.8. 如图，若在象棋棋盘上建立平面直角坐标系，使“兵”位于点（1，﹣1），“炮”位于点（﹣1，0），则“马”位于点.
9. 定义：f（x，y）＝（﹣x，﹣y），g（a，b）＝（b，a），例如：f（1，2）＝（﹣1，﹣2），g（2，3）＝（3，2），则g（f（﹣5，2））＝.三、解答题
-
10. 如图，BD平分∠ABC，F在AB上，G在AC上，FC与BD相交于点H，∠3+∠4＝180°，试说明∠1＝∠2.（请通过填空完善下列推理过程）
解：∵∠3+∠4＝180°（已知），∠FHD＝∠4（ ）.
∴∠3+ ▲ ＝180°（等量代换）.
∴FG∥BD（ ）.
∴∠1＝ ▲ （ ）.
∵BD平分∠ABC，
∴∠ABD＝ ▲ （ ）.
∴∠1＝∠2（ ）.
11. 如图，D，E分别在△ABC的边AB，AC上，F在线段CD上，且∠1+∠2＝180，DE∥BC.
(1)、求证：∠3＝∠B；(2)、若DE平分∠ADC，∠2＝3∠B，求∠1的度数.12. 【学科融合】物理学中把经过入射点O并垂直于反射面的直线ON叫做法线，入射光线与法线的夹角i叫做入射角，反射光线与法线的夹角r叫做反射角（如图①）.由此可以归纳出如下的规律：
在反射现象中，反射光线、入射光线和法线都在同一平面内；反射光线、入射光线分别位于法线两侧；反射角等于入射角.这就是光的反射定律（rfectionlaw）.
【数学推理】如图1，有两块平面镜OM，ON，且OM⊥ON，入射光线AB经过两次反射，得到反射光线CD.由以上光的反射定律，可知入射角与反射角相等，进而可以推得他们的余角也相等，即：∠1＝∠2，∠3＝∠4.在这样的条件下，求证：AB∥CD.
【尝试探究】两块平面镜OM，ON，且∠MON＝α，入射光线AB经过两次反射，得到反射光线CD.
(1)、如图2，光线AB与CD相交于点E，则∠BEC＝；(2)、如图3，光线AB与CD所在的直线相交于点E，CBED＝β，则α与β之间满足的等量关系是.