重庆市江北区2020-2021学年九年级下学期数学期中考试试

试卷更新日期：2021-08-13 类型：期中考试

进入出卷网下载

一、选择题：（本大题12个小题，每小题4分，共48分）在每个小题的下面，都给出了代号为A、B、C、D的四个答案，其中只有一个是正确的，请将答题卡上题号右侧正确答案所对应的方框涂黑。

1. 我国是最早使用负数的国家，东汉初，在我国著名的数学书《九章算术》中，明确提出了“正负术”.如果盈利20元记作“+20元”，那么亏损30元记作（　　）

A、﹣30元 B、30元 C、50元 D、﹣50元

查看试题解析
2. 如图两个长方体如图放置，则该立方体图形的左视图是（　　）

A、 B、 C、 D、

查看试题解析
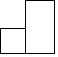3. 计算a•a结果正确的是（　　）

A、a B、a² C、a³ D、a⁴

查看试题解析
4. 如图，⊙O中，CD是切线，切点是D，直线CO交⊙O于B，A，∠A＝15°，则∠C的度数是（　　）

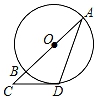A、45° B、65° C、60° D、70°

查看试题解析
5. 下列各式中，与 $\sqrt{2}$ 的积为有理数的是（　　）

A、 $\sqrt{8}$ B、 $\sqrt{12}$ C、 $\sqrt{24}$ D、 $\sqrt{27}$

查看试题解析
6. 如图，△ABC与△DEF位似，点O为位似中心.已知OA：OD＝1：2，则△ABC与△DEF的面积比为（）

A、1：2 B、1：3 C、1：4 D、1：5

查看试题解析
7. 某种商品的进价为500元，出售时标价为750元，由于换季，商店准备打折销售，但要保持利润不低于20%，那么至多打（　　）

A、6折 B、7折 C、8折 D、9折

查看试题解析
8. 根据如图所示的程序计算函数y的值，若输入的x值是﹣3和4时，输出的y值相等，则m等于（　　）

A、﹣17 B、﹣25 C、25 D、﹣43

查看试题解析
9. 春节期间，某老师读到《行路难》中“闲来垂钓碧溪上，忽复乘舟梦日边.”邀约好友一起在江边垂钓，如图，河堤AB的坡度为1：2.4，AB长为5.2米，钓竿AC与水平线的夹角是60°，其长为6米，若钓竿AC与钓鱼线CD的夹角也是60°，则浮漂D与河堤下端B之间的距离约为（　　）（参考数据： $\sqrt{3}$ ＝1.732）

A、2.33米 B、2.35米 C、2.36米 D、2.42米

查看试题解析
10. 从﹣4，﹣3，1，3，4这五个数中，随机抽取一个数，记为m，若m使得关于x，y的二元一次方程组 ${\begin{cases} 2 x + y = 2 \\ m x - 2 y = - 3 \end{cases}$ 有解，且使关于x的分式方程 $\frac{1 - m}{x - 1}$ ﹣1＝ $\frac{2}{1 - x}$ 有正数解，那么这五个数中所有满足条件的m的值之和是（　　）

A、1 B、2 C、﹣1 D、﹣2

查看试题解析
11. 如图，在Rt△ABC中，∠C＝90°，AC＝6，BC＝9，点D为BC边上的中点，将△ACD沿AD对折，使点C落在同一平面内的点C′处，连接BC′，则BC′的长为（　　）

A、 $\frac{9}{2}$ B、 $\frac{27}{5}$ C、3 $\sqrt{2}$ D、2 $\sqrt{3}$

查看试题解析
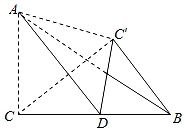12. 如图，Rt△ADC在平面直角坐标系下如图放置，斜边AC交x轴于点E，过点A的双曲线y＝ $\frac{k}{x}$ （k≠0）过Rt△ADC斜边AC的中点B，连接BD，过点C作双曲线y＝ $\frac{m}{x}$ （m≠0）.若BD＝3BE，A的坐标为（1，6），则m＝（　　）

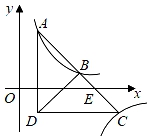A、﹣15 B、﹣21 C、﹣28 D、﹣36

查看试题解析

二、填空题：（本大题6个小题，每小题4分，共24分）请将每小题的答案直接填在答题卡中对应的横线上。

13. （π﹣4）⁰+（﹣ $\frac{1}{3}$ ）^﹣¹＝.

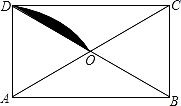
查看试题解析
14. 引发春季传染病的某种病毒的直径是0.000000025，将0.000000025用科学记数法表示为.

查看试题解析
15. 现将背面完全相同，正面分别标有数0，1，3，5的4张卡片洗匀后，背面朝上，从中任取一张，将该卡片上的数标记为m，再从剩下的3张卡片中任取一张，将该卡片上的数记为n，则数字m，n都为奇数的概率为.

查看试题解析
16. 如图，矩形ABCD的对角线AC、BD相交于点O，AO＝AD＝2，以A为圆心，AO为半径作弧，则图中阴影部分的面积为.

查看试题解析
17. 周末，步行爱好者甲、乙两人沿同一路线分别从A、B两地相向而行，匀速行进，甲先出发且先到达B地，甲、乙两人相距的路程y（单位：km）与甲出发的时间x（单位：h）之间的关系如图所示，则甲到达B地时，乙距离A地km.

查看试题解析
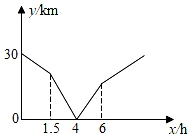18. 某中学科技节颁奖仪式隆重举行，其中小科技创新发明奖共有60人获奖，原计划特等奖5人，一等奖15人，二等奖40人.后来经校领导开会研究决定，在该项奖励总奖金不变的情况下，各等级获奖人数实际调整为：特等奖8人，一等奖18人，二等奖34人，调整后特等奖每人奖金降低90元，一等奖每人奖金降低50元，二等奖每人奖金降低30元，调整前一等奖每人奖金比二等奖每人奖金多70元，则调整后特等奖每人奖金比一等奖每人奖金多元.

查看试题解析

三、解答题：（本大题7个小题，每小题10分，共70分）解答时每小题必须给出必要的演算过程或推理步骤，画出必要的图形（包括辅助线），请将解答过程写在答题卡中对应的位置上。

19. 化简下列各式：

(1)、（a﹣2b）²+（a﹣b）（a+4b）；

(2)、 $\frac{x^{2} - 9}{x + 2} \div (\frac{6 x + 13}{x + 2} + x - 2)$ .

查看试题解析
20. 如图，在平行四边形ABCD中，AE，CF分别平分∠BAD和∠DCB，交对角线BD于点E，F.

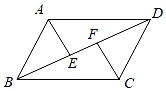(1)、若∠BCF＝55°，求∠ABC的度数；

(2)、求证：BE＝DF.

查看试题解析

21. 为了迎接即将到来的“学业水平暨高中招生考试”，同学们通过模拟考试来调整自己的状态并了解自己的学业水平.某中学物理教研组想通过此次中考模拟的成绩来预估中考的各个分数段人数，在全年级随机抽取了男、女各40名学生的成绩（满分为80分，女生成绩中最低分为45分），并将数据进行整理分析，给出了部分信息：

①男生成绩扇形统计图和女生成绩频数分布直方图：

（数据分组为A组：x＜50；B组：50≤x＜60；C组：60≤x＜70；D组：70≤x＜80）

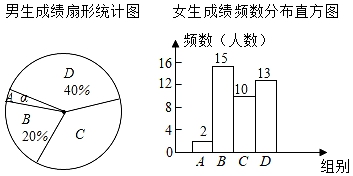
②男生C组中全部14名学生的成绩为：

61，62，63，64，65，66，66，66，67，68，69，69，69，69.

③两组数据的平均数、中位数、众数、满分率（单位：分）如下表所示：

	平均数	中位数	众数	满分率
男生	70	b	c	25%
女生	70	67	78	15%

(1)、扇形统计图A组学生中所对应的圆心角α的度数为，中位数b＝，众数c＝；

(2)、通过以上的数据分析，你认为（填“男生”或“女生”）的物理成绩更好，并说明理由：；

(3)、若成绩在70分（包含70分）以上为优秀，请你估计该校1200名学生在此次考试中优秀的人数.

查看试题解析

22. 定义：一个四位数的自然数，记千位上和十位上的数字之和为x，百位上和个位上的数字之和为y，如果x＝y，那么称这个四位数为“协调数”.
例如：3245，x＝3+4，y＝2+5，因为x＝y，所以3245是“协调数”.

(1)、直接写出：最小的“协调数”是，最大的“协调数”是；

(2)、求个位上的数字是千位上的数字的两倍且百位上的数字与十位上的数字之和是7的倍数的所有“协调数”.

查看试题解析

23. 在初中阶段的函数学习中，我们经历了列表、描点、连线画函数图象，并结合图象研究函数性质的过程，以下是我们研究函数y＝

\frac{y_{1}}{y_{2}}

（其中y₂与x成反比例，y₁＝x²+6x）性质及其应用的部分过程，请按要求完成下列各小题.

(1)、请写出解析式为　▲　；并把下表补充完整，且在图中补全该函数图象；

x	…	﹣6	﹣5	﹣4	﹣3	﹣2	﹣1	0	1	…
y	…	0	$\frac{25}{8}$		$\frac{27}{8}$		$\frac{5}{8}$	0	$\frac{7}{8}$	…

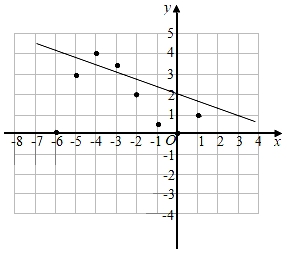(2)、根据函数图象，判断下列关于该函数性质的说法是否正确，正确的在答题卡上相应的括号内打“√”，错误的在答题卡上相应的括号内打“×”；

①该函数在自变量的取值范围内，有最大值和最小值.当x＝﹣4时，函数取得最大值4；当x＝0时，函数取得最小值0.（）

②当x＜﹣4时，y随x的增大而增大；当﹣4≤x≤0时，y随x的增大而减小；当x＞0时，y随x的增大而增大.（）

(3)、已知函数y＝﹣

\frac{1}{3}

x+2的图象如图所示，结合你所画的函数图象，直接写出方程

\frac{1}{8}

x³+

\frac{3}{4}

x²+

\frac{1}{3}

x＝2的近似解（保留1位小数，误差不超过0.2）.

查看试题解析

24. 按照中央精准扶贫的部署，市委、市政府重点扶持贫困户发展特色农业.现某区扶持一贫困户的李子园销售“金脆李”和“黄橙李”两种李子，因为“金脆李”果形奇特、口感佳，售价为30元/斤，“黄橙李”因大面积种植，售价要便宜一些，为20元/斤.

(1)、7月上旬，该果园一共售出300斤李子，要使销售额不低于7250元，问最多售出“黄橙李”多少斤？

(2)、为了提高“金脆李”的知名度，政府对“金脆李”进行广告宣传，7月中旬该果园的总销售重量为1500斤，其中售出“黄橙李”1000斤，7月下旬由于李子大量上市，该果园推出优惠方案，“金脆李”每斤降价a%，“黄橙李”售价保持不变，售后统计“金脆李”销售数量在7月中旬的基础上增加了2a%，“黄橙李”数量在7月中旬的基础上减少了 $\frac{3}{16}$ a%，若总销售额与7月中旬的总销售额持平，求a的值.

查看试题解析
25. 如图，抛物线y＝ $- \frac{\sqrt{3}}{6} x^{2} + \frac{2 \sqrt{3}}{3} x + 2 \sqrt{3}$ 与x轴交于A，B两点（点A在点B右侧），与y轴交于点C，点D是抛物线的顶点.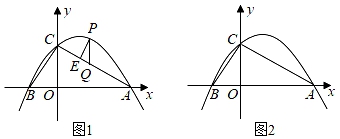

(1)、如图1，连接AC，BC，判断△ABC的形状，说明理由；

(2)、如图2，若点P是直线AC上方抛物线上一动点，过点P作PE∥BC交AC于点E，作PQ∥y轴交AC于点Q，求CE+AQ的最小值及此时E点坐标；

(3)、将该抛物线向左平移2个单位长度得到抛物线y＝a₁x²+b₁x+c₁（a₁≠0），平移后的抛物线与原抛物线相交于点P，点Q为原抛物线对称轴上的一点，在平面直角坐标系中是否存在点M，使以点A，P，Q，M为顶点的四边形为菱形，若存在，请直接写出点M的坐标；若不存在，请说明理由.

查看试题解析

四、解答题：（本大题1个小题，共8分）解答时必须给出必要的演算过程或推理步骤，画出必要的图形（包括辅助线），请将解答过程书写在答题卡中对应的位置上。

26. 已知△ABC为等边三角形，点D为直线BC上一动点（点D不与B，C重合）.在AD右侧，以AD为边作菱形ADEF，使∠DAF＝60°，连接CF.

(1)、如图1，当点D在边BC上时，请写出∠AFC，∠DAC，∠ABC之间存在的数量关系；

(2)、如图2，当点D在边BC的延长线上时，其他条件不变，请写出∠AFC，∠DAC，∠ABC之间存在的数量关系，并写出证明过程；

(3)、如图3，当点D在边CB的延长线上时，且点A，F分别在直线BC的异侧，其他条件不变，请补全图形，并直接写出∠AFC，∠DAC，∠ABC之间存在的等量关系.

查看试题解析