甘肃省张掖市甘州区2020-2021年九年级下学期数学期中考试试卷

试卷更新日期：2021-08-13 类型：期中考试

进入出卷网下载

一、选择题（30分）

1. 4的平方根是（　　）

A、2 B、﹣2 C、± $\sqrt{2}$ D、±2

查看试题解析
2. 下列运算正确的是（　　）

A、a²•a³＝a⁵ B、（﹣a）⁴＝﹣a⁴ C、（a²）³＝a⁵ D、a²+a⁴＝a⁶

查看试题解析
3. 下面四个图形分别是节能、节水、低碳和绿色食品标志，是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
4. 如图，直线a，b被直线c所截，a∥b，∠2＝∠3，若∠1＝80°，则∠4等于（　　）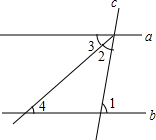

A、20° B、40° C、60° D、80°

查看试题解析
5. 如图，若在象棋盘上建立直角坐标系，使“帅”位于点（﹣1，﹣2）.“馬”位于点（2，﹣2），则“兵”位于点（　　）

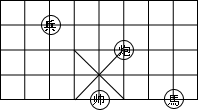A、（﹣1，1） B、（﹣2，﹣1） C、（﹣3，1） D、（1，﹣2）

查看试题解析
6. 某社区青年志愿者小分队年龄情况如下表所示：

年龄（岁）

18

19

20

21

22

人数

2

5

2

2

1

则这12名队员年龄的众数、中位数分别是（　　）

A、2岁，20岁 B、2岁，19岁 C、19岁，20岁 D、19岁，19岁

查看试题解析
7. 如图，AB是⊙O的直径，AB＝4，AC是弦，AC＝2 $\sqr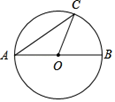t{3}$ ，∠AOC＝（　　）

A、120° B、130° C、140° D、150°

查看试题解析
8. 二次函数y＝﹣x²+2x+2化为y＝a（x﹣h）²+k的形式，下列正确的是（　　）

A、y＝﹣（x﹣1）²+2 B、y＝﹣（x﹣1）²+3 C、y＝（x﹣2）²+2 D、y＝（x﹣2）²+4

查看试题解析
9. 甲、乙二人做某种机械零件，已知每小时甲比乙少做8个，甲做120个所用的时间与乙做150个所用的时间相等，设甲每小时做x个零件，下列方程正确的是（）

A、 $\frac{120}{x} = \frac{150}{x - 8}$ B、 $\frac{120}{x + 8} = \frac{150}{x}$ C、 $\frac{120}{x - 8} = \frac{150}{x}$ D、 $\frac{120}{x} = \frac{150}{x + 8}$

查看试题解析
10. 如图，每一图中有若干个大小不同的菱形，第一幅图中有1个菱形，第二幅图中有3个菱形，第三幅图中有5个菱形，如果第n幅图中有2021个菱形，则n为（　　）

A、1000 B、1010 C、1011 D、2020

查看试题解析

二、填空题（32分）

11. 分解因式：x²y²﹣9y²＝.

查看试题解析
12. 若式子 $\frac{\sqrt{x + 2}}{x}$ 有意义，则x的取值范围是．

查看试题解析
13. 已知关于x的一元二次方程kx²﹣2 $\sqrt{3}$ x+1＝0有两个不相等的实数根，则k的取值范围是.

查看试题解析
14. 已知在Rt△ABC中，∠C＝90°，sin A＝ $\frac{12}{13}$ ，则tan B的值为.

查看试题解析
15. 定义一种新的运算：x*y= $\frac{x + 2 y}{x}$ ，如：3*1= $\frac{3 + 2 \times 1}{3}$ = $\frac{5}{3}$ ，则（2*3）*2= ．

查看试题解析
16. 如图，AB是⊙O的直径，点C，D在⊙O上.若∠D＝50°，则∠BAC等于 .

查看试题解析
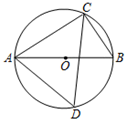17. 如图，直角三角形纸片的两直角边长分别为6，8，现将其如图那样折叠，使点A与点B重合，折痕为DE，则DE的值是.

查看试题解析
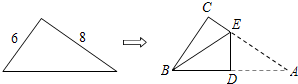18. 如图1，四边形ABCD中，AB∥CD，∠B＝90°，AC＝AD.动点P从点B出发沿折线B﹣A﹣D﹣C方向以1单位/秒的速度匀速运动，在整个运动过程中，△BCP的面积S与运动时间t（秒）的函数图象如图2所示，写出
①AB＝；②CD＝（提示：过A作CD的垂线）；③BC＝.

查看试题解析

三、解答题（88分）

19.

(1)、计算： $\sqrt{8}$ ﹣2sin45°+（2﹣π）⁰﹣（ $\frac{1}{3}$ ）^﹣¹；

(2)、解方程：x²﹣2x﹣3＝0.

查看试题解析
20. 古诗中，五言绝句是四句诗，每句都是五个字；七言绝句是四句诗，每句都是七个字，有一本诗集，五言绝句比七言绝句多13首，总字数却反而少了20个字，则这本诗集中两种诗各多少首？

查看试题解析
21. 如图，在边长为1的正方形组成的网格中，△AOB的顶点均在格点上，点A，B的坐标分别是A（3，3）、B（1，2），△AOB绕点O逆时针旋转90°后得到△A₁OB₁.

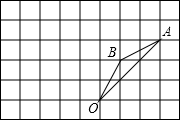(1)、画出△A₁OB₁ ，直接写出点A₁ ， B₁的坐标；

(2)、在旋转过程中，点B经过的路径的长；

(3)、求在旋转过程中，线段AB所扫过的面积.

查看试题解析
22. 国庆70周年，某校举行班级“唱红歌”歌咏比赛，歌曲有：A：《没有共产党就没有新中国》，B：《我和我的祖国》；C：《走进新时代》.比赛时，将A、B、C这三个字母分别写在3张无差别不透明的卡片正面上，洗匀后正面向下放在桌面上，1班班长先从中随机抽取一张卡片，放回后洗匀.再由2班班长从中随机拍取一张卡片，进行歌咏比赛.

(1)、1班抽中歌曲《我和我的祖国）的概率是.

(2)、试用画树状图或列表的方法求出1班和2班抽中不同歌曲的概率.

查看试题解析
23. 图1是安装在倾斜屋顶上的热水器，图2是安装热水器的侧面示意图.已知屋面AE的倾斜角∠EAD为22°，长为2米的真空管AB与水平线AD的夹角为37°，安装热水器的铁架竖直管CE的长度为0.5米.

(1)、真空管上端B到水平线AD的距离.

(2)、求安装热水器的铁架水平横管BC的长度(结果精确到0.1米)
参考数据：sin37°≈ $\frac{3}{5}$ ，cos37°≈ $\frac{4}{5}$ ，tan37°≈ $\frac{3}{4}$ ，sin22°≈ $\frac{3}{8}$ ，cos22°≈ $\frac{15}{16}$ ，tan22°≈ $\frac{2}{5}$

查看试题解析

24. 某校有3000名学生.为了解全校学生的上学方式，该校数学兴趣小组以问卷调查的形式，随机调查了该校部分学生的主要上学方式（参与问卷调查的学生只能从以下六个种类中选择一类）：

种类	A	B	C	D	E	F
上学方式	电动车	私家车	公共交通	自行车	步行	其他

并将调查结果绘制成如下不完整的统计图：

根据以上信息，回答下列问题：

(1)、参与本次问卷调查的学生共有人，其中选择B类的人数有人.

(2)、在扇形统计图中，求E类对应的扇形圆心角α的度数，并补全条形统计图中C对应的直条.

(3)、若将A，C，D，E这四类上学方式视为“绿色出行”，请估计该校每天“绿色出行”的学生人数.

查看试题解析

25. 如图，在平面直角坐标系中，四边形ABCD为正方形，点A的坐标为（0，3），点B的坐标为（0，﹣4），反比例﹣函数y＝ $\frac{k}{x}$ （k≠0）的图象经过点C.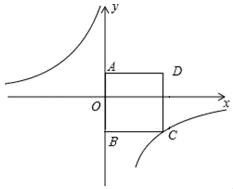

(1)、求反比例函数的解析式；

(2)、点P是反比例函数在第二象限的图象上的一点，若△PBC的面积等于正方形ABCD的面积，求点P的坐标.

查看试题解析
26. 如图，已知△ABC中，AB＝AC，以AB为直径的⊙O交CB于D，E为AB延长上一点，∠C+∠BDE＝90°.

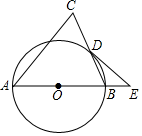(1)、求证：DE是⊙O的切线.

(2)、若BE＝2，tan∠ABC＝ $\sqrt{5}$ ，求⊙O的半径.

查看试题解析
27. 【方法提炼】
解答几何问题常常需要添辅助线，其中平移图形是重要的添辅助线策略.

【问题情境】

如图1，在正方形ABCD中，E，F，G分别是BC，AB，CD上的点，FG⊥AE于点Q.求证：AE＝FG.

小明在分析解题思路时想到了两种平移法：

方法1：平移线段FG使点F与点B重合，构造全等三角形；

方法2：平移线段BC使点B与点F重合，构造全等三角形；

【尝试应用】

(1)、请按照小明的思路，选择其中一种方法进行证明；

(2)、如图2，正方形网格中，点A，B，C，D为格点，AB交CD于点O.求tan∠AOC的值；

(3)、如图3，点P是线段AB上的动点，分别以AP，BP为边在AB的同侧作正方形APCD与正方形PBEF，连接DE分别交线段BC，PC于点M，N.
①求∠DMC的度数；

②连接AC交DE于点H，求 $\frac{D H}{B C}$ 值.

查看试题解析
28. 如图，抛物线y＝ax²+bx+c经过点A（﹣3，0），B（1，0），C（0，﹣3）.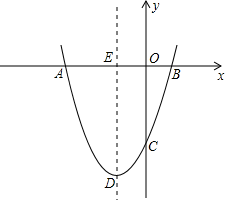

(1)、求抛物线的解析式；

(2)、若点P为第三象限内抛物线上的一点，设△PAC的面积为S，求S的最大值并求出此时点P的坐标；

(3)、设抛物线的顶点为D，DE⊥x轴于点E，在y轴上是否存在点M，使得△ADM是直角三角形？若存在，请直接写出点M的坐标；若不存在，请说明理由.

查看试题解析

年龄（岁）	18	19	20	21	22
人数	2	5	2	2	1