初中数学浙教版九年级上册3.8 弧长及扇形的面积同步练习
试卷更新日期:2021-08-12 类型:同步测试
一、单选题
-
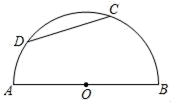
1. 某小区内的消防车道有一段弯道,如图,弯道的内外边缘均为圆弧, , 所在圆的圆心为O,点C,D分别在OA,OB上,已知消防车道半径OC=12m,消防车道宽AC=4m, ,则弯道外边缘 的长为( )
 A、 B、 C、 D、2. 已知圆心角为60°的扇形面积为 ,则扇形的弧长为( )A、4 B、2 C、 D、3. 若扇形的半径为3,圆心角为60°,则此扇形的弧长是( )A、 π B、π C、 π D、2π4. 在 Rt△ABC 中,∠B=90°,BC=15,AC=17,以 AB 为直径作半圆,则此半圆的面积( )A、 B、 C、 D、5. 中国美食讲究色香味美,优雅的摆盘造型:也会让美食锦上添花.图①中的摆盘,其形状是扇形的一部分,图②是一个摆盘的几何示意图(阴影部分为摆盘),通过测量得到AC=BD=12cm,C、D两点之间的距离为4cm,圆心角为60°,则图②的摆盘的面积是( )
A、 B、 C、 D、2. 已知圆心角为60°的扇形面积为 ,则扇形的弧长为( )A、4 B、2 C、 D、3. 若扇形的半径为3,圆心角为60°,则此扇形的弧长是( )A、 π B、π C、 π D、2π4. 在 Rt△ABC 中,∠B=90°,BC=15,AC=17,以 AB 为直径作半圆,则此半圆的面积( )A、 B、 C、 D、5. 中国美食讲究色香味美,优雅的摆盘造型:也会让美食锦上添花.图①中的摆盘,其形状是扇形的一部分,图②是一个摆盘的几何示意图(阴影部分为摆盘),通过测量得到AC=BD=12cm,C、D两点之间的距离为4cm,圆心角为60°,则图②的摆盘的面积是( ) A、80πcm2 B、40πcm2 C、24πcm2 D、2πcm26. 如图,⊙O是正五边形ABCDE的外接圆.若⊙O的半径为5,则半径OA , OB与 围成的扇形的面积是( )
A、80πcm2 B、40πcm2 C、24πcm2 D、2πcm26. 如图,⊙O是正五边形ABCDE的外接圆.若⊙O的半径为5,则半径OA , OB与 围成的扇形的面积是( )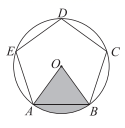 A、 B、 C、 D、7. 如图,从一张腰长为 ,顶角为 的等腰三角形铁皮 中剪出一个最大的扇形 ,用此剪下的扇形铁皮围成一个圆锥的侧面(不计损耗),则该圆锥的底面周长为( )
A、 B、 C、 D、7. 如图,从一张腰长为 ,顶角为 的等腰三角形铁皮 中剪出一个最大的扇形 ,用此剪下的扇形铁皮围成一个圆锥的侧面(不计损耗),则该圆锥的底面周长为( ) A、 B、 C、 D、8. 如图,在Rt△ABC中,∠A=90°,BC= .以BC的中点O为圆心的⊙O分别与AB , AC相切于D , E两点,则 的长为( )
A、 B、 C、 D、8. 如图,在Rt△ABC中,∠A=90°,BC= .以BC的中点O为圆心的⊙O分别与AB , AC相切于D , E两点,则 的长为( ) A、 B、π C、2π D、4π9. 如图,一块直角三角板的60°角的顶点A落在⊙O上,两边分别交⊙O于B,C两点,若⊙O的半径是1,则 的长是( )
A、 B、π C、2π D、4π9. 如图,一块直角三角板的60°角的顶点A落在⊙O上,两边分别交⊙O于B,C两点,若⊙O的半径是1,则 的长是( ) A、 B、 C、 D、10. 二十四节气,是我国古人根据地球在黄道(即地球绕太阳公转的轨道)上的位置变化而制定的,每一个节气分别相对应于地球在黄道上每运转15°所到达的一定位置,反映了太阳对地球产生的影响.它凝聚着中华文明的历史文化精华,在国际气象界,二十四节气被誉为“中国的第五大发明”.如图是地球绕太阳公转的轨道图,若将其近似看作圆形,其半径为Rkm,则从每年的立春到立夏,地球绕太阳公转的路程是( )
A、 B、 C、 D、10. 二十四节气,是我国古人根据地球在黄道(即地球绕太阳公转的轨道)上的位置变化而制定的,每一个节气分别相对应于地球在黄道上每运转15°所到达的一定位置,反映了太阳对地球产生的影响.它凝聚着中华文明的历史文化精华,在国际气象界,二十四节气被誉为“中国的第五大发明”.如图是地球绕太阳公转的轨道图,若将其近似看作圆形,其半径为Rkm,则从每年的立春到立夏,地球绕太阳公转的路程是( ) A、 km B、 km C、 km D、 km
A、 km B、 km C、 km D、 km二、填空题
-
11. 如图所示的扇形中,已知 ,则 .
 12. 如图是圆弧形状的铁轨示意图,半径OA的长度为200米,圆心角 ,则这段铁轨的长度米,(铁轨的宽度忽略不计,结果保留π)
12. 如图是圆弧形状的铁轨示意图,半径OA的长度为200米,圆心角 ,则这段铁轨的长度米,(铁轨的宽度忽略不计,结果保留π)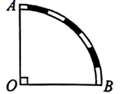 13. 如图是一个由三条等弧围成的莱洛三角形,其中 的圆心为点 , .若 ,则该三角形的周长是 .
13. 如图是一个由三条等弧围成的莱洛三角形,其中 的圆心为点 , .若 ,则该三角形的周长是 . 14. 扇形的半径为5,圆心角等于120°,则扇形的面积等于 .15. 如图,△ABC内接于半径为2的⊙O,∠ABC、∠ACB 的平分线交于点I,∠BIC=110°,则劣弧BC的长为 .
14. 扇形的半径为5,圆心角等于120°,则扇形的面积等于 .15. 如图,△ABC内接于半径为2的⊙O,∠ABC、∠ACB 的平分线交于点I,∠BIC=110°,则劣弧BC的长为 . 16. 已知扇形的半径为4cm,圆心角为150°,则扇形的弧长为cm.
16. 已知扇形的半径为4cm,圆心角为150°,则扇形的弧长为cm.三、解答题
-
17. 如图,折扇完全打开后,OA,OB的夹角为120°,OA的长为18cm,AC的长为9cm,求图中阴影部分的面积S.
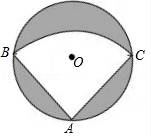
 18. 已知半径为6的扇形面积为 ,求此扇形圆心角的角度.19. 如图,⊙A、⊙B、⊙C两两不相交,且半径都是2cm,图中的三个扇形(即三个阴影部分)的面积之和是多少?弧长的和为多少?
18. 已知半径为6的扇形面积为 ,求此扇形圆心角的角度.19. 如图,⊙A、⊙B、⊙C两两不相交,且半径都是2cm,图中的三个扇形(即三个阴影部分)的面积之和是多少?弧长的和为多少? 20. 已知圆环的大圆半径R=4cm,小圆半径r=2cm,求圆环的面积。
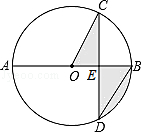
20. 已知圆环的大圆半径R=4cm,小圆半径r=2cm,求圆环的面积。 21. 如图,半圆O的直径AB=6,弦CD=3, 的长为 π,求 的长.
21. 如图,半圆O的直径AB=6,弦CD=3, 的长为 π,求 的长.