初中数学浙教版九年级上册3.7 正多边形同步练习

试卷更新日期：2021-08-12 类型：同步测试

进入出卷网下载

一、单选题

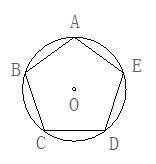
1. 在正六边形ABCDEF的中，若BE=10，则这个正六边形外接圆半径是（）

A、 $\frac{5}{2}$ B、5 C、 $\frac{5}{2} \sqrt{3}$ D、5 $\sqrt{3}$

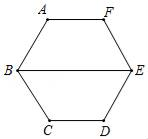查看试题解析
2. ⊙O是一个正n边形的外接圆，若⊙O的半径与这个正n多边形的边长相等，则n的值为（　　）

A、3 B、4 C、5 D、6

查看试题解析
3. 已知圆内接正六边形的半径为2，则该内接正六边形的边心距为（）

A、2 B、1 C、 $\sqrt{3}$ D、 $\frac{\sqrt{3}}{2}$

查看试题解析
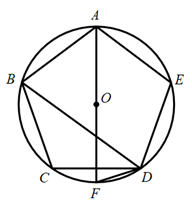4. 如图，五边形 $A B C D E$ 是 $⊙ O$ 的内接正五边形， $A F$ 是 $⊙ O$ 的直径，则 $∠ B D F$ 的度数是（）

A、18° B、36° C、 $54 °$ D、72°

查看试题解析
5. 如图，正六边形ABCDEF内接于于⊙O，连接BD，则∠CBD的度数是（）

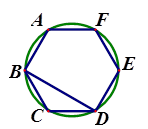A、30° B、45° C、60° D、90°

查看试题解析
6. 已知正六边形 $A B C D E F$ 内接于 $⊙ O$ ，若 $⊙ O$ 的直径为 $2$ ，则该正六边形的周长是（）

A、 $12$ B、 $6 \sqrt{3}$ C、 $6$ D、 $3 \sqrt{3}$

查看试题解析
7. 半径为 $a$ 的圆的内接正六边形的边心距是（）

A、 $\frac{a}{2}$ B、 $\frac{\sqrt{2} a}{2}$ C、 $\frac{\sqrt{3} a}{2}$ D、 $a$

查看试题解析
8. 半径为 $R$ 的圆内接正三角形的面积是（）

A、 $\frac{\sqrt{3}}{2} R^{2}$ B、 $π R^{2}$ C、 $\frac{3 \sqrt{3}}{2} R^{2}$ D、 $\frac{3 \sqrt{3}}{4} R^{2}$

查看试题解析
9. 如图，在圆内接正六边形ABCDEF中，BF，BD分别交AC于点G，H.若该圆的半径为15cm，则线段GH的长为（）

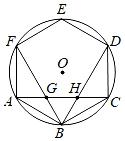A、 $\sqrt{5}$ cm B、5 $\sqrt{3}$ cm C、3 $\sqrt{5}$ cm D、10 $\sqrt{3}$ cm

查看试题解析
10. 连接正八边形的三个顶点，得到如图所示的图形，下列说法错误的是（）

A、四边形 $A F G H$ 与四边形 $C F E D$ 的面积相等 B、连接 $B F$ ，则 $B F$ 分别平分 $∠ A F C$ 和 $∠ A B C$ C、整个图形是轴对称图形，但不是中心对称图形 D、 $Δ A C F$ 是等边三角形

查看试题解析

二、填空题

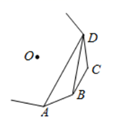
11. 如图，A、B、C、D为一个正多边形的相邻四个顶点，O为正多边形的中心，若∠ADB=12°，则这个正多边形的边数为

查看试题解析
12. 如图，正方形 $A B C D$ 和正六边形 $A E F C G H$ 均内接于 $⊙ O$ ，连接 $H D$ ；若线段 $H D$ 恰好是 $⊙ O$ 的一个内接正 $n$ 边形的一条边，则 $n =$ ．

查看试题解析
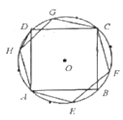13. 正六边形的边心距为 $\sqrt{3}$ ，则该正六边形的边长是.

查看试题解析
14. ⊙O的半径为 $2 cm$ ，则⊙O的内接正方形的面积是 ${cm}^{2}$ .

查看试题解析
15. 如图，四边形 $A B C D$ 为 $⊙ O$ 的内接正四边形， $△ A E F$ 为 $⊙ O$ 的内接正三角形，若 $D F$ 恰好是同圆的一个内接正 $n$ 边形的一边，则 $n$ 的值为．

查看试题解析
16. 如图，正 $△ A B C$ 内接于半径为1cm的圆，则阴影部分的面积为。

查看试题解析

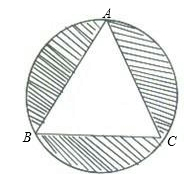
三、解答题

17. 如图，已知正三角形ABC内接于 $⊙ O$ ，AD是 $⊙ O$ 的内接正十二边形的一条边长，连接CD，若 $C D = 6 \sqrt{2} c m$ ，求 $⊙ O$ 的半径．

查看试题解析
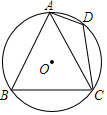18. 如图，四边形ABCD是⊙O的内接正方形，若正方形的面积等于4，求⊙O的面积．

查看试题解析
19. 如图五边形ABCDE内接于⊙O，∠A =∠B=∠C=∠D=∠E．
求证：五边形ABCDE是正五边形

查看试题解析
20. 如图，已知正n边形边长为a，边心距为r，求正n边形的半径R、周长P和面积S．

查看试题解析
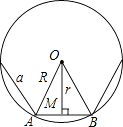21. 如图，正三角形ABC内接于⊙O，若AB= $2 \sqrt{3}$ cm，求⊙O的半径．

查看试题解析
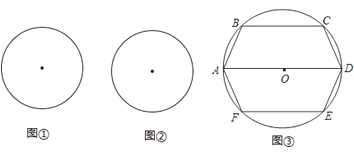
22.
如图，圆O的半径为r．
（1）在图①中，画出圆O的内接正△ABC，简要写出画法；求出这个正三角形的周长．
（2）在图②中，画出圆O的内接矩形ABCD，简要写出画法；若设AB=x，求出矩形的周长.
（3）如图③，六边形ABCDEF内接于半径为r（常数）的⊙O，其中AD为直径，且AB=CD=DE=FA．设AB=x，求六边形ABCDEF的周长L关于x的函数关系式，并探究L是否有最大值，若有，请指出x为何值时，L取得最大值；若没有，请说明理由．

查看试题解析
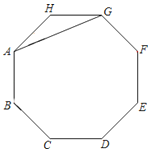
23.
如图，AG是正八边形ABCDEFGH的一条对角线．
（1）在剩余的顶点B、C、D、E、F、H中，连接两个顶点，使连接的线段与AG平行，并说明理由；
（2）两边延长AB、CD、EF、GH，使延长线分别交于点P、Q、M、N，若AB=2，求四边形PQMN的面积．

查看试题解析

四、综合题

24. 圆周率 $π$ 的故事
我国古代数学家刘徽通过“割圆术”来估计圆周率 $π$ 的值——“割之弥细，所失弥少，割之又割，以至于不可割，则与圆合体，而无所失矣”，可以理解为当正多边形的边数越来越多时，该正多边形与它的外接圆越来越“接近”，这样就可以用正多边形的周长替代它的外接圆的周长，从而估算出圆周率 $π$ 的值.

(1)、对于边长为a的正方形，其外接圆半径为，根据故事中的方法，用该正方形的周长4a替代它的外接圆周长，利用公式 $C = 2 π r$ ，可以估算 $π = \frac{C}{2 r} =$ .

(2)、类比（1），当正多边形为正六边形时，估计 $π$ 的值.

查看试题解析