初中数学浙教版九年级上册3.6 圆内接四边形同步练习
试卷更新日期：2021-08-12 类型：同步测试
一、单选题
-
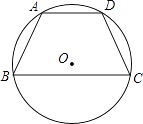
1. 如图，已知四边形ABCD内接于⊙O，∠ABC=70°，则∠ADC的度数是（ ）
A、70° B、110° C、130° D、140°2. 已知圆内接四边形 中， ，则 （ ）A、 B、 C、 D、3. 已知圆内接四边形ABCD中，∠A：∠B：∠C=1：2：3，则∠D的大小是（ ）A、45° B、60° C、90° D、135°4. 如图，四边形ABCD为圆内接四边形∠A=85°，∠B=105°，则∠C的度数为（ ）
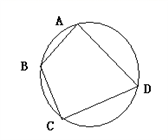A、115° B、75° C、95° D、无法求5. 如图；四边形 的四个顶点均在半圆O上，若 ，则 （ ）
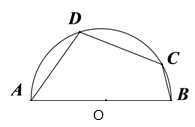A、130° B、120° C、125° D、110°6. 如图，四边形 内接于⊙O，若 ，则 的度数为（ ）
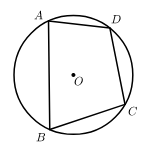A、18 B、72 C、100 D、1087. 若四边形ABCD是圆内接四边形，则它的内角 ， ， ， 的度数之比可能是（ ）A、3：1：2：5 B、1：2：2：3 C、2：7：3：6 D、1：2：4：38. 圆内接四边形ABCD，∠A，∠B，∠C的度数之比为3∶4∶6，则∠D的度数为( )A、60° B、80° C、100° D、120°9. 四边形ABCD内接于☉O，若2∠A+3∠C，则∠A=（ ）A、45° B、72° C、108° D、135°10. 如图，四边形ABCD内接于⊙O，E为CD延长线上一点，若∠ADE=110°，则∠B=（ ）
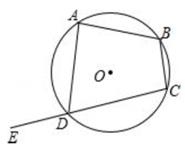A、80° B、100° C、110° D、120°二、填空题
-
11. 已知正四边形的外接圆的半径为2，则正四边形的周长是12. 如图，四边形ABCD内接于⊙O，若∠ADC＝120°，则∠AOC的度数为.
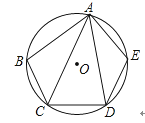
13.如图，在⊙O的内接五边形ABCDE中，∠CAD=35°，则∠B+∠E= .
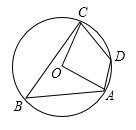
14. 如图，四边形 是平行四边形， 经过点A ， C ， D与 交于点E ， 连接 ，若 ，则 ．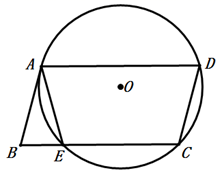
15. 如图，四边形 内接于 ， 、 的延长线相交于点 ， 、 的延长线相交于点 .若 ， ，则 °.
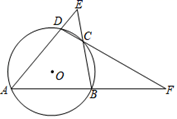16. 如图，四边形ABCD为圆的内接四边形，DA，CB的延长线交于点P，∠P＝30°，∠ABC＝100°，则∠C＝ .
三、解答题
-
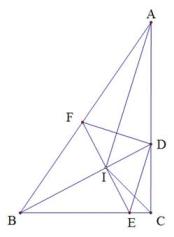
17. 如图，在三角形ABC中， ∠ C=90°，I是内心，直线BI与AC交于点D，过点D作DE//AI与BC交于点E，直线EI与AB交于点F.证明：DF ⊥ AI.
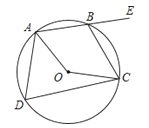
18. 如图，四边形ABCD是 的内接四边形，DB=DC求证：∠CAD=∠EAD．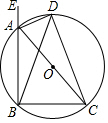
19. 如图，⊙ 的内接四边形ABCD两组对边的延长线分别相交于点E、F。
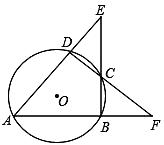(1)、若∠E=∠F时，求证：∠ADC=∠ABC；(2)、若∠E=∠F=42°时，求∠A的度数；(3)、若∠E=α，∠F=β，且。α≠β.请你用含有α、β的代数式表示∠A的大小.20. 如图，四边形ABCD是⊙O的内接四边形，BC的延长线与AD的延长线交于点E，且DC=DE．
(1)、求证：∠A=∠AEB．(2)、连接OE，交CD于点F，OE⊥CD．求证：△ABE是等边三角形．21. 如图，四边形ABCD内接于⊙O，AD∥BC，求证：AB=CD．
