初中数学浙教版九年级上册3.5 圆周角同步练习
试卷更新日期:2021-08-12 类型:同步测试
一、单选题
-
1. 如图,点 , , 在⊙O上, ,则 的度数为( )
 A、 B、 C、 D、2. 如图, 为 的直径, 是 的弦, ,则 的度数为( )
A、 B、 C、 D、2. 如图, 为 的直径, 是 的弦, ,则 的度数为( ) A、 B、 C、 D、3. 如图, , 是 上直径 两侧的两点.设 ,则 ( )
A、 B、 C、 D、3. 如图, , 是 上直径 两侧的两点.设 ,则 ( ) A、 B、 C、 D、4. 如图,四边形 内接于 ,点 为边 上任意一点(点 不与点 , 重合)连接 .若 ,则 的度数可能为( )
A、 B、 C、 D、4. 如图,四边形 内接于 ,点 为边 上任意一点(点 不与点 , 重合)连接 .若 ,则 的度数可能为( )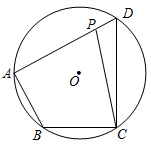 A、 B、 C、 D、5. 如图, 是 的直径, 是弦(点C不与点A , 点B重合,且点C与点D位于直径 两侧),若 ,则 等于( )
A、 B、 C、 D、5. 如图, 是 的直径, 是弦(点C不与点A , 点B重合,且点C与点D位于直径 两侧),若 ,则 等于( )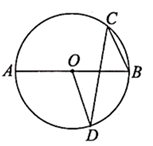 A、 B、 C、 D、6. 如图, 是⊙O的直径, 、 是⊙O上的两点, ,则 的度数为( )
A、 B、 C、 D、6. 如图, 是⊙O的直径, 、 是⊙O上的两点, ,则 的度数为( ) A、60° B、65° C、70° D、75°7. 如图, 的弦 、 的延长线交圆外于点 ,若 , ,则 的大小是( )
A、60° B、65° C、70° D、75°7. 如图, 的弦 、 的延长线交圆外于点 ,若 , ,则 的大小是( )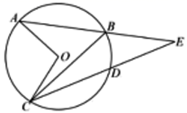 A、20° B、25° C、30° D、50°8. 如图,AB为⊙O的直径,点C , D在⊙O上.若∠AOD=30°,则∠BCD的度数是( )
A、20° B、25° C、30° D、50°8. 如图,AB为⊙O的直径,点C , D在⊙O上.若∠AOD=30°,则∠BCD的度数是( ) A、100° B、105° C、110° D、120°9. 如图,在△ABC中,以AB为直径作⊙O , 交AC于点E , 交BC于点D , 若CD=BD , 则( )
A、100° B、105° C、110° D、120°9. 如图,在△ABC中,以AB为直径作⊙O , 交AC于点E , 交BC于点D , 若CD=BD , 则( ) A、AC=BC B、 C、AB=2DE D、BC•BD=AB•CE10. 如图, 与 是 的两条互相垂直的弦,交点为点 , ,点 在圆上,则 的度数为( )
A、AC=BC B、 C、AB=2DE D、BC•BD=AB•CE10. 如图, 与 是 的两条互相垂直的弦,交点为点 , ,点 在圆上,则 的度数为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 已知一条弧所对的圆心角为 80°,则这条弧所对的圆周角度数为°.12. 如图,在 中, 为 直径, 为圆上一点,若 ,则 的度数为 .
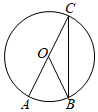 13. 如图, 是 的外接圆,连接 并延长交 于点 ,若 ,则 的度数为.
13. 如图, 是 的外接圆,连接 并延长交 于点 ,若 ,则 的度数为.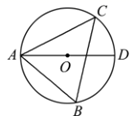 14. 如图所示的网格是正方形网格, , , , 是网格线交点, 恰好经过点 , , ,OD为与网格线重合的一条半径,则∠ABC 与∠AOD大小关系为:∠ABC ∠AOD(填“>”,“=”或“<”).
14. 如图所示的网格是正方形网格, , , , 是网格线交点, 恰好经过点 , , ,OD为与网格线重合的一条半径,则∠ABC 与∠AOD大小关系为:∠ABC ∠AOD(填“>”,“=”或“<”).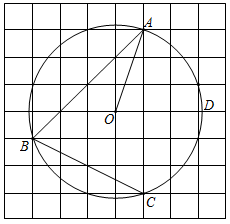 15. 如图, 是⊙O的直径, 是直径 两侧⊙O上的点,若 ,那么 的度数为°.
15. 如图, 是⊙O的直径, 是直径 两侧⊙O上的点,若 ,那么 的度数为°.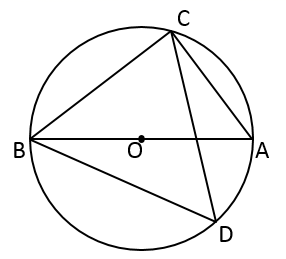 16. 如图,AD是⊙O的直径, = ,若∠AOB=36°,则圆周角∠BPC的度数是.
16. 如图,AD是⊙O的直径, = ,若∠AOB=36°,则圆周角∠BPC的度数是.
三、解答题
-
17. 已知:如图,在⊙O中,AB=CD,AB与CD相交于点M.
求证:AM=DM.
 18. 如下是小华设计的“作 的角平分线”的尺规作图过程,请帮助小华完成尺规作图并填空(保留作图痕迹).
18. 如下是小华设计的“作 的角平分线”的尺规作图过程,请帮助小华完成尺规作图并填空(保留作图痕迹).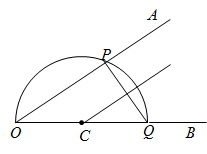
步骤
作法
推断
第一步
在 上任取一点C , 以点C为圆心, 为半径作半圆,分别交射线 于点P , 点Q , 连接
▲ ,理由是 ▲
第二步
过点C作 的垂线,交 于点D , 交 于点E
, ③
第三步
作射线
射线 平分
射线 为所求作.
19. 如图,AB是⊙O直径,弦CD与AB相交与点E , ∠ADC=26°,求∠CAB的度数.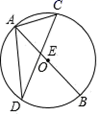 20. 如图, 内接于 , , ,则 的直径等于多少?
20. 如图, 内接于 , , ,则 的直径等于多少?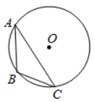 21. 如图,AB是⊙O的直径,C,D,E是⊙O上的点,若 = ,∠E=70°,求∠ABC的度数.
21. 如图,AB是⊙O的直径,C,D,E是⊙O上的点,若 = ,∠E=70°,求∠ABC的度数. 22. 用两种方法证明“圆的内接四边形对角互补”.
22. 用两种方法证明“圆的内接四边形对角互补”.已知:如图①,四边形ABCD内接于⊙O.
求证:∠B+∠D=180°.


证法1:如图②,作直径DE交⊙O于点E,连接AE、CE.
∵DE是⊙O的直径,
∴( ).
∵∠DAE+∠AEC+∠DCE+∠ADC=360°,
∴∠AEC+∠ADC=360°-∠DAE-∠DCE=360°-90°-90°=180°.
∵∠B和∠AEC所对的弧是 ,
∴( ).
∴∠B+∠ADC=180°.
请把证法1补充完整,并用不同的方法完成证法2.
证法2:
23. 如图,PA,PB分别与⊙O相切于A,B点,C为⊙O上一点,∠P=66°,求∠C.
四、综合题
-
24. 如图①,将一块含30°角的三角板和一个量角器拼在一起,如图②是拼接示意图,三角板斜边AB与量角器所在圆的直径MN重合且∠CAB=30°,其量角器最外缘的读数是从N点开始(即N点的读数为0),现有射线CP绕点C从CA的位置开始按顺时针方向以每秒2度的速度旋转到CB位置,在旋转过程中,射线CP与量角器的半圆弧交于点E.
 (1)、当旋转7.5秒时,连结BE,E点处量角器上的读数为度;(2)、在(1)的条件下求证BE=CE;(3)、设旋转x秒后,E点处量角器上的读数为y度,写出y与x的函数表达式.
(1)、当旋转7.5秒时,连结BE,E点处量角器上的读数为度;(2)、在(1)的条件下求证BE=CE;(3)、设旋转x秒后,E点处量角器上的读数为y度,写出y与x的函数表达式.