初中数学浙教版九年级上册3.2 图形的旋转同步练习
试卷更新日期:2021-08-12 类型:同步测试
一、单选题
-
1. 将如图所示的图形绕中心按顺时针方向旋转60°后可得到的图形是( )
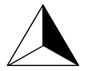 A、
A、 B、
B、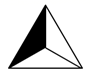 C、
C、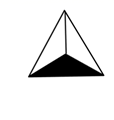 D、
D、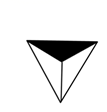 2. 如图,在方格纸中,将 绕点 按顺时针方向旋转90°后得到 ,则下列四个图形中正确的是( )
2. 如图,在方格纸中,将 绕点 按顺时针方向旋转90°后得到 ,则下列四个图形中正确的是( )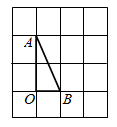 A、
A、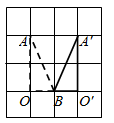 B、
B、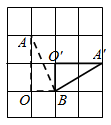 C、
C、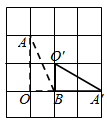 D、
D、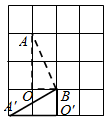 3. 如图,在 中, , ,将 绕点C顺时针旋转90°得到 ,点B的对应点 在边 上(不与点A , C重合),则 的度数为( )
3. 如图,在 中, , ,将 绕点C顺时针旋转90°得到 ,点B的对应点 在边 上(不与点A , C重合),则 的度数为( )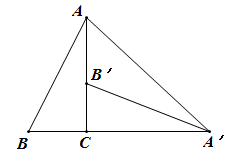 A、 B、 C、 D、4. 如图,在△ABC中,∠ACB=90°,将△ABC绕点C逆时针旋转得到△A1B1C1 , 此时点A的对应点A1恰好在AB边上,点B的对应点为B1 , 则下列结论一定正确的是( )
A、 B、 C、 D、4. 如图,在△ABC中,∠ACB=90°,将△ABC绕点C逆时针旋转得到△A1B1C1 , 此时点A的对应点A1恰好在AB边上,点B的对应点为B1 , 则下列结论一定正确的是( )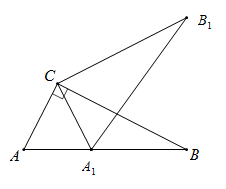 A、AB=B1C B、CA1=A1B C、A1B1⊥BC D、∠CA1A=∠CA1B15. 如图,在 中, ,在同一平面内,将 绕点A旋转到 的位置,使得 ,则 的度数为( )
A、AB=B1C B、CA1=A1B C、A1B1⊥BC D、∠CA1A=∠CA1B15. 如图,在 中, ,在同一平面内,将 绕点A旋转到 的位置,使得 ,则 的度数为( )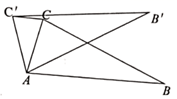 A、30° B、35° C、40° D、50°6. 如图,在 中, ,将 绕点C逆时针旋转得到 ,点A,B的对应点分别为D,E,连接 .当点A,D,E在同一条直线上时,下列结论一定正确的是( )
A、30° B、35° C、40° D、50°6. 如图,在 中, ,将 绕点C逆时针旋转得到 ,点A,B的对应点分别为D,E,连接 .当点A,D,E在同一条直线上时,下列结论一定正确的是( )
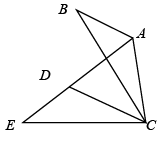 A、 B、 C、 D、7. 如图.将 绕点 按顺时针方向旋转20°, 点落在 位置,点 落在 位置,若 ,则 的度数为( )
A、 B、 C、 D、7. 如图.将 绕点 按顺时针方向旋转20°, 点落在 位置,点 落在 位置,若 ,则 的度数为( )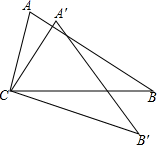 A、45° B、60° C、70° D、90°8. 如图,在平面直角坐标系 中,四边形 是正方形,点 ,点D是 中点,将 以C为旋转中心逆时针旋转 后,再将得到的三角形平移,使点C与点O重合,写出此时点D的对应点的坐标( )
A、45° B、60° C、70° D、90°8. 如图,在平面直角坐标系 中,四边形 是正方形,点 ,点D是 中点,将 以C为旋转中心逆时针旋转 后,再将得到的三角形平移,使点C与点O重合,写出此时点D的对应点的坐标( )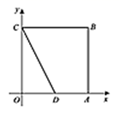 A、 B、 C、 D、9. 如图,以点 为旋转中心,把 顺时针旋转得 .记旋转角为 ,连接AE, 为 ,则 的度数为( )
A、 B、 C、 D、9. 如图,以点 为旋转中心,把 顺时针旋转得 .记旋转角为 ,连接AE, 为 ,则 的度数为( )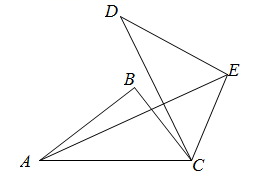 A、 B、 C、 D、10. 如图,在 中, ,将 绕点 逆时针旋转得到 ,此时使点 的对应点 恰好在 边上,点 的对应点为 , 与 交于点 ,则下列结论一定正确的是( )
A、 B、 C、 D、10. 如图,在 中, ,将 绕点 逆时针旋转得到 ,此时使点 的对应点 恰好在 边上,点 的对应点为 , 与 交于点 ,则下列结论一定正确的是( )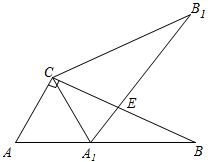 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 如图,将 绕点 逆时针旋转70°到 的位置,若 ,则 .
 12. 如图,正五边形 的边 在直线 上,现将其绕点 按顺时针方向旋转一定角度,使五边形的边 的对应边 落在直线 上,则正五边形旋转的最小角度是°.
12. 如图,正五边形 的边 在直线 上,现将其绕点 按顺时针方向旋转一定角度,使五边形的边 的对应边 落在直线 上,则正五边形旋转的最小角度是°.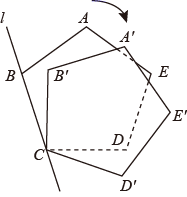 13. 如图,在平面直角坐标系中,点 的坐标为 ,点 的坐标为 ,连接 ,若将 绕点 顺时针旋转 ,得到 ,则点 的坐标为 .
13. 如图,在平面直角坐标系中,点 的坐标为 ,点 的坐标为 ,连接 ,若将 绕点 顺时针旋转 ,得到 ,则点 的坐标为 .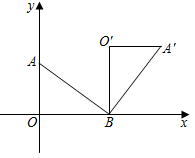 14. 如图,正方形 的边长为2,点 在 轴的正半轴上,点 在 轴的负半轴上,将正方形 绕点 逆时针旋转30°至正方形 的位置, 与 相交于点 ,则点 的坐标为 .
14. 如图,正方形 的边长为2,点 在 轴的正半轴上,点 在 轴的负半轴上,将正方形 绕点 逆时针旋转30°至正方形 的位置, 与 相交于点 ,则点 的坐标为 .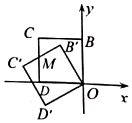 15. 如图,将△ABC纸片绕点C顺时针旋转40°得到△A'B'C,连接AA',若AC⊥A'B',则∠AA'B'的度数为.
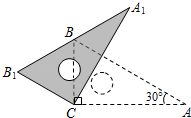
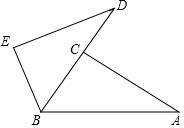
15. 如图,将△ABC纸片绕点C顺时针旋转40°得到△A'B'C,连接AA',若AC⊥A'B',则∠AA'B'的度数为.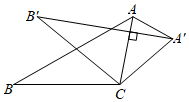 16. 将一副三角板中的两个直角顶点C叠放在一起,其中 , , .若按住三角板 不动,绕顶点C转动三角板DCE , 在旋转过程中始终要求点E在直线BC上方,当三角板DCE运动中,有一边和AB平行时,则 的度数为 .
16. 将一副三角板中的两个直角顶点C叠放在一起,其中 , , .若按住三角板 不动,绕顶点C转动三角板DCE , 在旋转过程中始终要求点E在直线BC上方,当三角板DCE运动中,有一边和AB平行时,则 的度数为 .
三、解答题
-
17. 如图,在三角板ABC中,∠ACB=90°,∠A=30°,AC=6,将三角板ABC绕点C逆时针旋转,当起始位置时的点B恰好落在边A1B1上时,求A1B的长
 18. 如图,正方形OABC绕着点O逆时针旋转40°得到正方形ODEF,连接AF,求∠OFA的度数
18. 如图,正方形OABC绕着点O逆时针旋转40°得到正方形ODEF,连接AF,求∠OFA的度数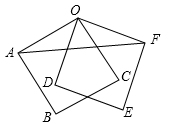 19. 如图,已知△ 和点 。
19. 如图,已知△ 和点 。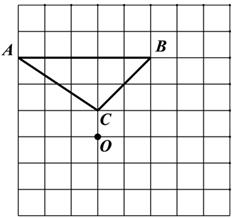 (1)、把△ 绕点 顺时针旋转90°得到△ ,在网格中画出△ ;(2)、用直尺和圆规作△ 的边 , 的垂直平分线,并标出两条垂直平分线的交点 (要求保留作图痕迹,不写作法);指出点 是△ 的内心,还是外心?20. 如图在△ABC中,AB=BC,将△ABC绕点A沿顺时针方向旋转得△AB1C1 , 使点C1落在直线BC上(点C1与点C不重合),求证:AB1∥CB.
(1)、把△ 绕点 顺时针旋转90°得到△ ,在网格中画出△ ;(2)、用直尺和圆规作△ 的边 , 的垂直平分线,并标出两条垂直平分线的交点 (要求保留作图痕迹,不写作法);指出点 是△ 的内心,还是外心?20. 如图在△ABC中,AB=BC,将△ABC绕点A沿顺时针方向旋转得△AB1C1 , 使点C1落在直线BC上(点C1与点C不重合),求证:AB1∥CB. 21. 已知:如图,在 中, ,将 绕点B按逆时针方向旋转 得到 ,点C在边BD上.
21. 已知:如图,在 中, ,将 绕点B按逆时针方向旋转 得到 ,点C在边BD上.求: 的度数.
 22. 在直角坐标系中,我们把横、纵坐标都为整数的点称为整点,记顶点都是整点的四边形为整点四边形.如图,已知整点A(1,2),B(3,4),请在所给网格上按要求画整点四边形.
22. 在直角坐标系中,我们把横、纵坐标都为整数的点称为整点,记顶点都是整点的四边形为整点四边形.如图,已知整点A(1,2),B(3,4),请在所给网格上按要求画整点四边形.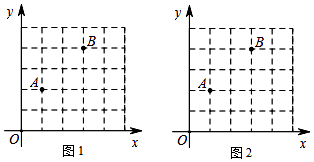 (1)、在图1中画一个四边形OABP,使得点P的横、纵坐标之和等于5.(2)、在图2中画一个四边形OABQ,使得点Q的横、纵坐标的平方和等于20.23. 如图,在平面直角坐标系中,三角形②、③是由三角形①依次旋转后所得的图形.
(1)、在图1中画一个四边形OABP,使得点P的横、纵坐标之和等于5.(2)、在图2中画一个四边形OABQ,使得点Q的横、纵坐标的平方和等于20.23. 如图,在平面直角坐标系中,三角形②、③是由三角形①依次旋转后所得的图形.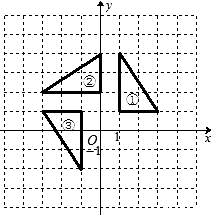 (1)、在图中标出旋转中心P的位置,并写出它的坐标;(2)、在图上画出再次旋转后的三角形④.
(1)、在图中标出旋转中心P的位置,并写出它的坐标;(2)、在图上画出再次旋转后的三角形④.四、综合题
-
24. 在平面直角坐标系中,△ABC的顶点坐标分别是A(2,4)、B(1,2)、C(5,3),如图:
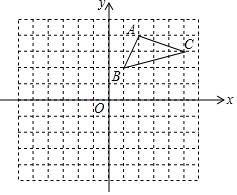
(1)以点(0,0)为旋转中心,将△ABC顺时针转动90°,得到△A1B1C1 , 在坐标系中画出△A1B1C1 , 写出A1、B1、C1的坐标;
(2)在(1)中,若△ABC上有一点P(m,n),直接写出对应点P1的坐标.
(3)作出△ABC关于点O的中心对称图形△A2B2C2.