初中数学浙教版九年级上册第三章 圆的基本性质单元测试
试卷更新日期:2021-08-12 类型:单元试卷
一、单选题
-
1. 如图,已知长方形 中, ,圆B的半径为1,圆A与圆B内切,则点 与圆A的位置关系是( )
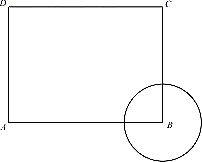 A、点C在圆A外,点D在圆A内 B、点C在圆A外,点D在圆A外 C、点C在圆A上,点D在圆A内 D、点C在圆A内,点D在圆A外
A、点C在圆A外,点D在圆A内 B、点C在圆A外,点D在圆A外 C、点C在圆A上,点D在圆A内 D、点C在圆A内,点D在圆A外 -
2. 如图,AB是⊙O的直径,点C是⊙O上一点,连接AC,BC,则∠C的度数是( )
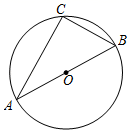 A、60° B、90° C、120° D、150°
A、60° B、90° C、120° D、150° -
3. 如图,⊙O是正五边形ABCDE的外接圆,则正五边形的中心角∠AOB的度数是( )
 A、72° B、60° C、54° D、36°
A、72° B、60° C、54° D、36° -
4. 4张扑克牌如图1所示放在桌子上,小明将其中一张旋转180°后得到的图如图2所示,那么他旋转的牌从左起是( ).
 A、第一张 B、第二张 C、第三张 D、第四张
A、第一张 B、第二张 C、第三张 D、第四张 -
5. 学习圆的性质后,小铭与小熹就讨论起来,小铭说:“被直径平分的弦也与直径垂直”,小熹说:“用反例就能说明这是假命题” .下列判断正确的是( )A、两人说的都对 B、小铭说的对,小燕说的反例不存在 C、两人说的都不对 D、小铭说的不对,小熹说的反例存在
-
6. 如图,在 中, 为直径, 为弦,已知 ,则 的度数为( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
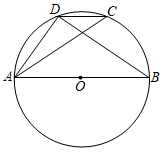
7. 如图,四边形ABCD内接于⊙O,AB为直径,∠C=120°,若AD=2,则AB的长为( )
 A、 B、2 C、2 D、4
A、 B、2 C、2 D、4 -
8. 如图,四边形ABCD为⊙O的内接正四边形,△AEF为⊙O的内接正三角形,若DF恰好是同圆的一个内接正n边形的一边,则n的值为( )
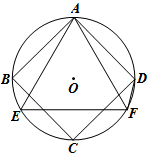 A、8 B、10 C、12 D、15
A、8 B、10 C、12 D、15 -
9. 如图,等边 的三个顶点都在 上, 是 的直径.若 ,则劣弧 的长是( )
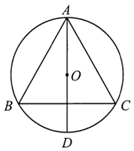 A、 B、 C、 D、
A、 B、 C、 D、 -
10. 如图,正六边形 的边长为6,以顶点A为圆心, 的长为半径画圆,则图中阴影部分的面积为( )
 A、 B、 C、 D、
A、 B、 C、 D、
二、填空题
-
11. 如图,在⊙O内接四边形 中,若 ,则 .
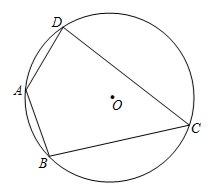
-
12. 点 是非圆上一点,若点 到 上的点的最小距离是 ,最大距离是 ,则 的半径是 .
-
13. 如图,已知⊙O半径为5,弦AB长为8,点P为弦AB上一动点,连结OP,则线段OP的最小长度是.

-
14. 如图所示,在⊙O中,直径MN=10,正方形ABCD的四个顶点分别在PM以及⊙O的半径OM,OP上,并且∠POM=45°,则AB的长为 .

-
15. 如图,正五边形 内接于 ,点 在弧 上,则 的度数为

-
16. 如图,AB是 的直径,分别以点A和点B为圆心、AB长为半径作圆弧,两弧交于点C和点D.若 ,则图中阴影部分图形的周长和为 . (结果保留 )

三、解答题
-
17. 如图: ,CD⊥OA于D,CE⊥OB于E,求证:CD=CE.
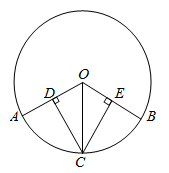
-
18. 如图,沿一条母线将圆锥侧面剪开并展平,得到一个扇形,若圆锥的底面圆的半径 ,扇形的圆心角 ,求该圆锥的母线长 .

-
19. 如图,已知圆O内接正六边形 的边长为 ,求这个正六边形的边心距n , 面积S .
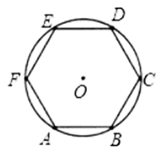
-
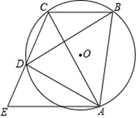
20. 如图,四边形 内接于 , 与 为对角线, ,过点A作 交 的延长线于点E.求证: .
-
21. 如图, 是 的直径,弦 与 相交于点 .求 的度数.

-
22. 如图AB是⊙O的直径,弦CD⊥AB于点E,若EB=9,AE=1,求弦CD的长.

-
23. 如图,在等边△ABC中,AB=6,点D是线段BC上的一点,CD=4,将△ABD绕点A旋转后得到△ACE , 连接CE . 求CE的长.

四、综合题
-
24. 如图
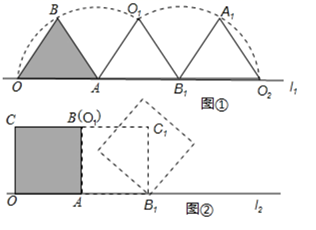
如图①,小慧同学把一个等边三角形纸片(即△OAB)放在直线l1上,OA边与直线l1重合,然后将三角形纸片绕着顶点A按顺时针方向旋转120°,此时点O运动到了点O1处,点B运动到了点B1处;小慧又将三角形纸片AO1B1绕B1点按顺时针方向旋转120°,点A运动到了点A1处,点O1运动到了点O2处(即顶点O经过上述两次旋转到达O2处).
小慧还发现:三角形纸片在上述两次旋转过程中,顶点O运动所形成的图形是两段圆弧,即弧OO1和弧O1O2 , 顶点O所经过的路程是这两段圆弧的长度之和,并且这两段圆弧与直线l1围成的图形面积等于扇形AOO1的面积、△AO1B1的面积和扇形B1O1O2的面积之和.
小慧进行类比研究:如图②,她把边长为1的正方形纸片OABC放在直线l2上,OA边与直线l2重合,然后将正方形纸片绕着顶点A按顺时针方向旋转90°,此时点O运动到了点O1处(即点B处),点C运动到了点C1处,点B运动到了点B1处;小慧又将正方形纸片AO1C1B1绕B1点按顺时针方向旋转90°,……,按上述方法经过若干次旋转后,她提出了如下问题:
(1)、若正方形纸片OABC按上述方法经过3次旋转,求顶点O经过的路程,并求顶点O在此运动过程中所形成的图形与直线l2围成图形的面积;若正方形OABC按上述方法经过5次旋转,求顶点O经过的路程;(2)、正方形纸片OABC按上述方法经过多少次旋转,顶点O经过的路程是 ?
