初中数学浙教版八年级上册4.1 探索确定位置的方法同步练习

试卷更新日期：2021-08-12 类型：同步测试

进入 出卷网 下载

一、单选题

  • 1. 确定平面直角坐标系内点的位置是（     ）
    A、一个实数 B、一个整数 C、一对实数 D、有序实数对

    查看试题解析

  • 2. 下列数据能确定物体具体位置的是（    ）
    A、明华小区东 B、希望路右边 C、东经118°，北纬28° D、北偏东30°

    查看试题解析

  • 3. 如图，雷达探测器发现了A，B，C，D，E，F六个目标.目标C，F的位置分别表示为C（6，120°），F（5，210°），按照此方法表示目标A，B，D，E的位置时，其中表示正确的是（   ）

    A、A（4，30°） B、B（1，90°） C、D（ 4，240°） D、E（3，60°）

    查看试题解析

  • 4. 如图，若“马”所在的位置的坐标为（-2，-1），“象”所在位置的坐标为（-1，1），则“兵”所在位置的坐标为（  ）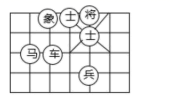

    A、（-2，1） B、（-2，2） C、（1，-2） D、（2，-2）

    查看试题解析

  • 5. 如图中的一张脸，小明说：“如果我用 (0 ， 2) 表示左眼，用 (2 ， 2) ）表示右眼”，那么嘴的位置可以表示成（   ）

    A、(0 ， 1) B、(0 ， 0) C、(1 ， −1) D、(1 ， 0)

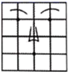    查看试题解析

  • 6. 2021年是中国共产党建党100周年暨红军长征胜利85周年．长征是中国共产党和中国革命事业从挫折走向胜利的伟大转折点．如图是红一方面军长征路线图，如果表示瑞金的点的坐标为（4，﹣3），表示遵义会议的点的坐标为（ 12 ，﹣2），那么表示吴起镇会师的点的坐标为（ ）

    A、（3，0） B、（0，3） C、（3，1） D、（1，3）

    查看试题解析

  • 7. 如图是老北京城一些地点的分布示意图，在图中，分别以正东，正北方向为 x 轴， y 轴的正方向建立平面直角坐标系．如果表示东直门的点的坐标为（3.5，4），表示宣武门的点的坐标为（－2，－1），那么坐标原点所在的位置是（　　）

    A、天安门 B、正阳门 C、西直门 D、阜成门

    查看试题解析

  • 8. 如图是雷达探测到的6个目标，若目标C用（40，120°）表示，目标D用（50，210°）表示，则（30，240°）表示的目标是（    ）

    A、目标A B、目标B C、目标F D、目标E

    查看试题解析

  • 9. 如图是某市市内简图（图中每个小正方形的边长为1个单位长度），如果文化馆的位置是 (−2 ， 1) ，超市的位置是 (3 ， −3) ，则市场的位置是（    ）

    A、(−3 ， 3) B、(3 ， 2) C、(−1 ， −2) D、(5 ， 3)

    查看试题解析

  • 10. 下图是利用平面直角坐标系画出的首钢园中部分场馆建筑的分布图，若这个坐标系分别以正东、正北方向为 x 轴、 y 轴的正方向，表示群明湖的点的坐标为 (−2 ， 0) ，表示冰壶馆的点的坐标为 (−3 ， 2) ，则表示下列场馆建筑的点的坐标正确的是（    ）

    A、滑雪大跳台 (−5 ， 0) B、五一剧场 (−3 ， −2) C、冬奥组委会 (−5 ， 4) D、全民畅读艺术书店 (5 ， 0)

    查看试题解析

二、填空题

  • 11. 2021年4月8日，中国扬州世界园艺博览会在扬州仪征市开幕，本届搏览会以“绿色城市，健康生活”为主题.如图，是扬州世界园艺博览会部分导游图，若滩涂印象的坐标为 (2 ， 1) ，丛林野趣的坐标为 (−3 ， −2) ，则中国馆的坐标为.

    查看试题解析

  • 12. 如果座位表上“5列2行”记作 (5 ， 2) ，那么“4列3行”记为.

    查看试题解析

  • 13. 如图，某小区有古树 3 棵，分别记作为 M ，  N ，  P ， 若建立平面直角坐标系，将古树 M ，  N 用坐标分别表示为 (1 ，  1) 和  (2 ，  4) ，则古树 P 用坐标表示为

    查看试题解析

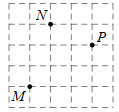  • 14. 如表是一组密码的一部分，目前已破译出“守初心”的对应口令是“担使命”，根据上述破译方法，破译出“找差距”的对应口令是.

    落

    市

    担

    山

    七

    牢

    七

    中

    湖

    为

    就

    吴

    命

    金

    使

    差

    圾

    守

    立

    实

    华

    人

    忘

    兴

    水

    分

    是

    心

    抓

    初

    成

    民

    银

    垃

    距

    共

    青

    祝

    区

    类

    年

    记

    庆

    找

    周

    和

    国

    州

    绿

    查看试题解析

  • 15. 如图所示为象棋盘的一部分，若“帅”位于点（2， - 1）上，“相”位于点（4， - 1）上，则“炮”所在的点的坐标是 .

    查看试题解析

  • 16. 如图，已知雷达探测器在一次探测中发现了两个目标，A、B，其中A的位置可以表示成 (60° ， 6) ，那么B可以表示为.

    查看试题解析

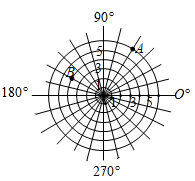
三、解答题

  • 17. 古城黄州以其名胜古迹吸引了不少游客，从地图上看，较有名的六外景点在黄州城内的分布是∶东坡赤壁在市政府以西2km再往南3km处，黄冈中学在市政府以东1km处，宝塔公园在市政府以东3km处，鄂黄大桥在市政府以东7km再往北8km处，遗爱湖在市政府以东4km再往北4km处，博物馆在市政府以北2km再往西1km处．请画图表示出这六个景点的位置，并用坐标表示出来．

    查看试题解析

  • 18. 请在图中建立平面直角坐标系，使学校的坐标是 (2 ， 5) ，并写出儿童公园，医院，水果店，宠物店，汽车站的坐标.

    查看试题解析

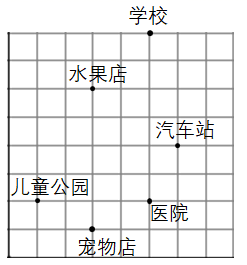  • 19. 如图是某个海岛的平面示意图，如果哨所1的坐标是（1，3），哨所2的坐标是（-2，0），请你先建立平面直角坐标系，并用坐标表示出小广场、雷达、营房、码头的位置．

    查看试题解析

  • 20. 如下图所示，从2街4巷到4街2巷，走最短的路线，共有几种走法？

    查看试题解析

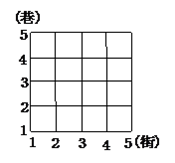  • 21. 如下图所示，A的位置为（2，6），小明从A出发，经（2，5）→（3，5）→（4，5）→（4，4）→（5，4）→（6，4），小刚也从A出发，经（3，6）→（4，6）→（4，7）→（5，7）→（6，7），则此时两人相距几个格?


    查看试题解析

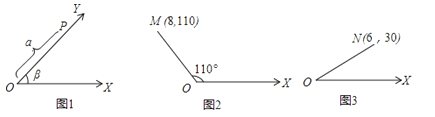
  • 22.

    如图1，将射线OX按逆时针方向旋转β角，得到射线OY，如果点P为射线OY上的一点，且OP=a，那么我们规定用（a，β）表示点P在平面内的位置，并记为P（a，β），例如，图2中，如果OM=8，∠XOM=110°，那么点M在平面内的位置，记为M（8，110），根据图形，解答下面的问题：

    （1）如图3，如果点N在平面内的位置记为N（6，30），那么ON各∠XON等于多少？

    （2）如果点A、B在平面内的位置分别记为A（5，30），B（12，120），试求A、B两点之间的距离并画出图．


    查看试题解析

  • 23. 五子连珠棋的棋盘是15行15列的正方形，规定黑子先下，双方交替进行，在任意一个方向上，先连成5个子的一方获胜，如图所示的是两人所下的棋局的一部分，A点的位置记作（8，3），执白子的一方若想再放一子便获胜，应该把子落在什么位置？

    查看试题解析

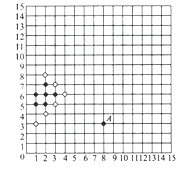
四、综合题

  • 24. 如图所示建立的平面直角坐标系中，标明了小刚家附近的一些地方．

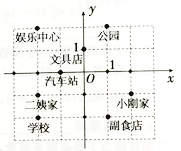    (1)、写出学校和文具店的坐标分别是 ， ；
    (2)、某星期日早晨，小刚从家里出发，沿 (1 ， −2) ， (−1 ， 0) ， (−2 ， −1) ， (−2 ， 2) ， (1 ， 2) ， (0 ， 1) 的路线转了一下，又回到家里，写出他路上经过的地方；
    (3)、连接他在（2）中路过的地点，你能说出它像什么吗？

    查看试题解析