吉林省梅河口市2020-2021学年高二下学期理数期末考试试卷

试卷更新日期：2021-08-12 类型：期末考试

进入出卷网下载

一、选择题（本题共12小题，每小题5分，共60分. 在每小题给出的四个选项中，只有一项是符合题目要求的）

1. 设 $A = {x \in N | - 1 \leq x < 7}$ ， $B = {x \in N_{+} | - 1 < x \leq 5}$ ，则 $∁_{A} B$ =（）

A、 ${0 ， 6}$ B、 ${- 1 ， 6}$ C、 ${0 ， 5 ， 6}$ D、 ${- 1 ， 6 ， 7}$

查看试题解析
2. 设 $x \in R$ ，则“ $x^{2} < 3 x$ ”是“ $\frac{1 - x}{x - 3} \geq 0$ ”的（）

A、充分而不必要条件 B、必要而不充分条件 C、充要条件 D、既不充分也不必要条件

查看试题解析
3. 下列4个函数中，定义域和值域均为 $(0 ， + \infty)$ 的是（）

A、 $y = x^{- 2}$ B、 $y = \ln x$ C、 $y = 2^{x}$ D、 $y = x^{- \frac{1}{2}}$

查看试题解析
4. 函数 $f (x) = \frac{x \ln x}{e^{x}}$ 的图象大致是（）

A、 B、 C、 D、

查看试题解析
5. 设随机变量 $X$ 服从二项分布 $X ~ B (n ， p)$ ，且 $E (X) = 1.6 ， D (X) = 1.28$ ，则 $p =$ （）

A、0.1 B、0.2 C、0.3 D、0.4

查看试题解析
6. 已知函数 $f (x) = {\begin{cases} 2^{- x} ， x \geq 1 \\ {log}_{3} (1 - x) ， x < 1 \end{cases}$ ，则 $f (f (\frac{2}{3}))$ 等于（）

A、3 B、2 C、1 D、 $\log_{3} 2$ 　

查看试题解析
7. 若函数 $f (x) = m x^{2} - x + m - 1$ 的两个零点一个大于1，一个小于1，则实数m的取值范围是（）

A、（0，1） B、（0，1] C、 $(- \infty ， 0] \cup (1 ， + \infty)$ D、 $(- \infty ， 0) \cup (1 ， + \infty)$

查看试题解析
8. 定积分 $\int_{0}^{\frac{3 π}{2}} \sin x d x =$ （）

A、2 B、1 C、0 D、-1

查看试题解析
9. 下列函数中，既是奇函数，又在 $(- \infty ， + \infty)$ 上单调递减的函数是（）

A、 $y = \lg （ \sqrt{x^{2} + 1} - x)$ B、 $y = 1 - x^{3}$ C、 $y = | x | (1 - 2 x)$ D、 $y = 2^{- x} + 1$

查看试题解析
10. 方程 $9^{x} - 3^{x + 2} + 8 = 0$ 的非零实数解为（）

A、 $3 \log_{2} 3$ B、 $2 \log_{3} 2$ C、 $2 \log_{2} 3$ D、 $3 \log_{3} 2$

查看试题解析
11. 已知定义域为 $(- \infty ， + \infty)$ 的偶函数满足条件 $f (1 - x) = f (1 + x)$ ，则下面给出的等式中不恒成立的是（）

A、 $f (x) = f (x + 2)$ B、 $f (x) = f (x + 3)$ C、 $f (x) = f (x + 4)$ D、 $f (x) = f (x + 6)$

查看试题解析
12. 若函数 $f (x) = x e^{x} - 2 m x + m$ 有且只有一个零点，实数 $m$ 的取值范围是（）

A、 $(- \infty ， 0]$ B、 ${e} \cup (- \infty ， 0)$ C、 ${\frac{1}{4 \sqrt{e}} ， e} \cup (- \infty ， 0]$ D、 ${\frac{1}{4 \sqrt{e}}} \cup (- \infty ， 0)$

查看试题解析

二、填空题(本题共4小题，每小题5分，共20分．将答案填在答题卡相应的位置上)

13. 曲线 $y = \frac{\ln x}{x}$ 在点 $(1 ， 0)$ 处的切线的方程为．

查看试题解析
14. 若函数 $f (x) = m + \frac{1}{3^{x} + 1}$ 是定义域为 $(- \infty ， + \infty)$ 的奇函数，则实数 $m =$ ．

查看试题解析
15. 若函数 $f (x) = a x^{3} + a x^{2} + x - 1$ 不存在极值点，则 $a$ 的取值范围是．

查看试题解析
16. 设函数 $f (x) = {\begin{cases} x^{3} - 3 x ， x \leq x_{0} \\ - x ， x > x_{0} \end{cases}$ . ① 若 $x_{0} = 0$ ，则 $f (x)$ 的最大值为；
② 若 $f (x)$ 有且只有2个零点，则实数 $x_{0}$ 的取值范围是.

查看试题解析

三、解答题(本大题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤)

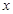17. 在直角坐标系中，曲线 $C_{1}$ 的参数方程为 ${\begin{cases} x = 2 \cos α \\ y = \sin α \end{cases}$ （ $α$ 是参数），以坐标原点为极点，轴正半轴为极轴建立极坐标系，曲线的极坐标方程为 $ρ = \frac{\sqrt{5}}{\sin θ - \cos θ}$ .

(1)、求 $C_{1}$ 的普通方程和的直角坐标方程；

(2)、判断与公共点的个数，并说明理由．

查看试题解析
18. 某同学大学毕业后，决定利用所学专业进行自主创业，经过市场调查，生产一小型电子产品需投入固定成本2万元，每生产 $x$ 万件，需另投入流动成本 $C (x)$ 万元，当年产量小于7万件时， $C (x) = \frac{1}{3} x^{2} + 2 x$ （万元）；当年产量不小于7万件时， $C (x) = 6 x + \ln x + \frac{e^{3}}{x} - 17$ （万元）.已知每件产品售价为6元，假设该同学生产的商品当年能全部售完.

(1)、写出年利润 $P (x)$ （万元）关于年产量 $x$ （万件）的函数解析式；（注：年利润=年销售收入-固定成本-流动成本）

(2)、当年产量约为多少万件时，该同学的这一产品所获年利润最大？最大年利润是多少？（取 $e^{3} = 20$ ）.

查看试题解析

19. 在迎来中国共产党成立100周年的重要时刻，我国脱贫攻坚战取得全面胜利，创造了又一个彪炳史册的人间奇迹.习近平总书记指出：“脱贫摘帽不是终点，而是新生活､新奋斗的起点.”为了解脱贫家庭人均年纯收入情况，某扶贫工作组对

A ， B

两个地区2019年脱贫家庭进行简单随机抽样，共抽取600户家庭作为样本，获得数据如下表：

	A地区	B地区
2019年人均年纯收入超过1万元	120户	200户
2019年人均年纯收入未超过1万元	180户	100户

假设所有脱贫家庭的人均年纯收入是否超过1万元相互独立.

(1)、分别从A地区和B地区2019年脱贫家庭中各随机抽取1户，记X为这2户家庭中2019年人均年纯收入超过1万元的户数，且把频率视作概率.求

X

的分布列和数学期望；

(2)、从样本中A地区的300户脱贫家庭中随机抽取4户，发现这4户家庭2020年人均年纯收入都超过1万元.根据这个结果，能否认为样本中A地区2020年人均年纯收入超过1万元的户数相比2019年有变化？请说明理由.

参考数据： $\frac{C_{120}^{4}}{C_{300}^{4}} \approx 0.025 ， \frac{C_{180}^{4}}{C_{300}^{4}} \approx 0.128$ .

查看试题解析

20. 已知函数 $f (x) = \lg (a x^{2} + 2 a x + 1)$ 的定义域为 $R$ .

(1)、求 $a$ 的取值范围；

(2)、若 $a > 0$ ，函数 $f (x)$ 在 $[- 2 ， 1]$ 上的最大值与最小值互为相反数，求实数 $a$ 的值．

查看试题解析
21. 定义在 $R$ 上的函数 $f (x)$ 满足 $f (- x) + f (x) = 0$ 且 $f (x + 1) = - f (x)$ ．当 $x \in (0 ， 1)$ 时， $f (x) = \frac{3^{x}}{3^{x} + 1}$ ．

(1)、求 $f (x)$ 在 $[- 1 ， 1]$ 上的解析式；

(2)、当 $m$ 为何值时，关于 $x$ 的方程 $f (x) = 2 m$ 在区间 $[0 ， 1]$ 上有实数解．

查看试题解析
22. 已知函数 $f (x) = 4 x + 3$ ， $g (x) = x^{2} + 1$

(1)、直接写出函数 $h (x) = x g (x) - f (x)$ 的零点个数（不要求写过程）；

(2)、若 $\exists x \in R$ ，使关于 $x$ 的不等式 $m g (x) > f (x)$ 能成立，求实数 $m$ 的取值范围.

查看试题解析