河南省平顶山市2020-2021学年高一下学期数学期末考试试卷

试卷更新日期：2021-08-12 类型：期末考试

进入出卷网下载

一、单选题

1. 某电视台为了解新推出的一档综艺节目的观众认可度，从某小区的120人中，用分层抽样的方法抽取30人进行访问，已知这120人中有年轻人60人，中年人40人，老年人20人，则需要抽取的老年人的数量为（）

A、5 B、6 C、10 D、12

查看试题解析
2. 已知向量 $\vec{a} = (m ， 2 m - 1)$ ， $\vec{b} = (m + 1 ， 2)$ .若 $\vec{a}$ 与 $\vec{b}$ 同向，则 $m =$ （）

A、 $- \frac{1}{2}$ B、1 C、-1 D、 $\frac{1}{2}$

查看试题解析
3. 从800名同学中，用系统抽样（等距）的方法抽取一个20人的样本，将这800名同学按1～800进行随机编号，若抽出的第一个号码为3号，则第五个应抽的号码为（）

A、83 B、123 C、163 D、203

查看试题解析
4. $\sin \frac{8 π}{9} \sin \frac{2 π}{9} + \cos \frac{8 π}{9} \cos \frac{2 π}{9} =$ （）

A、 $\frac{\sqrt{3}}{2}$ B、 $\frac{1}{2}$ C、 $- \frac{\sqrt{3}}{2}$ D、 $- \frac{1}{2}$

查看试题解析
5. 函数 $y = 2 \cos (2 x - \frac{π}{3})$ 的图象在 $y$ 轴右侧且距 $y$ 轴最近的对称轴方程为（）

A、 $x = \frac{2 π}{3}$ B、 $x = \frac{π}{3}$ C、 $x = \frac{π}{6}$ D、 $x = \frac{π}{2}$

查看试题解析
6. 已知角 $α$ 的顶点在原点上，始边在 $x$ 轴的非负半轴上，终边经过点 $(3 ， 4)$ ，则 $\tan (α + \frac{π}{4}) =$ （）

A、7 B、 $\frac{1}{7}$ C、 $- \frac{1}{7}$ D、 $- 7$

查看试题解析
7. 设样本数据1，3， $m$ ， $n$ ，9的平均数为5，方差为8，则此样本的中位数为（）

A、3 B、4 C、5 D、6

查看试题解析
8. 某算法的程序框图如图，则输出的 $S$ 值为（）

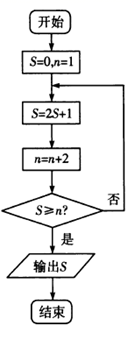A、3 B、7 C、9 D、15

查看试题解析
9. 从区间 $[0 ， 1]$ 上随机抽取 $3 n$ 个数 $x_{1} ， x_{2} ， \dots ， x_{n} ， y_{1} ， y_{2} ， \dots ， y_{n} ， z_{1} ， z_{2} ， \dots ， z_{n}$ ，成 $n$ 个数组 $(x_{1} ， y_{1} ， z_{1}) ， (x_{2} ， y_{2} ， z_{2}) ， \dots ， (x_{n} ， y_{n} ， z_{n})$ ，其中三个数的平方和小于1的数组共有 $m$ 个，则用随机模拟的方法得到的圆周率 $π$ 的近似值为（）

A、 $\frac{6 m}{n}$ B、 $\frac{3 m}{n}$ C、 $\frac{6 n}{m}$ D、 $\frac{3 n}{m}$

查看试题解析
10. 设函数 $f (x) = \sin (ω x + \frac{π}{3})$ 在 $[- \frac{π}{2} ， \frac{π}{2}]$ 上的图象大致如图，则 $f (x)$ 的最小正周期为（）

A、 $\frac{2 π}{3}$ B、 $\frac{4 π}{5}$ C、 $\frac{5 π}{6}$ D、 $\frac{8 π}{5}$

查看试题解析
11. 在 $△ A B C$ 中， $∠ C = 3 ∠ B$ ， $∠ A = 2 ∠ B$ ， $A T$ 平分 $∠ C A B$ 交 $B C$ 于点 $T$ ，若 $\vec{A T} = λ \vec{A C} + μ \vec{A B}$ ，则 $λ^{2} + μ^{2} =$ （）

A、 $\frac{4}{9}$ B、 $\frac{2}{9}$ C、 $\frac{2}{3}$ D、 $\frac{5}{9}$

查看试题解析
12. 函数 $f (x) = \tan \frac{π}{2} x$ 和 $g (x) = \frac{1}{x - 2}$ 的图象在区间 $(- 1 ， 5)$ 上交点的横坐标之和为（）

A、6 B、4 C、8 D、12

查看试题解析

二、填空题

13. 学校进行30秒跳绳测试，某小组8名同学的跳绳个数如下面的茎叶图所示，则该组数据的方差为.

查看试题解析
14. 一个不透明的口袋中装有5个小球，其中有1个红球，2个白球，2个黑球，这些小球除颜色外其他完全相同，从中随机取出2个球，则它们的颜色不相同的概率是.

查看试题解析
15. 在 $△ A B C$ 中， $A B = A C = 2$ ， $B C = 2 \sqrt{3}$ ， $P$ 为线段 $B C$ 上的一个动点，则 $\vec{A P} \cdot \vec{B P}$ 的最小值为.

查看试题解析
16. 设 $α ， β \in [0 ， π]$ ， $\sin α \cos β - \cos α \sin β = 1$ ，则 $\sin (2 α - β) + \sin (2 β - α)$ 的取值范围是.

查看试题解析

三、解答题

17. 已知向量 $\vec{a}$ 与 $\vec{b}$ 的夹角为 $60 °$ ， $| \vec{a} | = 1$ ， $| \vec{b} | = 2$ .

(1)、求 $| 3 \vec{a} + \vec{b} |$ ；

(2)、若 $(\vec{a} + λ \vec{b})$ 和 $(\vec{a} - 2 \vec{b})$ 垂直，求实数 $λ$ 的值.

查看试题解析
18. 某公司生产的一款新产品在2021年前5个月的销售情况如下表所示：

月份 $x$

1

2

3

4

5

月销售额 $y$ /万元

16

25

37

55

75

(1)、利用所给数据求月销售额 $y$ （万元）和月份 $x$ 之间的回归直线方程；

(2)、利用（1）中所求的方程预测该公司这款产品上半年的总销售额.
参考公式：回归直线方程 $\hat{y} = \hat{b} x + \hat{a}$ 中， $\hat{b} = \frac{\sum_{i = 1}^{n} x_{i} y_{i} - n \bar{x} \bar{y}}{\sum_{i = 1}^{n} x_{i}^{2} - n {\bar{x}}^{2}} ， \hat{a} = \bar{y} - \hat{b} \bar{x}$ ， $\hat{a} = \bar{y} - \hat{b} \bar{x}$ .

参考数据： $\sum_{i = 1}^{5} x_{i} y_{i} = 772$ ， $\sum_{i = 1}^{5} x_{i}^{2} = 55$ .

查看试题解析
19. 设函数 $f (x) = {(\sin x + \cos x)}^{2} + 2 \sin (π + x) \sin x$ .

(1)、求 $f (x)$ 的值域，并说明 $y = f (x)$ 的图象可由 $y = sin x$ 的图象经过怎样的变换得到；

(2)、若 $f (α) + f (- α) = \frac{\sqrt{6}}{2}$ ， $α \in (0 ， \frac{π}{4})$ ，求 $f (\frac{3 π}{8} - α)$ .

查看试题解析
20. 为庆祝中国共产党成立100周年，某校高二年级600名学生参加党史知识竞赛，根据文科生和理科生的人数比例，使用分层抽样的方法从中抽取了100名学生，将他们的分数按照 $[40 ， 50)$ ， $[50 ， 60)$ ，…， $[90 ， 100)$ ，分组，整理得到如图所示的频率分布直方图.

(1)、从该校高二学生中随机抽取1人，估计其分数小于80的概率；

(2)、已知样本中分数小于50的有4人，估计该校高二学生分数在 $[50 ， 60)$ 内的人数；

(3)、已知样本中有一半文科生的分数不小于80，且样本中分数不小于80的文科生和理科生人数相等，求该校高二年级文科生与理科生的人数之比.

查看试题解析
21. 如图所示，在梯形 $A B C D$ 中， $A B // C D$ ， $△ A B C$ 是一个边长为6的等边三角形， $M$ ， $N$ 分别是 $A C$ ， $B D$ 的中点， $A C$ 交 $B D$ 于 $O$ 点.

(1)、证明： $\vec{M N} = \frac{1}{2} (\vec{A B} + \vec{C D})$ ；

(2)、设 $\vec{D O} = 4 \vec{O N}$ ，求 $\vec{A C} \cdot \vec{B D}$ 的值.

查看试题解析
22. 已知函数 $f (x) = A \cos (ω x + φ) (A > 0 ， 1 < ω < 2 ， 0 < φ < π)$ 的图象经过点 $(0 ， 1)$ ，且一个最高点的坐标为 $(- \frac{2}{3} ， 2)$ .

(1)、求函数 $f (x)$ 的解析式：

(2)、设 $P$ ， $Q$ 分别为函数 $f (x)$ 的图象在 $y$ 轴右侧且距 $y$ 轴最近的最高点和最低点， $O$ 为坐标原点，实数 $m = \vec{O P} \cdot \vec{O Q}$ ，若函数 $g (x) = 9 m \cos 2 x + 4 n \cos x - 3$ 在 $[- \frac{π}{6} ， \frac{2 π}{3}]$ 上的最小值为-8，求实数 $n$ 的值.

查看试题解析

月份 $x$	1	2	3	4	5
月销售额 $y$ /万元	16	25	37	55	75