河南省开封市五县联考2020-2021学年高一下学期数学期末考试试卷

试卷更新日期：2021-08-12 类型：期末考试

进入出卷网下载

一、单选题

1. 已知点 $P (\tan α ， s i n α)$ 在第三象限，则角 $α$ 的终边所在的象限为（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
2. 某班学生共有56人，学号分别是 $1 ， 2 ， 3 ， ...56$ ．现用系统抽样的方法抽取一个容量为4的样本．已知学号为 $6 ， 34 ， 48$ 的同学在样本中，那么还有一名同学的学号是（）

A、19 B、20 C、24 D、44

查看试题解析
3. 某地区经过一年的新农村建设，农村的经济收入增加了一倍，实现翻番。为更好地了解该地区农村的经济收入变化情况，统计了该地区新农村建设前后农村的经济收入构成比例。得到如下饼图：

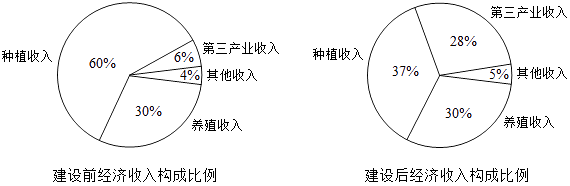
则下面结论中不正确的是（）

A、新农村建设后，种植收入减少 B、新农村建设后，其他收入增加了一倍以上 C、新农村建设后，养殖收入增加了一倍 D、新农村建设后，养殖收入与第三产业收入的总和超过了经济收入的一半

查看试题解析
4. 用更相减损术求294和84的最大公约数时，需做减法的次数是（）

A、2 B、3 C、4 D、5

查看试题解析
5. 在△ $A B C$ 中， $A D$ 为 $B C$ 边上的中线，E为 $A D$ 的中点，则 $\overset{⇀}{E B} =$ （）

A、 $\frac{3}{4} \overset{⇀}{A B} - \frac{1}{4} \overset{⇀}{A C}$ B、 $\frac{1}{4} \overset{⇀}{A B} - \frac{3}{4} \overset{⇀}{A C}$ C、 $\frac{3}{4} \overset{⇀}{A B} + \frac{1}{4} \overset{⇀}{A C}$ D、 $\frac{1}{4} \overset{⇀}{A B} + \frac{3}{4} \overset{⇀}{A C}$

查看试题解析
6. 若 $α \in (0 ， \frac{π}{2})$ ，且 $1 + \cos 2 α + 2 \sin 2 α = \frac{7}{5}$ ，则 $\tan α =$ （）

A、 $\frac{1}{7}$ B、 $\frac{1}{3}$ C、3 D、7

查看试题解析
7. 已知 $△ A B C$ 的内角 $A ， B ， C$ 所对的边分别为 $a ， b ， c ，$ 若 $\sin A + \sqrt{3} \cos A = 0 ， a = \sqrt{7} ， b = 1$ ，则 $c$ =（）

A、1 B、2 C、3 D、4

查看试题解析
8. 已知函数 $f (x) = \sin (ω x + φ) (x \in R ， ω > 0 ， | φ | < \frac{π}{2})$ 的部分图像如图所示，如果 $x_{1}$ ， $x_{2} \in (- \frac{π}{6} ， \frac{π}{3})$ ，且 $f (x_{1}) = f (x_{2})$ ，则 $f (x_{1} + x_{2}) =$ （）

A、 $\frac{1}{2}$ B、 $\frac{\sqrt{2}}{2}$ C、 $\frac{\sqrt{3}}{2}$ D、1

查看试题解析
9. 任取一个三位正整数 $n$ ，则 $\log_{2} n$ 是一个正整数的概率是（）

A、 $\frac{1}{255}$ B、 $\frac{1}{300}$ C、 $\frac{1}{450}$ D、 $\frac{1}{899}$

查看试题解析
10. 如图是求 $\frac{1}{2 + \frac{1}{2 + \frac{1}{2}}}$ 的程序框图，图中空白框中应填入（）

A、A= $\frac{1}{2 + A}$ B、A= $2 + \frac{1}{A}$ C、A= $\frac{1}{1 + 2 A}$ D、A= $1 + \frac{1}{2 A}$

查看试题解析
11. 甲、乙两艘轮船都要在某个泊位停靠6个小时，假定它们在一昼夜的时间中随机到达，这两艘轮船中至少有一艘在停靠泊位时必须等待的概率是（）

A、 $\frac{5}{16}$ B、 $\frac{11}{16}$ C、 $\frac{9}{16}$ D、 $\frac{7}{16}$

查看试题解析
12. 给出下列结论：
⑴若 $α$ 在第四象限，则 $2 α$ 角的终边在第三或第四象限；

⑵正切函数在定义域内是单调递增函数；

⑶正方体的边长与体积成正相关；

⑷抛一枚均匀的硬币4次，则出现正面的次数多于反面次数的概率为 $\frac{5}{16}$ ．

其中正确结论的个数是（）

A、0 B、1 C、2 D、3

查看试题解析

二、填空题

13. 将 $10212_{⑶}$ 转化为十进制数是．

查看试题解析
14. 与向量 $\vec{a} = (1 ， - 1)$ 共线的单位向量是．

查看试题解析
15. 已知函数 $f (x) = sin x - \sqrt{3} cos x$ ，当 $x = θ$ 时 $f (x)$ 有最大值，此时 $cos θ =$ ．

查看试题解析
16. 如图，一栋建筑物AB高（30-10 $\sqrt{3}$ ）m，在该建筑物的正东方向有一个通信塔CD．在它们之间的地面M点（B、M、D三点共线）测得对楼顶A、塔顶C的仰角分别是15°和60°，在楼顶A处测得对塔顶C的仰角为30°，则通信塔CD的高为m．

查看试题解析

三、解答题

17. △ABC的内角A，B，C的对边分别为a，b，c，已知2cosC（acosB+bcosA）=c．

(1)、求C；

(2)、若 $c = \sqrt{7}, △ A B C$ 的面积为 $\frac{3 \sqrt{3}}{2}$ ，求△ABC的周长．

查看试题解析
18. 某大学艺术专业400名学生参加某次测评，根据男女学生人数比例，使用分层抽样的方法从中随机抽取了100名学生，记录他们的分数，将数据分成7组： $[20 ， 30)$ 、…、 $[80 ， 90]$ ，并整理得到如图所示的频率分布直方图.

(1)、从总体的400名学生中随机抽取一人，估计其分数小于70的概率；

(2)、已知样本中分数小于40的学生有5人，试估计总体中分数在区间 $[40 ， 50)$ 内的人数；

(3)、已知样本中有一半男生的分数不小于70，且样本中分数不小于70的男女生人数相等.试估计总体中男生和女生人数的比例.

查看试题解析
19. 已知向量 $\vec{a} = (\sqrt{3} ， - 1) ， \vec{b} = (\frac{1}{2} ， \frac{\sqrt{3}}{2})$ ．

(1)、求证： $\vec{a} ⊥ \vec{b}$ ；

(2)、是否存在不等于 $0$ 的实数 $k$ 和 $t$ ，使 $\vec{x} = \vec{a} + (t^{2} - 3) \vec{b} ， \vec{y} = - k \vec{a} + t \vec{b}$ ，且 $\vec{x} ⊥ \vec{y}$ ？如果存在，试写出 $k = f (t)$ 的关系式；如果不存在，请说明理由．．

查看试题解析
20. 已知函数 $f (x) = \sqrt{3} \cos^{2} \frac{ω x}{2} + \sin \frac{ω x}{2} \cos \frac{ω x}{2} (ω > 0)$ 的最小正周期是 $2 π$ ．

(1)、求 $f (\frac{5 π}{6})$ 的值；

(2)、若 $- \frac{π}{3} < α < \frac{π}{6}$ ，且 $f (α) = \frac{3}{5} + \frac{\sqrt{3}}{2}$ ，求 $\cos (2 α + \frac{π}{6})$ ．

查看试题解析
21. 某企业为了参加上海的进博会，大力研发新产品，为了对新研发的一批产品进行合理定价，将该产品按事先拟定的价格进行试销，得到一组销售数据（ $x_{i}$ ， $y_{i}$ ）（ $i = 1 ， 2 ， \dots ， 6$ ），如表所示：

试销单价 $x$ /元

4

5

6

7

8

9

产品销量 $y$ /件

$q$

84

83

80

75

68

已知 $\bar{y} = \frac{1}{6} \sum_{i = 1}^{6} y_{i} = 80$ ．

(1)、求 $q$ 的值；

(2)、已知变量 $x$ ， $y$ 具有线性相关关系，求产品销量 $y$ （件）关于试销单价 $x$ （元）的线性回归方程 $\hat{y} = \hat{b} x + \hat{a}$ ；

(3)、用 ${\hat{y}}_{i}$ 表示用正确的线性回归方程得到的与 $x_{i}$ 对应的产品销量的估计值，当 $| {\hat{y}}_{i} - y_{i} | \leq 1$ 时，将销售数据（ $x_{i}$ ， $y_{i}$ ）称为一个“好数据”，现从6个销售数据中任取2个，求抽取的2个销售数据中至少有一个是“好数据”的概率．
参考公式： $\hat{b} = \frac{\sum_{i = 1}^{n} x_{i} y_{i} - n \bar{x} \bar{y}}{\sum_{i = 1}^{n} x_{i}^{2} - n {\bar{x}}^{2}} = \frac{\sum_{i = 1}^{n} (x_{i} - \bar{x}) (y_{i} - \bar{y})}{\sum_{i = 1}^{n} {(x_{i} - \bar{x})}^{2}}$ ， $\hat{a} = \bar{y} - \hat{b} x$ ．

查看试题解析
22. 某学校的平面示意图为如下图五边形区域 $A B C D E$ ，其中三角形区域 $A B E$ 为生活区，四边形区域 $B C D E$ 为教学区， $A B ， B C ， C D ， D E ， E A ， B E$ 为学校的主要道路（不考虑宽度）. $D E = 3 B C = 3 C D = \frac{9}{10} k m$ ， $∠ B C D = ∠ C D E = \frac{2 π}{3} ， ∠ B A E = \frac{π}{3}$ .

(1)、求道路 $B E$ 的长度；

(2)、求生活区 $Δ A B E$ 面积的最大值.

查看试题解析

试销单价 $x$ /元	4	5	6	7	8	9
产品销量 $y$ /件	$q$	84	83	80	75	68