河北省唐山市2020-2021学年高一下学期数学期末考试试卷

试卷更新日期：2021-08-12 类型：期末考试

进入出卷网下载

一、单选题

1. 设复数 $z = - i + 2$ ，则 $z$ 的虚部为（）

A、2 B、-1 C、 $i$ D、 $- i$

查看试题解析
2. 已知向量 $\vec{a} = (- 4 ， 3)$ ， $\vec{a} + 3 \vec{b} = (5 ， - 3)$ ，则 $\vec{b} =$ （）

A、 $(- 3 ， 2)$ B、 $(3 ， - 2)$ C、 $(3 ， 0)$ D、 $(9 ， 6)$

查看试题解析
3. 某小区约有3000人，需对小区居民身体状况进行分层抽样调查，样本中有幼龄12人，青壮龄34人，老龄14人，则该小区老龄人数的估计值为（）

A、750 B、1700 C、600 D、700

查看试题解析
4. 为了了解某道口堵车情况，在今后的三天中，假设每一天堵车的概率均为40%．现采用模拟试验的方法估计这三天中恰有两天堵车的概率：先利用计算器产生0到9之间的随机整数，用1、2、3、4表示堵车，用5、6、7、8、9、0表示不堵车：再以每三个数作为一组，代表这三天的堵车情况．经试验产生了如下20组随机数：
$\begin{matrix} 807 & 066 & 123 & 923 & 471 & 532 & 712 & 259 & 507 & 752 \\ 443 & 277 & 303 & 927 & 756 & 368 & 840 & 413 & 730 & 086 \end{matrix}$

据此估计，这三天中恰有两天堵车的概率近似为（）

A、0.25 B、0.3 C、0.35 D、0.40

查看试题解析
5. 如图，直角梯形 $O A B C$ 的上、下两底分别为1和2，高为 $\sqrt{2}$ ，则利用斜二测画法所得其直观图的面积为（）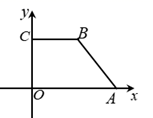

A、 $\frac{1}{2}$ B、 $\frac{3}{4}$ C、 $\frac{3 \sqrt{2}}{8}$ D、 $\frac{3 \sqrt{2}}{4}$

查看试题解析
6. 同时投掷两个质地均匀的骰子，两个骰子的点数至少有一个是奇数的概率为（）

A、 $\frac{7}{36}$ B、 $\frac{11}{36}$ C、 $\frac{11}{12}$ D、 $\frac{3}{4}$

查看试题解析
7. 如图，四边形ABCD是正方形，延长CD至E ，使得DE＝CD ，若点P为CD的中点，且 $\vec{A P} = λ \vec{A B} + μ \vec{A E}$ ，则 $λ + μ =$ （）

A、3 B、 $\frac{5}{2}$ C、2 D、1

查看试题解析
8. 在 $△ A B C$ 中，角 $A$ ， $B$ ， $C$ 所对的边分别为 $a$ ， $b$ ， $c$ ， $A = 150 °$ ， $D$ 是边 $B C$ 上一点， $A B ⊥ A D$ ，且 $A D = 1$ ，则 $b + \sqrt{3} c$ 的最小值为（）

A、 $5 + 2 \sqrt{6}$ B、12 C、 $5 + 2 \sqrt{3}$ D、20

查看试题解析

二、多选题

9. 已知两条直线 $m$ ， $n$ ，两个平面 $α$ ， $β$ ．下列说法正确的是（）

A、若 $m / / n$ ， $m ⊥ α$ ，则 $n ⊥ α$ B、若 $α / / β$ ， $m \subset α$ ， $n \subset β$ ，则 $m / / n$ C、若 $m / / n$ ， $m / / α$ ，则 $n / / α$ D、若 $α / / β$ ， $m / / n$ ， $m ⊥ α$ ，则 $n ⊥ β$

查看试题解析
10. 在 $△ A B C$ 中， $\sin^{2} B \leq \sin^{2} A + \sin^{2} C - \sin A \sin C$ ，则 $B$ 可以是（）

A、 $\frac{π}{6}$ B、 $\frac{π}{3}$ C、 $\frac{π}{2}$ D、 $\frac{2 π}{3}$

查看试题解析
11. 一个口袋内装有大小、形状相同的红色、绿色和蓝色小球各2个，一次任意取出2个小球，则与事件“2个小球都为红色”互斥而不对立的事件有（）

A、2个小球不全为红球 B、2个小球恰有1个红球 C、2个小球至少有1个红球 D、2个小球都为绿球

查看试题解析
12. 如图，已知平行四边形 $A B C D$ 中， $∠ A B C = 60 °$ ， $A D = 2 A B$ ， $M$ 为边 $B C$ 的中点，将 $△ A B M$ 沿直线 $A M$ 翻折成 $△ A B_{1} M$ ，若 $N$ 为是 $B_{1} D$ 的中点，则在 $△ A B M$ 的翻折过程中，下列命题正确的是（）

A、线段 $C N$ 的长为定值 B、异面直线 $A M$ 与 $B_{1} D$ 所成角为 $90 °$ C、直线 $C N$ 与平面 $A B_{1} M$ 所成角为定值 D、二面角 $A - B_{1} M - D$ 可以为直二面角

查看试题解析

三、填空题

13. 已知复数 $z$ 满足 $z (1 - i) = | 1 + \sqrt{3} i |$ ，则 $z =$ ．

查看试题解析
14. 在 $△ A B C$ 中， $a = 1$ ， $b = \sqrt{3}$ ， $A = \frac{π}{6}$ ，则 $B =$ ．

查看试题解析
15. 甲、乙两人进行羽毛球单打比赛，根据以往比赛的胜负情况知道，每一局甲获胜的概率为 $\frac{2}{3}$ ，乙获胜的概率为 $\frac{1}{3}$ ，如果比赛采用“三局二胜”制（先胜二局者获胜），则前两局打平且甲获胜的概率为．

查看试题解析
16. 已知圆锥底面半径为1，母线长为3，该圆锥内接正方体的体积为．

查看试题解析

四、解答题

17. 已知向量 $\vec{a} = (- 1 ， 2)$ ， $\vec{b} = (3 ， 4)$ ．

(1)、若 $\vec{a} - \vec{b}$ 与 $2 \vec{a} + k \vec{b}$ 平行，求实数 $k$ 的值；

(2)、若 $λ \vec{a} - \vec{b}$ 与 $\vec{a} + 2 \vec{b}$ 垂直，求实数 $λ$ 的值．

查看试题解析
18. 某学校6月份定为安全教育宣传月，6月底进行安全教育测试，试卷满分为120分，随机抽取了100名学生的试卷进行研究，得到成绩的范围是 $[60 ， 120]$ （单位：分），根据统计数据得到如下频率分布直方图：

(1)、求 $m$ 的值；

(2)、估计该校安全教育测试成绩的中位数（精确到小数点后两位）；

(3)、若成绩在 $[90 ， 100)$ 赋给1颗星， $[100 ， 110)$ 赋给2颗星， $[110 ， 120]$ 赋给3颗星，将频率视作概率，若甲乙两位同学参赛且相互不影响，求两个一共得4颗星的概率．

查看试题解析
19. $△ A B C$ 中，内角 $A$ ， $B$ ， $C$ 所对的边分别为 $a$ ， $b$ ， $c$ ，已知 $a = b \cos C + \sqrt{3} a \sin (A + C)$ ， $\frac{c}{a} = 3$ ．

(1)、求角 $B$ ；

(2)、若 $△ A B C$ 的面积为 $7 \sqrt{3}$ ，求 $b$ 的值．

查看试题解析
20. 在长方体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 中，底面 $A B C D$ 是边长为2的正方形．

(1)、若 $M$ 为 $C C_{1}$ 的中点，试在 $C_{1} D_{1}$ 上确定一点 $N$ ，使得 $A_{1} B / /$ 平面 $B_{1} M N$ ；

(2)、直线 $A_{1} B$ 与平面 $A_{1} D C B_{1}$ 所成的角为 $30 °$ ，求四棱锥 $B - A_{1} D C B_{1}$ 的体积．

查看试题解析
21. 某研究所对两块试验田水稻的株高进行调研，采用样本量比例分配的分层随机抽样，如果不知道样本数据，只知道第一块试验田抽取了水稻 80株，其平均数和方差分别为107（单位：cm）和5.22，另一块试验田抽取了水稻120株，其平均数和方差分别为112（单位：cm）和30.97，你能由这些数据计算出总样本的方差，并对这种水稻的方差作出估计吗？

查看试题解析
22. 在四棱锥 $S - A B C D$ 中，侧面 $S A B ⊥$ 底面 $A B C D$ ，底面 $A B C D$ 为矩形， $△ S A B$ 为等边三角形， $A B = 1$ ， $B C = \sqrt{3}$ ，点 $E$ 在 $A D$ 上， $A E = 5 D E$ ．

(1)、求证： $C E ⊥ S D$ ；

(2)、求二面角 $E - S B - A$ 的正切值．

查看试题解析