山东省威海市2021年中考数学试卷
试卷更新日期:2021-08-12 类型:中考真卷
一、单选题
-
1. ﹣ 的相反数是( )A、﹣5 B、5 C、﹣ D、2. 据光明日报网,中国科学技术大学的潘建伟、陆朝阳等人构建了一台76个光子100个模式的量子计算机“九章”.它处理“高斯玻色取样”的速度比目前最快的超级计算机“富岳”快一百万亿倍.也就是说,超级计算机需要一亿年完成的任务,“九章”只需一分钟.其中一百万亿用科学记数法表示为( )A、 B、 C、 D、3. 若用我们数学课本上采用的科学计算器计算sin36 18',按键顺序正确的是( )A、
 B、
B、 C、
C、 D、
D、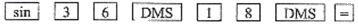 4. 下列运算正确的是( )A、 B、 C、 D、5. 如图所示的几何体是由5个大小相同的小正方体搭成的.其左视图是( )
4. 下列运算正确的是( )A、 B、 C、 D、5. 如图所示的几何体是由5个大小相同的小正方体搭成的.其左视图是( ) A、
A、 B、
B、 C、
C、 D、
D、 6. 某校为了解学生的睡眠情况,随机调查部分学生一周平均每天的睡时间,统计结果如表:
6. 某校为了解学生的睡眠情况,随机调查部分学生一周平均每天的睡时间,统计结果如表:时间/小时
7
8
9
10
人数
6
9
11
4
这些学生睡眠时间的众数、中位数是( )
A、众数是11,中位数是8.5 B、众数是9,中位数是8.5 C、众数是9,中位数是9 D、众数是10,中位数是97. 解不等式组 时,不等式①②的解集在同一条数轴上表示正确的是( )A、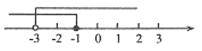 B、
B、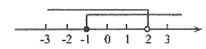 C、
C、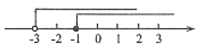 D、
D、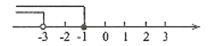 8. 在一个不透明的袋子里装有5个小球,每个球上都写有一个数字,分别是1,2,3,4,5,这些小球除数字不同外其它均相同.从中随机一次摸出两个小球,小球上的数字都是奇数的概率为( )A、 B、 C、 D、9. 如图,在平行四边形 中, , .连接AC , 过点B作 ,交DC的延长线于点E , 连接AE , 交BC于点F . 若 ,则四边形ABEC的面积为( )
8. 在一个不透明的袋子里装有5个小球,每个球上都写有一个数字,分别是1,2,3,4,5,这些小球除数字不同外其它均相同.从中随机一次摸出两个小球,小球上的数字都是奇数的概率为( )A、 B、 C、 D、9. 如图,在平行四边形 中, , .连接AC , 过点B作 ,交DC的延长线于点E , 连接AE , 交BC于点F . 若 ,则四边形ABEC的面积为( )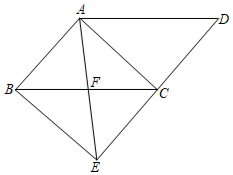 A、 B、 C、6 D、10. 一次函数 与反比例函数 的图象交于点 ,点 .当 时,x的取值范围是( )A、 B、 或 C、 D、 或11. 如图,在 和 中, , , .连接CD , 连接BE并延长交AC , AD于点F , G . 若BE恰好平分 ,则下列结论错误的是( )
A、 B、 C、6 D、10. 一次函数 与反比例函数 的图象交于点 ,点 .当 时,x的取值范围是( )A、 B、 或 C、 D、 或11. 如图,在 和 中, , , .连接CD , 连接BE并延长交AC , AD于点F , G . 若BE恰好平分 ,则下列结论错误的是( )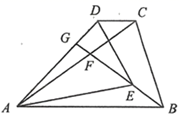 A、 B、 C、 D、12. 如图,在菱形ABCD中, , ,点P , Q同时从点A出发,点P以1cm/s的速度沿A﹣C﹣D的方向运动,点Q以2cm/s的速度沿A﹣B﹣C﹣D的方向运动,当其中一点到达D点时,两点停止运动.设运动时间为x(s), 的面积为y(cm2),则下列图象中能大致反映y与x之间函数关系的是( )
A、 B、 C、 D、12. 如图,在菱形ABCD中, , ,点P , Q同时从点A出发,点P以1cm/s的速度沿A﹣C﹣D的方向运动,点Q以2cm/s的速度沿A﹣B﹣C﹣D的方向运动,当其中一点到达D点时,两点停止运动.设运动时间为x(s), 的面积为y(cm2),则下列图象中能大致反映y与x之间函数关系的是( )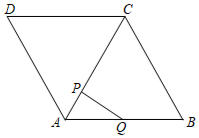 A、
A、 B、
B、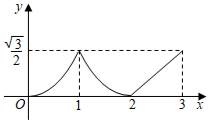 C、
C、 D、
D、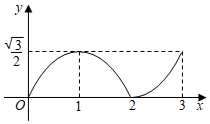
二、填空题
-
13. 计算 的结果是 .14. 分解因式: .15. 如图,在 中, ,分别以点A , B为圆心,以大于 长为半径画弧,两弧交于点D , E . 作直线DE , 交BC于点M . 分别以点A , C为圆心,以大于 长为半径画弧,两弧交于点F , G . 作直线FG , 交BC于点N . 连接AM , AN . 若 ,则 .
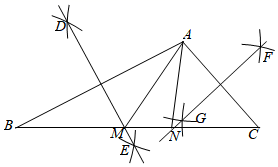 16. 已知点A为直线y=-2x上一点,过点A作 轴,交双曲线 于点B . 若点A与点B关于y轴对称,则点A的坐标为 .17. 如图,先将矩形纸片ABCD沿EF折叠(AB边与DE在CF的异侧),AE交CF于点G;再将纸片折叠,使CG与AE在同一条直线上,折痕为GH . 若 ,纸片宽 ,则HE=cm.
16. 已知点A为直线y=-2x上一点,过点A作 轴,交双曲线 于点B . 若点A与点B关于y轴对称,则点A的坐标为 .17. 如图,先将矩形纸片ABCD沿EF折叠(AB边与DE在CF的异侧),AE交CF于点G;再将纸片折叠,使CG与AE在同一条直线上,折痕为GH . 若 ,纸片宽 ,则HE=cm. 18. 如图,在正方形ABCD中, ,E为边AB上一点,F为边BC上一点.连接DE和AF交于点G , 连接BG . 若 ,则BG的最小值为 .
18. 如图,在正方形ABCD中, ,E为边AB上一点,F为边BC上一点.连接DE和AF交于点G , 连接BG . 若 ,则BG的最小值为 .
三、解答题
-
19. 先化简 ,然后从 ,0,1,3中选一个合适的数作为a的值代入求值.20. 某校为提高学生的综合素养,准备开展摄影、书法、绘画、表演、手工五类社团活动.为了对此项活动进行统筹安排,随机抽取了部分学生进行调查,要求每人从五个类别中只选择一个,将调查结果绘制成了两幅统计图(未完成).请根据统计图中的信息,解答下列问题:
 (1)、本次共调查了名学生;(2)、请将条形统计图补充完整;(3)、扇形统计图中,“摄影”所占的百分比为;“手工”所对应的圆心角的度数为 .(4)、若该校共有2700名学生,请估计选择“绘画”的学生人数.21. 六一儿童节来临之际,某商店用3000元购进一批玩具,很快售完;第二次购进时,每件的进价提高了20%,同样用3000元购进的数量比第一次少了10件.(1)、求第一次每件的进价为多少元?(2)、若两次购进的玩具售价均为70元,且全部售完,求两次的总利润为多少元?22. 在一次测量物体高度的数学实践活动中,小明从一条笔直公路上选择三盏高度相同的路灯进行测量.如图,他先在点B处安置测倾器,于点A处测得路灯MN顶端的仰角为 ,再沿BN方向前进10米,到达点D处,于点C处测得路灯PQ顶端的仰角为 .若测倾器的高度为1.2米,每相邻两根灯柱之间的距离相等,求路灯的高度(结果精确到0.1米).
(1)、本次共调查了名学生;(2)、请将条形统计图补充完整;(3)、扇形统计图中,“摄影”所占的百分比为;“手工”所对应的圆心角的度数为 .(4)、若该校共有2700名学生,请估计选择“绘画”的学生人数.21. 六一儿童节来临之际,某商店用3000元购进一批玩具,很快售完;第二次购进时,每件的进价提高了20%,同样用3000元购进的数量比第一次少了10件.(1)、求第一次每件的进价为多少元?(2)、若两次购进的玩具售价均为70元,且全部售完,求两次的总利润为多少元?22. 在一次测量物体高度的数学实践活动中,小明从一条笔直公路上选择三盏高度相同的路灯进行测量.如图,他先在点B处安置测倾器,于点A处测得路灯MN顶端的仰角为 ,再沿BN方向前进10米,到达点D处,于点C处测得路灯PQ顶端的仰角为 .若测倾器的高度为1.2米,每相邻两根灯柱之间的距离相等,求路灯的高度(结果精确到0.1米).(参考数据: , , , , , )
 23. 如图,AB是 直径,弦 ,垂足为点E . 弦BF交CD于点G , 点P在CD延长线上,且 .
23. 如图,AB是 直径,弦 ,垂足为点E . 弦BF交CD于点G , 点P在CD延长线上,且 .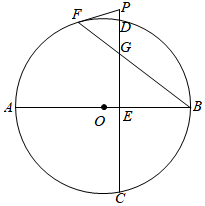 (1)、求证:PF为 切线;(2)、若 , , ,求PF的长.
(1)、求证:PF为 切线;(2)、若 , , ,求PF的长.
