辽宁省阜新市2021年中考数学试卷
试卷更新日期:2021-08-12 类型:中考真卷
一、单选题
-
1. 计算: ,其结果等于( )A、2 B、-2 C、4 D、-42. 一个几何体如图所示,它的左视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、 3. 在庆祝中国共产党成立100周年的“红色记忆”校园歌咏比赛中,15个参赛班级按照成绩(成绩各不相同)取前7名进入决赛,小红知道了自己班级的比赛成绩,如果要判断自己的班级能否进入决赛,还需要知道这15个参赛班级成绩的( )A、平均数 B、中位数 C、众数 D、方差4. 不等式组 的解集,在数轴上表示正确的是( )A、
3. 在庆祝中国共产党成立100周年的“红色记忆”校园歌咏比赛中,15个参赛班级按照成绩(成绩各不相同)取前7名进入决赛,小红知道了自己班级的比赛成绩,如果要判断自己的班级能否进入决赛,还需要知道这15个参赛班级成绩的( )A、平均数 B、中位数 C、众数 D、方差4. 不等式组 的解集,在数轴上表示正确的是( )A、 B、
B、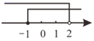 C、
C、 D、
D、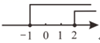 5. 已知点 , 都在反比例函数 的图象上,且 ,则 , 的关系是( )A、 B、 C、 D、6. 小颖有两顶帽子,分别为红色和黑色,有三条围巾,分别为红色、黑色和白色,她随机拿出一顶帽子和一条围巾戴上,恰好为红色帽子和红色围巾的概率是( )A、 B、 C、 D、7. 如图,A , B , C是⊙O上的三点,若 ,则 的度数是( )
5. 已知点 , 都在反比例函数 的图象上,且 ,则 , 的关系是( )A、 B、 C、 D、6. 小颖有两顶帽子,分别为红色和黑色,有三条围巾,分别为红色、黑色和白色,她随机拿出一顶帽子和一条围巾戴上,恰好为红色帽子和红色围巾的概率是( )A、 B、 C、 D、7. 如图,A , B , C是⊙O上的三点,若 ,则 的度数是( ) A、40° B、35° C、30° D、25°8. 在育红学校开展的课外阅读活动中,学生人均阅读量从七年级的每年100万字增加到九年级的每年121万字.设该校七至九年级人均阅读量年均增长率为x , 根据题意,所列方程正确的是( )A、 B、 C、 D、9. 如图,二次函数 的图象与x轴交于A , 两点,则下列说法正确的是( )
A、40° B、35° C、30° D、25°8. 在育红学校开展的课外阅读活动中,学生人均阅读量从七年级的每年100万字增加到九年级的每年121万字.设该校七至九年级人均阅读量年均增长率为x , 根据题意,所列方程正确的是( )A、 B、 C、 D、9. 如图,二次函数 的图象与x轴交于A , 两点,则下列说法正确的是( ) A、 B、点A的坐标为 C、当 时,y随x的增大而减小 D、图象的对称轴为直线10. 如图,弧长为半圆的弓形在坐标系中,圆心在 .将弓形沿x轴正方向无滑动滚动,当圆心经过的路径长为 时,圆心的横坐标是( )
A、 B、点A的坐标为 C、当 时,y随x的增大而减小 D、图象的对称轴为直线10. 如图,弧长为半圆的弓形在坐标系中,圆心在 .将弓形沿x轴正方向无滑动滚动,当圆心经过的路径长为 时,圆心的横坐标是( )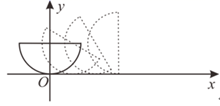 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
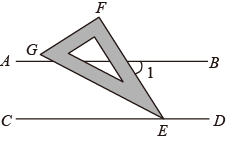
11. 计算: .12. 如图,直线 ,一块含有30°角的直角三角尺顶点E位于直线CD上,EG平分 ,则 的度数为°.
 13. 如图,已知每个小方格的边长均为1,则 与 的周长比为 .
13. 如图,已知每个小方格的边长均为1,则 与 的周长比为 .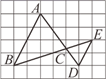 14. 如图,甲楼高21m,由甲楼顶看乙楼顶的仰角是45°,看乙楼底的俯角是30°,则乙楼高度约为 m(结果精确到1m, ).
14. 如图,甲楼高21m,由甲楼顶看乙楼顶的仰角是45°,看乙楼底的俯角是30°,则乙楼高度约为 m(结果精确到1m, ).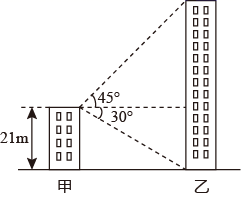 15. 如图,折叠矩形纸片ABCD , 使点B的对应点E落在CD边上,GH为折痕,已知 , .当折痕GH最长时,线段BH的长为 .
15. 如图,折叠矩形纸片ABCD , 使点B的对应点E落在CD边上,GH为折痕,已知 , .当折痕GH最长时,线段BH的长为 .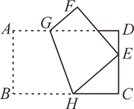 16. 育红学校七年级学生步行到郊外旅行.七(1)班出发1h后,七(2)班才出发,同时七(2)班派一名联络员骑自行车在两班队伍之间进行联络,联络员和七(1)班的距离s(km)与七(2)班行进时间t(h)的函数关系图象如图所示.若已知联络员用了 第一次返回到自己班级,则七(2)班需要 h才能追上七(1)班.
16. 育红学校七年级学生步行到郊外旅行.七(1)班出发1h后,七(2)班才出发,同时七(2)班派一名联络员骑自行车在两班队伍之间进行联络,联络员和七(1)班的距离s(km)与七(2)班行进时间t(h)的函数关系图象如图所示.若已知联络员用了 第一次返回到自己班级,则七(2)班需要 h才能追上七(1)班.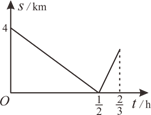
三、解答题
-
17. 先化简,再求值: ,其中 .18. 下面是小明关于“对称与旋转的关系”的探究过程,请你补充完整.
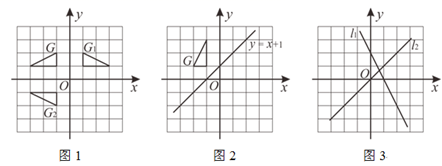 (1)、三角形在平面直角坐标系中的位置如图1所示,简称G , G关于y轴的对称图形为 ,关于 轴的对称图形为 .则将图形 绕点顺时针旋转度,可以得到图形 .(2)、在图2中分别画出G关于y轴和直线 的对称图形 , . 将图形 绕 点(用坐标表示)顺时针旋转 度,可以得到图形 .(3)、综上,如图3,直线 和 所夹锐角为 ,如果图形G关于直线 的对称图形为 ,关于直线 的对称图形为 ,那么将图形 绕点(用坐标表示)顺时针旋转度(用 表示),可以得到图形 .19. 育红学校为了了解学生家长对教育部《关于进一步加强中小学生睡眠管理工作的通知》(以下简称《通知》)的了解程度,随机抽取了该校部分学生家长进行问卷调查,问卷分为A(十分了解),B(了解较多),C(了解较少),D(不了解)四个选项,要求每位被调查家长必选且只能选择其中的一项.在对调查数据进行统计分析时,绘制了如图所示的两幅不完整的统计图,请你依据图中信息解答下列问题:
(1)、三角形在平面直角坐标系中的位置如图1所示,简称G , G关于y轴的对称图形为 ,关于 轴的对称图形为 .则将图形 绕点顺时针旋转度,可以得到图形 .(2)、在图2中分别画出G关于y轴和直线 的对称图形 , . 将图形 绕 点(用坐标表示)顺时针旋转 度,可以得到图形 .(3)、综上,如图3,直线 和 所夹锐角为 ,如果图形G关于直线 的对称图形为 ,关于直线 的对称图形为 ,那么将图形 绕点(用坐标表示)顺时针旋转度(用 表示),可以得到图形 .19. 育红学校为了了解学生家长对教育部《关于进一步加强中小学生睡眠管理工作的通知》(以下简称《通知》)的了解程度,随机抽取了该校部分学生家长进行问卷调查,问卷分为A(十分了解),B(了解较多),C(了解较少),D(不了解)四个选项,要求每位被调查家长必选且只能选择其中的一项.在对调查数据进行统计分析时,绘制了如图所示的两幅不完整的统计图,请你依据图中信息解答下列问题: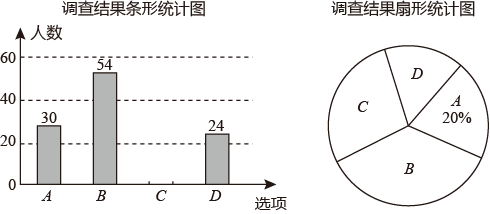 (1)、参与这次学校调查的学生家长共人;(2)、通过计算将条形统计图补充完整;(3)、若该校共有2000名学生家长,请估计该校学生家长中对《通知》“十分了解”和“了解较多”的一共约有多少人?20. 为落实“数字中国”的建设工作,市政府计划对全市中小学多媒体教室进行安装改造,现安排两个安装公司共同完成.已知甲公司安装工效是乙公司安装工效的1.5倍,乙公司安装36间教室比甲公司安装同样数量的教室多用3天.(1)、求甲、乙两个公司每天各安装多少间教室?(2)、已知甲公司安装费每天1000元,乙公司安装费每天500元,现需安装教室120间,若想尽快完成安装工作且安装总费用不超过18000元,则最多安排甲公司工作多少天?21. 在图1中似乎包含了一些曲线,其实它们是由多条线段构成的.它不但漂亮,还蕴含着很多美妙的数学结论.如图,在正方形ABCD中,E , F分别是直线AB , BC上的点(E , F在直线AC的两侧),且 .
(1)、参与这次学校调查的学生家长共人;(2)、通过计算将条形统计图补充完整;(3)、若该校共有2000名学生家长,请估计该校学生家长中对《通知》“十分了解”和“了解较多”的一共约有多少人?20. 为落实“数字中国”的建设工作,市政府计划对全市中小学多媒体教室进行安装改造,现安排两个安装公司共同完成.已知甲公司安装工效是乙公司安装工效的1.5倍,乙公司安装36间教室比甲公司安装同样数量的教室多用3天.(1)、求甲、乙两个公司每天各安装多少间教室?(2)、已知甲公司安装费每天1000元,乙公司安装费每天500元,现需安装教室120间,若想尽快完成安装工作且安装总费用不超过18000元,则最多安排甲公司工作多少天?21. 在图1中似乎包含了一些曲线,其实它们是由多条线段构成的.它不但漂亮,还蕴含着很多美妙的数学结论.如图,在正方形ABCD中,E , F分别是直线AB , BC上的点(E , F在直线AC的两侧),且 .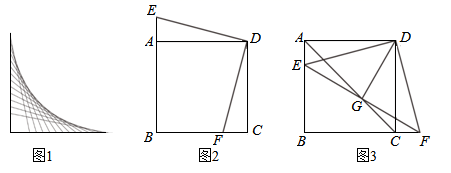 (1)、如图2,求证: ;(2)、若直线AC与EF相交于点G , 如图3,求证: ;(3)、设正方形ABCD的中心为O , ,用含 的式子表示 的度数(不必证明).22. 在平面直角坐标系中,抛物线 交x轴于点 , ,过点B的直线 交抛物线于点C.
(1)、如图2,求证: ;(2)、若直线AC与EF相交于点G , 如图3,求证: ;(3)、设正方形ABCD的中心为O , ,用含 的式子表示 的度数(不必证明).22. 在平面直角坐标系中,抛物线 交x轴于点 , ,过点B的直线 交抛物线于点C. (1)、求该抛物线的函数表达式;(2)、若点P是直线BC下方抛物线上的一个动点(P不与点B , C重合),求 面积的最大值;(3)、若点M在抛物线上,将线段OM绕点O旋转90°,得到线段ON , 是否存在点M , 使点N恰好落在直线BC上?若存在,请直接写出点M的坐标;若不存在,请说明理由.
(1)、求该抛物线的函数表达式;(2)、若点P是直线BC下方抛物线上的一个动点(P不与点B , C重合),求 面积的最大值;(3)、若点M在抛物线上,将线段OM绕点O旋转90°,得到线段ON , 是否存在点M , 使点N恰好落在直线BC上?若存在,请直接写出点M的坐标;若不存在,请说明理由.