初中数学浙教版八年级上册3.4 一元一次不等式组同步练习
试卷更新日期:2021-08-11 类型:同步测试
一、单选题
-
1. 不等式组 的解集为( )A、 B、 C、 D、无解2. 若关于x的不等式组 恰有3个整数解,则实数a的取值范围是( )A、 B、 C、 D、3. 不等式1<2x-3<x+1的解集是( )A、1<x<2 B、2<x<3 C、2<x<4 D、4<x<54. 不等式组 的解集在以下数轴表示中正确的是( )A、
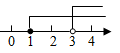 B、
B、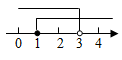 C、
C、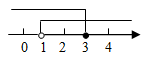 D、
D、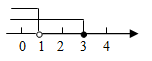 5. 若数m使关于x的一元一次不等式组 的解集是 ,且使关于y的分式方程 有非负整数解,则符合条件的所有整数m的值之和为( )A、-3 B、0 C、2 D、56. 对一个实数x按如图所示的程序进行操作,规定:程序运行从“输入一个实数x”到“判断结果是否大于190?”为一次操作,如果操作恰好进行两次就停止了,那么x的取值范围是( )
5. 若数m使关于x的一元一次不等式组 的解集是 ,且使关于y的分式方程 有非负整数解,则符合条件的所有整数m的值之和为( )A、-3 B、0 C、2 D、56. 对一个实数x按如图所示的程序进行操作,规定:程序运行从“输入一个实数x”到“判断结果是否大于190?”为一次操作,如果操作恰好进行两次就停止了,那么x的取值范围是( ) A、8<x≤22 B、8≤x<22 C、8<x≤64 D、22<x≤647. 不等式组 的整数解的和为( )A、1 B、0 C、-1 D、-28. 不等式组 的最小整数解是( )A、-2 B、-1 C、0 D、59. 不等式组 的整数解的个数为( )A、2 B、3 C、4 D、510. 不等式组 的最大整数解是( )A、-3 B、-2 C、-1 D、0
A、8<x≤22 B、8≤x<22 C、8<x≤64 D、22<x≤647. 不等式组 的整数解的和为( )A、1 B、0 C、-1 D、-28. 不等式组 的最小整数解是( )A、-2 B、-1 C、0 D、59. 不等式组 的整数解的个数为( )A、2 B、3 C、4 D、510. 不等式组 的最大整数解是( )A、-3 B、-2 C、-1 D、0二、填空题
-
11. 如果关于x的不等式组 恰有2个整数解,则a的取值范围是.12. 不等式组 的解集是.13. 不等式 的正整数解为.14. 若关于x的一元一次不等式组 仅有2个整数解,则m的取值范围是.15. 对一个实数x 按如图所示的程序进行操作,规定:程序运行从“输入一个实数x”到“结果是否大于88?"为一次操作.如果操作进行了两次就停止,则x的取值范围是
 16. 已知关于x的不等式组 的整数解只有3个,则m的取值范围是
16. 已知关于x的不等式组 的整数解只有3个,则m的取值范围是三、解答题
-
17. 解不等式组: ,并在数轴上表示它的解集.
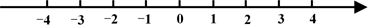 18. 取哪些正整数值时,不等式 与 都成立?19. 解一元一次不等式组,并把它的解集在数轴上表示出来 .
18. 取哪些正整数值时,不等式 与 都成立?19. 解一元一次不等式组,并把它的解集在数轴上表示出来 . 20. 解不等式组 ,并求出它的所有整数解的和.21. 解不等式组 .22. 解不等式组 并写出不等式组的非负整数解.
20. 解不等式组 ,并求出它的所有整数解的和.21. 解不等式组 .22. 解不等式组 并写出不等式组的非负整数解.