初中数学浙教版八年级上册3.2 不等式的基本性质同步练习

试卷更新日期：2021-08-11 类型：同步测试

进入出卷网下载

一、单选题

1. 若a＞b，则下列不等式不成立的是（）

A、a＋3＞b＋3 B、3a＞3b C、 $\frac{a}{3} > \frac{b}{3}$ D、－3a＞－3b

查看试题解析
2. 已知 $a > b$ ，则下列不等式一定成立的是（）

A、 $a - 1 < b - 1$ B、 $2 a < 2 b$ C、 $- 2 a < - 2 b$ D、 $a + 2 < b + 2$

查看试题解析
3. 下列说法错误的是（）

A、若 $a > b$ ，则 $a + 3 > b + 3$ B、若 $a > b$ ，则 $a c^{2} > b c^{2}$ C、若 $a c^{2} > b c^{2}$ ，则 $a > b$ D、若 $a > b$ ，则 $1 - a < 1 - b$

查看试题解析
4. 已知a＜b ，则下列不等式变形错误的是（　　）.

A、 $4 a < 4 b$ B、 $- 2 a + 4 < - 2 b + 4$ C、 $- 4 a > - 4 b$ D、 $3 a - 4 < 3 b - 4$

查看试题解析
5. 下列不等式变形错误的是（）

A、若 $a < b$ ，则 $2 a - 1 < 2 b - 1$ B、若 $a c > b c$ ，则 $a > b$ C、若 $a > b$ ，则 $2 - a < 3 - b$ D、若 $m > n$ ，则 $\frac{m}{a^{2} + 1} > \frac{n}{a^{2} + 1}$

查看试题解析
6. 若实数x和y满足x＞y ，则下列式子中错误的是（）

A、x＋1＞y＋1 B、2x－6＞2y－6 C、－3x＞－3y D、－ $\frac{x}{3}$ ＜－ $\frac{y}{3}$

查看试题解析
7. 如果a-b>0，那么下列不等式不成立的是（）

A、a-2>b-2 B、-2a<-2b C、 $- \frac{1}{2}$ a< $- \frac{1}{2}$ b D、 $\frac{1}{4}$ a< $\frac{1}{4}$ b

查看试题解析
8. 已知 $a > b$ ，下列结论：① $a^{2} > a b$ ；② $a^{2} > b^{2}$ ；③若 $b < 0$ ，则 $a + b < 2 b$ ；④若 $b > 0$ ，则 $\frac{1}{a} < \frac{1}{b}$ ，其中正确的个数是（）

A、1 B、2 C、3 D、4

查看试题解析
9. 若﹣3a＞1，两边都除以﹣3，得（）

A、a＜﹣ $\frac{1}{3}$ B、a＞﹣ $\frac{1}{3}$ C、a＜﹣3 D、a＞﹣3

查看试题解析
10. 已知 $- \frac{1}{2}$ a ≥b，则a ≤－2b，其根据是（）

A、不等式的两边都加上（或减去）同一个整式，不等号的方向不变 B、不等式的两边都乘以（或除以）同一个正数，不等号的方向不变 C、不等式的两边都乘以（或除以）同一个负数，不等号的方向改变 D、以上答案均不对

查看试题解析

二、填空题

11. 若 $a > b$ ，则 $- 3 a + 1$ $- 3 b + 1$ （用“＜”或“＞”填空）

查看试题解析
12. 已知a＞b ，则 $- \frac{1}{2} a + c$ $- \frac{1}{2} b + c$ （填＞、＜或＝）．

查看试题解析
13. 关于 $x$ 的不等式 $a x > b + 1$ 的解集为 $x < - 1$ ，请写出一组满足条件的实数a，b的值：a＝，b＝．

查看试题解析
14. 若a＜b ，则﹣ $\frac{a}{2}$ +1﹣ $\frac{b}{2}$ +1（填“＞”或“＜”）．

查看试题解析
15. 已知 $a < b$ ， $b < 2 a - 1$ ，则 $a$ 的取值范围为.

查看试题解析
16. 若不等式（1-a）x > 1-a的解集是x< 1，则a的取值范围是

查看试题解析

三、解答题

17. 某数学兴趣小组在学习“不等式的性质”时，有两名同学的对话如下：

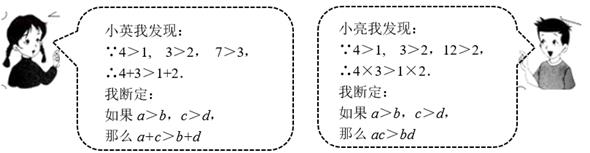
你认为小英和小亮的结论正确吗？如果正确，请说明理由；如果不正确，请举出一个反例。

查看试题解析
18. 3a 一定大于 a 吗？请说明理由

查看试题解析
19. 现有不等式的两个性质：
①在不等式的两边都加上(或减去)同一个整式，不等号的方向不变；

②在不等式的两边都乘以同一个数(或整式)，乘的数(或整式)为正时不等号的方向不变，乘的数(或整式)为负时不等号的方向改变．

请解决以下两个问题：

(1)、利用性质①比较2a与a的大小(a≠0)；

(2)、利用性质②比较2a与a的大小(a≠0)．

查看试题解析
20. 已知a＜0，-1＜b＜0，试比较a、ab、ab²的大小．

查看试题解析
21. 利用不等式性质将不等式化成“x>a”或“x<a”形式：

(1)、6x-4≥2

(2)、1-2x>9

查看试题解析
22. 若2a+b=12，其中a≥0，b≥0，又P=3a+2b．试确定P的最小值和最大值．

查看试题解析
23. 已知 $(a + 1) (b + 2) ⩾ (a + 1) (c + 1)$ ，其中a，b，c是常数，且 $c \neq 1$ .

(1)、当 $b = - 2, c = 3$ 时，求a的范围.

(2)、当 $a < - 2$ 时，比较b和c的大小.

(3)、若当 $a > - 1$ 时， $b ⩽ c - 1$ 成立，则 $\frac{b}{c - 1}$ 的值是多少？

查看试题解析