陕西省初中数学历年真题汇编5 圆及其性质
试卷更新日期：2021-08-11 类型：二轮复习
一、单选题
-
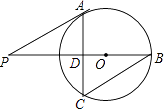
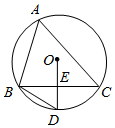
1. 如图，△ABC内接于⊙O，∠A＝50°.E是边BC的中点，连接OE并延长，交⊙O于点D，连接BD，则∠D的大小为（ ）
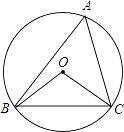
A、55° B、65° C、60° D、75°2.如图，⊙O的半径为4，△ABC是⊙O的内接三角形，连接OB、OC．若∠BAC与∠BOC互补，则弦BC的长为（ ）
A、3 B、4 C、5 D、63. 如图，AB是⊙O的直径，EF，EB是⊙O的弦，且EF=EB，EF与AB交于点C，连接OF，若∠AOF=40°，则∠F的度数是（ ）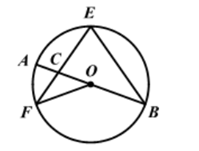
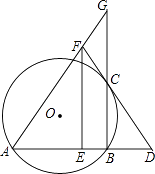
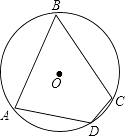
A、20° B、35° C、40° D、55°4. 如图，△ABC是⊙O的内接三角形，AB＝AC，∠BCA＝65°，作CD∥AB，并与○O相交于点D，连接BD，则∠DBC的大小为（ ）
A、15° B、35° C、25° D、45°5. 如图，在△ABC中，AC＝8，∠ABC＝60°，∠C＝45°，AD⊥BC，垂足为D，∠ABC的平分线交AD于点E，则AE的长为（ ）
A、 B、2 C、 D、3二、填空题
-
6. 如图，在圆内接四边形ABCD中，若∠A，∠B，∠C的度数之比为4：3：5，则∠D的度数是°．
7. 如图，正方形 的边长为4， 的半径为1.若 在正方形 内平移（ 可以与该正方形的边相切），则点A到 上的点的距离的最大值为.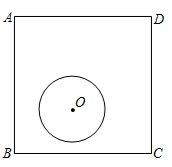
8. 若正六边形的边长为3，则其较长的一条对角线长为.
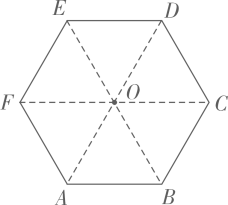9. 如图，在正五边形ABCDE中，AC与BE相交于点F，则
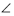AFE的度数为
10. △ABC中，∠C为直角，AB=2，则这个三角形的外接圆半径为 ．三、综合题
-
11. 如图， 是 的直径，点E、F在 上，且 ，连接 、 ，过点 作 的切线，分别与 、 的延长线交于点C、D.
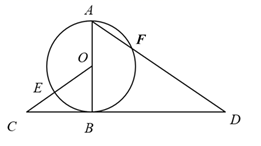
(1)、求证： ；(2)、若 ， ，求线段 的长.12. 如图，△ABC是⊙O的内接三角形，∠BAC＝75°，∠ABC＝45°.连接AO并延长，交⊙O于点D，连接BD.过点C作⊙O的切线，与BA的延长线相交于点E.
(1)、求证：AD∥EC；(2)、若AB＝12，求线段EC的长.13. 如图，AC是⊙O的一条弦，AP是⊙O的切线。作BM=AB并与AP交于点M，延长MB交AC于点E，交⊙O于点D，连接AD.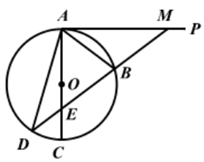
(1)、求证：AB=BE；(2)、若⊙O的半径R=5，AB=6，求AD的长.14. 如图，在Rt△ABC中，∠ACB＝90°，以斜边AB上的中线CD为直径作⊙O，分别与AC、BC相交于点M、N．
(1)、过点N作⊙O的切线NE与AB相交于点E，求证：NE⊥AB；(2)、连接MD，求证：MD＝NB．15. 如图，在△ABC中，∠ACB=90°，O是边AC上一点，以O为圆心，OA为半径的圆分别交AB，AC于点E，D，在BC的延长线上取点F，使得BF=EF，EF与AC交于点G．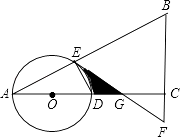
(1)、试判断直线EF与⊙O的位置关系，并说明理由；(2)、若OA=2，∠A=30°，求图中阴影部分的面积．
