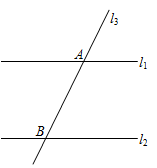陕西省初中数学历年真题汇编4 基本图形性质
试卷更新日期:2021-08-11 类型:二轮复习
一、单选题
-
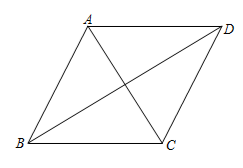
1. 如图,在菱形 中, ,连接 、 ,则 的值为( )
 A、 B、 C、 D、2. 如图,点D、E分别在线段 、 上,连接 、 .若 , , ,则 的大小为( )
A、 B、 C、 D、2. 如图,点D、E分别在线段 、 上,连接 、 .若 , , ,则 的大小为( )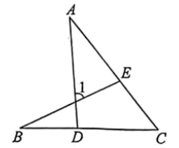 A、60° B、70° C、75° D、85°3. 如图, 、 、 、 是四根长度均为5cm的火柴棒,点A、C、E共线.若 , ,则线段 的长度为( )
A、60° B、70° C、75° D、85°3. 如图, 、 、 、 是四根长度均为5cm的火柴棒,点A、C、E共线.若 , ,则线段 的长度为( )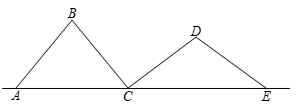 A、6 cm B、7 cm C、 D、8cm4. 若∠A=23°,则∠A余角的大小是( )A、57° B、67° C、77° D、157°5. 如图,在▱ABCD中,AB=5,BC=8.E是边BC的中点,F是▱ABCD内一点,且∠BFC=90°.连接AF并延长,交CD于点G.若EF∥AB,则DG的长为( )
A、6 cm B、7 cm C、 D、8cm4. 若∠A=23°,则∠A余角的大小是( )A、57° B、67° C、77° D、157°5. 如图,在▱ABCD中,AB=5,BC=8.E是边BC的中点,F是▱ABCD内一点,且∠BFC=90°.连接AF并延长,交CD于点G.若EF∥AB,则DG的长为( )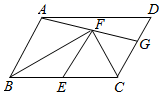 A、 B、 C、3 D、26. 如图,在3×3的网格中,每个小正方形的边长均为1,点A,B,C都在格点上,若BD是△ABC的高,则BD的长为( )
A、 B、 C、3 D、26. 如图,在3×3的网格中,每个小正方形的边长均为1,点A,B,C都在格点上,若BD是△ABC的高,则BD的长为( )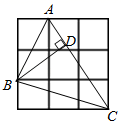 A、 B、 C、 D、7. 如图,在矩形ABCD中,AB=3,BC=6,若点E,F分别在AB,CD上,且BE=2AE,DF=2FC,G,H分别是AC的三等分点,则四边形EHFG的面积为( )
A、 B、 C、 D、7. 如图,在矩形ABCD中,AB=3,BC=6,若点E,F分别在AB,CD上,且BE=2AE,DF=2FC,G,H分别是AC的三等分点,则四边形EHFG的面积为( )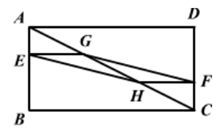 A、1 B、 C、2 D、48. 如图,OC是∠AOB的角平分线,l//OB,若∠1=52°,则∠2的度数为( )
A、1 B、 C、2 D、48. 如图,OC是∠AOB的角平分线,l//OB,若∠1=52°,则∠2的度数为( )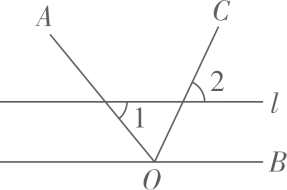 A、52° B、54° C、64° D、69°9. 如图,是一个几何体的表面展开图,则该几何体是( )
A、52° B、54° C、64° D、69°9. 如图,是一个几何体的表面展开图,则该几何体是( )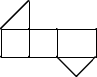 A、正方体 B、长方体 C、三棱柱 D、四棱锥10. 如图,若l1∥l2 , l3∥l4 , 则图中与∠1互补的角有( )
A、正方体 B、长方体 C、三棱柱 D、四棱锥10. 如图,若l1∥l2 , l3∥l4 , 则图中与∠1互补的角有( ) A、1个 B、2个 C、3个 D、4个11. 如图,在菱形ABCD中,点E,F,G,H分别是边AB,BC,CD和DA的中点,连接EF,FG,GH和HE,若EH=2EF,则下列结论正确的是( )
A、1个 B、2个 C、3个 D、4个11. 如图,在菱形ABCD中,点E,F,G,H分别是边AB,BC,CD和DA的中点,连接EF,FG,GH和HE,若EH=2EF,则下列结论正确的是( ) A、AB= EF B、AB=2EF C、AB= EF D、AB= EF12. 如图,直线a∥b,Rt△ABC的直角顶点B落在直线a上,若∠1=25°,则∠2的大小为( )
A、AB= EF B、AB=2EF C、AB= EF D、AB= EF12. 如图,直线a∥b,Rt△ABC的直角顶点B落在直线a上,若∠1=25°,则∠2的大小为( ) A、55° B、75° C、65° D、85°13. 如图,将两个大小、形状完全相同的△ABC和△A′B′C′拼在一起,其中点A′与点A重合,点C′落在边AB上,连接B′C.若∠ACB=∠AC′B′=90°,AC=BC=3,则B′C的长为( )
A、55° B、75° C、65° D、85°13. 如图,将两个大小、形状完全相同的△ABC和△A′B′C′拼在一起,其中点A′与点A重合,点C′落在边AB上,连接B′C.若∠ACB=∠AC′B′=90°,AC=BC=3,则B′C的长为( ) A、3 B、6 C、3 D、14. 如图,在矩形ABCD中,AB=2,BC=3.若点E是边CD的中点,连接AE,过点B作BF⊥AE交AE于点F,则BF的长为( )
A、3 B、6 C、3 D、14. 如图,在矩形ABCD中,AB=2,BC=3.若点E是边CD的中点,连接AE,过点B作BF⊥AE交AE于点F,则BF的长为( ) A、 B、 C、 D、15. 如图,在正方形ABCD中,连接BD,点O是BD的中点,若M、N是边AD上的两点,连接MO、NO,并分别延长交边BC于两点M′、N′,则图中的全等三角形共有( )
A、 B、 C、 D、15. 如图,在正方形ABCD中,连接BD,点O是BD的中点,若M、N是边AD上的两点,连接MO、NO,并分别延长交边BC于两点M′、N′,则图中的全等三角形共有( )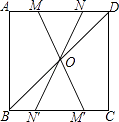 A、2对 B、3对 C、4对 D、5对16. 如图,在△ABC中,∠ABC=90°,AB=8,BC=6.若DE是△ABC的中位线,延长DE交△ABC的外角∠ACM的平分线于点F,则线段DF的长为( )
A、2对 B、3对 C、4对 D、5对16. 如图,在△ABC中,∠ABC=90°,AB=8,BC=6.若DE是△ABC的中位线,延长DE交△ABC的外角∠ACM的平分线于点F,则线段DF的长为( )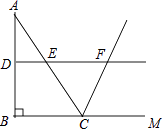 A、7 B、8 C、9 D、1017.
A、7 B、8 C、9 D、1017.如图,AB∥CD,AE平分∠CAB交CD于点E,若∠C=50°,则∠AED=( )
 A、65° B、115° C、125° D、130°
A、65° B、115° C、125° D、130°二、填空题
-
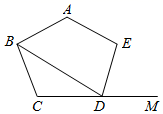
18. 正九边形一个内角的度数为.19. 如图,在正五边形ABCDE中,DM是边CD的延长线,连接BD,则∠BDM的度数是.
 20. 如图,在菱形ABCD中,AB=6,∠B=60°,点E在边AD上,且AE=2.若直线l经过点E,将该菱形的面积平分,并与菱形的另一边交于点F,则线段EF的长为.
20. 如图,在菱形ABCD中,AB=6,∠B=60°,点E在边AD上,且AE=2.若直线l经过点E,将该菱形的面积平分,并与菱形的另一边交于点F,则线段EF的长为. 21. 如图,在正方形ABCD中,AB=8,AC与BD交于点O,N是AO的中点,点M在BC边上,且BM=6. P为对角线BD上一点,则PM—PN的最大值为.
21. 如图,在正方形ABCD中,AB=8,AC与BD交于点O,N是AO的中点,点M在BC边上,且BM=6. P为对角线BD上一点,则PM—PN的最大值为. 22. 点O是平行四边形ABCD的对称中心,AD>AB,E、F分别是AB边上的点,且EF= AB;G、H分别是BC边上的点,且GH= BC;若S1 , S2分别表示∆EOF和∆GOH的面积,则S1 , S2之间的等量关系是
22. 点O是平行四边形ABCD的对称中心,AD>AB,E、F分别是AB边上的点,且EF= AB;G、H分别是BC边上的点,且GH= BC;若S1 , S2分别表示∆EOF和∆GOH的面积,则S1 , S2之间的等量关系是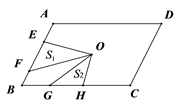 23. 如图,在Rt△ABC中,∠ACB=90°,点D,E分别是AB,AC的中点,点F是AD的中点.若AB=8,则EF= .
23. 如图,在Rt△ABC中,∠ACB=90°,点D,E分别是AB,AC的中点,点F是AD的中点.若AB=8,则EF= .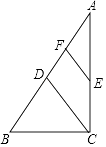 24. 如图,在四边形ABCD中,AB=AD,∠BAD=∠BCD=90°,连接AC.若AC=6,则四边形ABCD的面积为 .
24. 如图,在四边形ABCD中,AB=AD,∠BAD=∠BCD=90°,连接AC.若AC=6,则四边形ABCD的面积为 .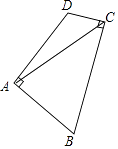 25. 如图,在菱形ABCD中,∠ABC=60°,AB=2,点P是这个菱形内部或边上的一点,若以点P、B、C为顶点的三角形是等腰三角形,则P、D(P、D两点不重合)两点间的最短距离为 .
25. 如图,在菱形ABCD中,∠ABC=60°,AB=2,点P是这个菱形内部或边上的一点,若以点P、B、C为顶点的三角形是等腰三角形,则P、D(P、D两点不重合)两点间的最短距离为 .
三、解答题
-
26. 如图, , ,点 在 上,且 .求证: .
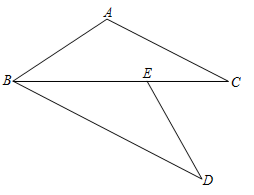 27. 如图,在四边形ABCD中,AD∥BC,∠B=∠C.E是边BC上一点,且DE=DC.求证:AD=BE.
27. 如图,在四边形ABCD中,AD∥BC,∠B=∠C.E是边BC上一点,且DE=DC.求证:AD=BE.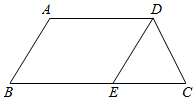 28. 如图,点A,E,F,B在直线l上,AE=BF,AC//BD,且AC=BD,求证:CF=DE
28. 如图,点A,E,F,B在直线l上,AE=BF,AC//BD,且AC=BD,求证:CF=DE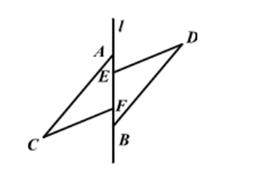 29. 如图,AB∥CD,E、F分别为AB、CD上的点,且EC∥BF,连接AD,分别与EC、BF相交与点G、H,若AB=CD,求证:AG=DH.
29. 如图,AB∥CD,E、F分别为AB、CD上的点,且EC∥BF,连接AD,分别与EC、BF相交与点G、H,若AB=CD,求证:AG=DH.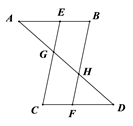 30. 已知:如图,在平行四边形ABCD中,AE⊥BD,CF⊥BD,垂足分别为E,F.求证:△ADE≌△CBF.
30. 已知:如图,在平行四边形ABCD中,AE⊥BD,CF⊥BD,垂足分别为E,F.求证:△ADE≌△CBF.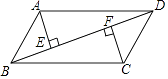 31. 如图,在正方形ABCD中,E,F分别为边AD和CD上的点,且AE=CF,连接AF,CE交于点G.求证:AG=CG.
31. 如图,在正方形ABCD中,E,F分别为边AD和CD上的点,且AE=CF,连接AF,CE交于点G.求证:AG=CG. 32. 如图,在▱ABCD中,连接BD,在BD的延长线上取一点E,在DB的延长线上取一点F,使BF=DE,连接AF、CE.
32. 如图,在▱ABCD中,连接BD,在BD的延长线上取一点E,在DB的延长线上取一点F,使BF=DE,连接AF、CE.求证:AF∥CE.

四、作图题
-
33. 如图,已知直线 ,直线 分别与 、 交于点 、 .请用尺规作图法,在线段 上求作点 ,使点 到 、 的距离相等.(保留作图痕迹,不写作法)