辽宁省沈阳市于洪区2020-2021学年七年级下学期数学期末试卷
试卷更新日期:2021-08-10 类型:期末考试
一、单选题
-
1. 下列手机软件图标中,是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下面每组数分别是三根小木棒的长度,它们能摆成三角形的是( )A、5,1,3 B、2,4,2 C、3,3,7 D、2,3,43. 下列计算中,正确的是( )A、(x4)3=x12 B、a2·a5=a10 C、(3a)2=6a2 D、a6÷a2=a34. 如图,直线AB、CD相交于O , 射线OM平分∠AOC , ON⊥OM , 若∠AOM=35°,则∠CON的度数为( )
2. 下面每组数分别是三根小木棒的长度,它们能摆成三角形的是( )A、5,1,3 B、2,4,2 C、3,3,7 D、2,3,43. 下列计算中,正确的是( )A、(x4)3=x12 B、a2·a5=a10 C、(3a)2=6a2 D、a6÷a2=a34. 如图,直线AB、CD相交于O , 射线OM平分∠AOC , ON⊥OM , 若∠AOM=35°,则∠CON的度数为( ) A、35° B、45° C、55° D、65°5. 下列事件中,是必然事件的是( )
A、35° B、45° C、55° D、65°5. 下列事件中,是必然事件的是( )
A、任意买一张电影票,座位号是2的倍数 B、13个人中至少有两个人生肖相同 C、车辆随机到达一个路口,遇到红灯 D、明天一定会下雨6. 若(x+2)(x﹣1)=x2+mx+n,则m+n=( )
A、1 B、-2 C、-1 D、27. 如图,货车匀速通过隧道(隧道长大于货车长)时,货车从进入隧道至离开隧道的时间与货车在隧道内的长度之间的关系用图象描述大致是( ) A、
A、 B、
B、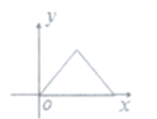 C、
C、 D、
D、 8. 如图,把一块含有30°角(∠A=30°)的直角三角板ABC的直角顶点放在长方形桌面CDEF的一个顶点处,桌面的另一个顶点F在三角板斜边AB上,如果∠1=50°.那么∠AFE=( )
8. 如图,把一块含有30°角(∠A=30°)的直角三角板ABC的直角顶点放在长方形桌面CDEF的一个顶点处,桌面的另一个顶点F在三角板斜边AB上,如果∠1=50°.那么∠AFE=( ) A、10° B、20° C、30° D、40°9. 小明把如图所示的3×3的正方形网格纸板挂在墙上玩飞镖游戏(每次飞镖均落在纸板上,且落在纸板的任何一个点的机会都相等),则飞镖落在阴影区域(四个全等的直角三角形的每个顶点都在格点上)的概率是( )
A、10° B、20° C、30° D、40°9. 小明把如图所示的3×3的正方形网格纸板挂在墙上玩飞镖游戏(每次飞镖均落在纸板上,且落在纸板的任何一个点的机会都相等),则飞镖落在阴影区域(四个全等的直角三角形的每个顶点都在格点上)的概率是( ) A、 B、 C、 D、10. 如图,在△ABC中,AB=4,AC=6,∠ABC和∠ACB的平分线交于O点,过点O作BC的平行线交AB于M点,交AC于N点,则△AMN的周长为( )
A、 B、 C、 D、10. 如图,在△ABC中,AB=4,AC=6,∠ABC和∠ACB的平分线交于O点,过点O作BC的平行线交AB于M点,交AC于N点,则△AMN的周长为( ) A、7 B、8 C、9 D、10
A、7 B、8 C、9 D、10二、填空题
-
11. 纳米是长度度量单位.1纳米(nm)=1.0×10﹣9米,新型冠状病毒的直径平均为100纳米.100纳米这个数据用科学记数法可表示为米.12. 角 等于它的余角的一半,则角 的度数是.13. 若长方形的面积是6a3+5ab+3a , 长为3a , 则它的宽为 .14. 某水果店卖出的香蕉数量(千克)与售价(元)之间的关系如表:
数量(千克)
1
1.5
2
2.5
3
……
售价(元)
3
4.5
6
7.5
9
……
如果卖出的香蕉数量用x(千克)表示,售价用y(元)表示,则y与x的关系式为 .
15. 如图,D是△ABC的边BC上任意一点,E、F分别是线段AD、CE的中点.若△ABC的面积为m , 则△BEF的面积为 . 16. 如图,点P是∠AOB内任意一点,OP=9,M、N分别是射线OA和OB上的动点,若△PMN周长的最小值为9,则∠AOB=°.
16. 如图,点P是∠AOB内任意一点,OP=9,M、N分别是射线OA和OB上的动点,若△PMN周长的最小值为9,则∠AOB=°.
三、解答题
-
17.(1)、计算:(﹣2x2y)2•3xy÷(﹣6x2y).(2)、利用整式乘法公式计算:3.52+7×1.5+1.52 .18. 计算:(﹣1)2021﹣(3.14﹣π)0+( )﹣3 .19. 先化简,再求值: ,其中 .20. 在一个不透明的布袋中装有8个红球和16个白球,它们除颜色不同外其余都相同.(1)、求从布袋中摸出一个球是红球的概率;(2)、现从布袋中取走若干个白球,并放入相同数目的红球,搅拌均匀后,再从布袋中摸出一个球是红球的概率是 ,问取走了多少个白球?21. 如图,△ABC中∠ACB=90°,将△ABC沿着一条直线折叠后,使点A与点C重合(如图②).
 (1)、在图①中用尺规作出折痕所在的直线l , 保留作图痕迹(不用写作法);(2)、直线l是线段AC的线;(3)、设直线l与AB、AC分别相交于点M、N , 连接CM , 若△CMB的周长是21cm,AB=14cm,求BC的长.22. 如图1,在直角梯形ABCD中,动点P从B点出发,沿B→C→D→A匀速运动,设点P运动的路程为x,△ABP的面积为y,图象如图2所示.
(1)、在图①中用尺规作出折痕所在的直线l , 保留作图痕迹(不用写作法);(2)、直线l是线段AC的线;(3)、设直线l与AB、AC分别相交于点M、N , 连接CM , 若△CMB的周长是21cm,AB=14cm,求BC的长.22. 如图1,在直角梯形ABCD中,动点P从B点出发,沿B→C→D→A匀速运动,设点P运动的路程为x,△ABP的面积为y,图象如图2所示. (1)、在这个变化中,自变量、因变量分别是、;(2)、当点P运动的路程x=4时,△ABP的面积为y=;(3)、求AB的长和梯形ABCD的面积.23. 如图1,为测量池塘宽度AB , 可在池塘外的空地上取任意一点O , 连接AO , BO , 并分别延长至点C , D , 使OC=OA , OD=OB , 连接CD .
(1)、在这个变化中,自变量、因变量分别是、;(2)、当点P运动的路程x=4时,△ABP的面积为y=;(3)、求AB的长和梯形ABCD的面积.23. 如图1,为测量池塘宽度AB , 可在池塘外的空地上取任意一点O , 连接AO , BO , 并分别延长至点C , D , 使OC=OA , OD=OB , 连接CD .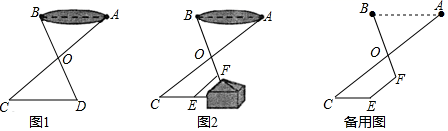 (1)、求证:AB=CD;(2)、如图2,受地形条件的影响,于是采取以下措施:延长AO至点C , 使OC=OA , 过点C作AB的平行线CE , 延长BO至点F , 连接EF , 测得∠CEF=140°,∠OFE=110°,CE=11m,EF=10m,求出池塘AB的宽度.24. 数学活动课上,张老师准备了若干个如图①的三种纸片,A种纸片是边长为a的正方形,B种纸片是边长为b的正方形,C种纸片是长为b , 宽为a的长方形,并用A种纸片一张,B种纸片一张,C种纸片两张拼成如图②的大正方形.
(1)、求证:AB=CD;(2)、如图2,受地形条件的影响,于是采取以下措施:延长AO至点C , 使OC=OA , 过点C作AB的平行线CE , 延长BO至点F , 连接EF , 测得∠CEF=140°,∠OFE=110°,CE=11m,EF=10m,求出池塘AB的宽度.24. 数学活动课上,张老师准备了若干个如图①的三种纸片,A种纸片是边长为a的正方形,B种纸片是边长为b的正方形,C种纸片是长为b , 宽为a的长方形,并用A种纸片一张,B种纸片一张,C种纸片两张拼成如图②的大正方形.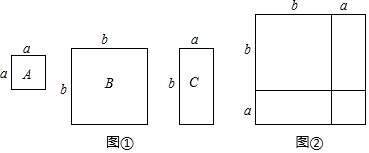 (1)、观察图②,写出代数式(a+b)2 , a2+b2 , ab之间的等量关系是;(2)、根据(1)中的等量关系,解决下列问题;
(1)、观察图②,写出代数式(a+b)2 , a2+b2 , ab之间的等量关系是;(2)、根据(1)中的等量关系,解决下列问题;①已知a+b=4,a2+b2=10,求ab的值;
②已知(x﹣2021)2+(x﹣2019)2=130,直接写出x﹣2020的值.
25. 如图,已知AB∥CD , P是直线AB , CD间的一点,PF⊥CD于点F , PE交AB于点E , ∠FPE=120°. (1)、求∠AEP的度数;(2)、射线PN从PF出发,以每秒30°的速度绕P点按逆时针方向旋转,当PN垂直AB时,立刻按原速返回至PF后停止运动;射线EM从EA出发,以每秒15°的速度绕E点按逆时针方向旋转至EB后停止运动,若射线PN , 射线EM同时开始运动,设运动时间为t秒.
(1)、求∠AEP的度数;(2)、射线PN从PF出发,以每秒30°的速度绕P点按逆时针方向旋转,当PN垂直AB时,立刻按原速返回至PF后停止运动;射线EM从EA出发,以每秒15°的速度绕E点按逆时针方向旋转至EB后停止运动,若射线PN , 射线EM同时开始运动,设运动时间为t秒.①当∠MEP=15°时,求∠EPN的度数;
②当EM∥PN时,直接写出t的值.