辽宁省丹东市2020-2021学年七年级下学期数学期末试卷
试卷更新日期:2021-08-10 类型:期末考试
一、单选题
-
1. 观察下列平面图形,其中是轴对称图形的有( )
 A、1个 B、2个 C、3个 D、4个2. 一个袋子中装有只有标号不同的五张卡片,号分别为1、2、3、4、5,随机抽出1张,必然事件是( )A、标号小于6 B、标号大于6 C、标号是奇数 D、标号是33. 下列计算正确的是( )A、x2•x3=x6 B、4x2+4x3=8x5 C、(a2)4=a6 D、(x2y)2+x4y2=2x4y24. 下列长度的三条线段,不能作为三角形的三边的是( )A、5,12,13 B、6,8,10 C、5,5,10 D、3,3,55. 如图,下列能判定AB∥CD的条件有( )
A、1个 B、2个 C、3个 D、4个2. 一个袋子中装有只有标号不同的五张卡片,号分别为1、2、3、4、5,随机抽出1张,必然事件是( )A、标号小于6 B、标号大于6 C、标号是奇数 D、标号是33. 下列计算正确的是( )A、x2•x3=x6 B、4x2+4x3=8x5 C、(a2)4=a6 D、(x2y)2+x4y2=2x4y24. 下列长度的三条线段,不能作为三角形的三边的是( )A、5,12,13 B、6,8,10 C、5,5,10 D、3,3,55. 如图,下列能判定AB∥CD的条件有( )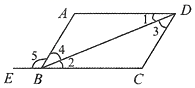
①∠C+∠ABC=180°;②∠2=∠3;③∠1=∠2;④∠C=∠5;⑤∠4=∠3
A、1个 B、2个 C、3个 D、4个6. 用直尺和圆规作一个角的平分线的示意图如图所示,则能说明∠AOC=∠BOC的依据是( )
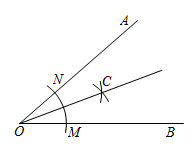 A、SSS B、ASA C、AAS D、SAS7. 如图,AD平分∠BAC,AE⊥BC,∠B=45°,∠C=73°,则∠DAE的度数是( )
A、SSS B、ASA C、AAS D、SAS7. 如图,AD平分∠BAC,AE⊥BC,∠B=45°,∠C=73°,则∠DAE的度数是( ) A、62 B、31 C、17 D、148. 如图,均匀地向一个容器内注水,在注满水的过程中,水的体积V与水的高度h之间关系的大致图象是( )
A、62 B、31 C、17 D、148. 如图,均匀地向一个容器内注水,在注满水的过程中,水的体积V与水的高度h之间关系的大致图象是( )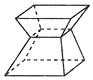 A、
A、 B、
B、 C、
C、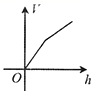 D、
D、 9. 已知:(2021﹣a)(2020﹣a)=4,则(2021﹣a)2+(2020﹣a)2的值为( )A、7 B、8 C、9 D、12
9. 已知:(2021﹣a)(2020﹣a)=4,则(2021﹣a)2+(2020﹣a)2的值为( )A、7 B、8 C、9 D、12二、填空题
-
10. 一张纸的厚度约为0.000 008 57米,用科学记数法表示其结果是米.11. 若 ,则a+b= .12. 等腰三角形的一边长为3,另一边长为6,则该三角形的周长是 .13. 如图是由6个边长相等的正方形组合成的图形,∠1+∠2+∠3= .
 14. 如图,要测量河岸相对的两点A、B之间的距离,已知AB垂直于河岸BF , 现在BF上取两点C、D , 使CD=CB , 过点D作BF的垂线ED , 使点A、C、E在一条直线上,若ED=65米,则AB的长是 .
14. 如图,要测量河岸相对的两点A、B之间的距离,已知AB垂直于河岸BF , 现在BF上取两点C、D , 使CD=CB , 过点D作BF的垂线ED , 使点A、C、E在一条直线上,若ED=65米,则AB的长是 . 15. 多项式 是完全平方式,则k= .16. 已知(x+1)(x﹣2)=x2+mx+n,则m+n=17.
15. 多项式 是完全平方式,则k= .16. 已知(x+1)(x﹣2)=x2+mx+n,则m+n=17.如图,在四边形ABCD中,∠A=90°,AD=8.对角线BD⊥CD,P是BC边上一动点,连结PD.若∠ADB=∠C,则PD长的最小值为 .
 18. 已知MN是线段AB的垂直平分线,P、Q是直线MN上两点,且∠PAB=35°,∠QBA=60°,则∠QAP的度数为 .
18. 已知MN是线段AB的垂直平分线,P、Q是直线MN上两点,且∠PAB=35°,∠QBA=60°,则∠QAP的度数为 .三、解答题
-
19.(1)、 ;(2)、x3•(2x3)4÷(﹣x4)3 .20. 先化简,再求值:[(a﹣2b)2﹣(a+2b)(a﹣2b)]÷4b , 其中a=﹣2,b=1.21. 已知:AB∥CD , O为AD中点.
 (1)、请判断△AOB与△DOC是否全等?并说明理由;(2)、若BD=CD , 请判断AD与BC的位置关系,并说明理由.22. 一个不透明的袋中装有5个黄球,13个黑球和22个红球,它们除颜色外都相同.(1)、小明和小红玩摸球游戏,规定每人摸球后再将摸到的球放回去为一次游戏.若摸到黑球小明获胜,摸到黄球小红获胜,这个游戏对双方公平吗?请说明你的理由;(2)、现在裁判想从袋中取出若干个黑球,并放入相同数量的黄球,使得这个游戏对双方公平,问取出了多少黑球?23. 如图,已知△ABC(AC<BC),请用尺规作图的方法在BC上作一点P , 使PA+PC=BC(保留作图痕迹,不用写出作法).
(1)、请判断△AOB与△DOC是否全等?并说明理由;(2)、若BD=CD , 请判断AD与BC的位置关系,并说明理由.22. 一个不透明的袋中装有5个黄球,13个黑球和22个红球,它们除颜色外都相同.(1)、小明和小红玩摸球游戏,规定每人摸球后再将摸到的球放回去为一次游戏.若摸到黑球小明获胜,摸到黄球小红获胜,这个游戏对双方公平吗?请说明你的理由;(2)、现在裁判想从袋中取出若干个黑球,并放入相同数量的黄球,使得这个游戏对双方公平,问取出了多少黑球?23. 如图,已知△ABC(AC<BC),请用尺规作图的方法在BC上作一点P , 使PA+PC=BC(保留作图痕迹,不用写出作法). 24. 如图1是一个大长方形减去一个小长方形后形成的图形,已知动点P以1cm/s的速度沿边框A→B→C→D→E→F的路径移动,相应的△AFP的面积S(cm2)与时间x(s)之间的关系如图2,若AF=3cm,请求出:
24. 如图1是一个大长方形减去一个小长方形后形成的图形,已知动点P以1cm/s的速度沿边框A→B→C→D→E→F的路径移动,相应的△AFP的面积S(cm2)与时间x(s)之间的关系如图2,若AF=3cm,请求出: (1)、图1中的BC的长是多少?(2)、图2中的a是多少?(3)、图1中的图形面积是多少?(4)、图2中的b是多少?25. 已知:AB∥CD .
(1)、图1中的BC的长是多少?(2)、图2中的a是多少?(3)、图1中的图形面积是多少?(4)、图2中的b是多少?25. 已知:AB∥CD . (1)、探究∠B、∠BED、∠D之间的数量关系,并说明理由;(2)、利用上述中的结论,
(1)、探究∠B、∠BED、∠D之间的数量关系,并说明理由;(2)、利用上述中的结论,①如图2,已知AB∥CD , 试探究∠E、∠G、∠B、∠F、∠D之间的数量关系,并说明理由;
②如图3,已知AB∥CD , 请直接写出∠B、∠D、∠E1、∠E2……∠En、∠F1、∠F2…∠Fn+1之间的数量关系.
26. 如图,在△ABC中,∠ACB=90°,CD⊥AB于点D , BO平分∠DBC , 交CD于点O , E为AB上一点,连接OE , 且OE∥AC . (1)、∠A与∠BCD相等吗?请说明理由;(2)、△BOE与△BOC是否全等?为什么?(3)、若BC=5,AC=12,BD ,求出△ACE的面积.
(1)、∠A与∠BCD相等吗?请说明理由;(2)、△BOE与△BOC是否全等?为什么?(3)、若BC=5,AC=12,BD ,求出△ACE的面积.