河北省张家口市宣化区2020-2021学年七年级下学期数学期末试卷
试卷更新日期:2021-08-10 类型:期末考试
一、单选题
-
1. 下列命题中,是假命题的是( )A、两点之间,线段最短 B、对顶角相等 C、同旁内角互补 D、直角的补角仍然是直角2. 目前世界上强大的显微镜的观测极限为0.0000000027mm,数据0.0000000027用科学记数法表示为( )A、 B、 C、 D、3. 下列图形中,能确定 的是( )A、
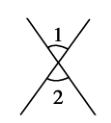 B、
B、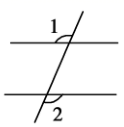 C、
C、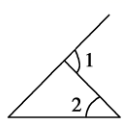 D、
D、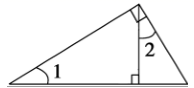 4. 下列因式分解正确的是( )A、 B、 C、 D、5. 已知 是方程2x﹣ay=3的一组解,那么a的值为( )A、﹣1 B、3 C、﹣3 D、﹣156. 如图所示,△ABC中AC边上的高线是( )
4. 下列因式分解正确的是( )A、 B、 C、 D、5. 已知 是方程2x﹣ay=3的一组解,那么a的值为( )A、﹣1 B、3 C、﹣3 D、﹣156. 如图所示,△ABC中AC边上的高线是( ) A、线段DA B、线段BA C、线段BD D、线段BC7. 已知三角形三边长分别为3、x、10,若x为正整数,则这样的三角形个数为( )A、 B、 C、 D、8. 对不等式 ,给出了以下解答:
A、线段DA B、线段BA C、线段BD D、线段BC7. 已知三角形三边长分别为3、x、10,若x为正整数,则这样的三角形个数为( )A、 B、 C、 D、8. 对不等式 ,给出了以下解答:①去分母,得 ;②去括号,得 ;③移项、合并同类项,得 ;④两边都除以3,得 其中错误开始的一步是( )
A、① B、② C、③ D、④9. 当n为自然数时,(n+1)2-(n-3)2一定能被下列哪个数整除( )A、5 B、6 C、7 D、810. 对于任意的底数 , ,当 是正整数时,第一步变形 第二步变形其中,第二步变形的依据是( )
A、乘法交换律与结合律 B、乘法交换律 C、乘法结合律 D、乘方的定义11.如图,下列判断中错误的是( )
 A、由∠A+∠ADC=180°得到AB∥CD B、由AB∥CD得到∠ABC+∠C=180° C、由∠1=∠2得到AD∥BC D、由AD∥BC得到∠3=∠412. 已知直线AB,CB,l在同一平面内,若AB⊥l,垂足为B,CB⊥l,垂足也为B,则正确的图形可以是( )A、
A、由∠A+∠ADC=180°得到AB∥CD B、由AB∥CD得到∠ABC+∠C=180° C、由∠1=∠2得到AD∥BC D、由AD∥BC得到∠3=∠412. 已知直线AB,CB,l在同一平面内,若AB⊥l,垂足为B,CB⊥l,垂足也为B,则正确的图形可以是( )A、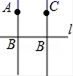 B、
B、 C、
C、 D、
D、 13. 如图, ,则 满足的数量关系是( )
13. 如图, ,则 满足的数量关系是( ) A、 B、 C、 D、14. 如图,是三个等边三角形随意摆放的图形,则∠1+∠2+∠3等于( )
A、 B、 C、 D、14. 如图,是三个等边三角形随意摆放的图形,则∠1+∠2+∠3等于( )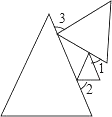 A、90° B、120° C、150° D、180°
A、90° B、120° C、150° D、180°二、填空题
-
15. 计算: .16. 如图是一个长和宽分别为a、b的长方形,它的周长为14、面积为10,则a2b+ab2的值为 .
 17. 有甲、乙、丙三种商品,如果购买甲3件,乙2件,丙1件共需315元钱,购买甲1件,乙2件,丙3件共需285元钱,那么购买甲、乙、丙三种商品各一件共需元钱.18. 若不等式组 的解集是 ,则 .19. 如图,有三种卡片,其中边长为 的正方形卡片1张,长为 、宽为 的长方形卡片4张,边长为 的正方形卡片4张,用这9张卡片刚好能拼成一个大正方形,则这个大正方形的边长为 .
17. 有甲、乙、丙三种商品,如果购买甲3件,乙2件,丙1件共需315元钱,购买甲1件,乙2件,丙3件共需285元钱,那么购买甲、乙、丙三种商品各一件共需元钱.18. 若不等式组 的解集是 ,则 .19. 如图,有三种卡片,其中边长为 的正方形卡片1张,长为 、宽为 的长方形卡片4张,边长为 的正方形卡片4张,用这9张卡片刚好能拼成一个大正方形,则这个大正方形的边长为 . 20. 如图, 面积为1,第一次操作:分别延长 , , 至点 , , ,使 , , ,顺次连接 , , ,得到 .二次操作:分别延长 , , ,至点 , , ,使 , , ,顺次连接 , , ,得到 ,…按此规律,要使得到的三角形的面积超过2021,最少经过次操作.
20. 如图, 面积为1,第一次操作:分别延长 , , 至点 , , ,使 , , ,顺次连接 , , ,得到 .二次操作:分别延长 , , ,至点 , , ,使 , , ,顺次连接 , , ,得到 ,…按此规律,要使得到的三角形的面积超过2021,最少经过次操作.
三、解答题
-
21. 计算:(1)、解不等式组: ,并把解集表示在数轴上;
 (2)、因式分解: .22. 对x , y定义一种新运算T , 规定:T(x , y)=ax+2by-1(其中a , b均为非零常数),这里等式右边是通常的四则运算,例如:T(0,1)=a·0+2b·1-1=2b-1.已知T(1,-1)=-2,T(-3,2)=4.(1)、求a , b的值;(2)、利用(1)的结果化简求值:(a-b)2-(a+2b)·(a-2b)+2a(1+b).23. 如图,已知 , ,点P是射线AM上一动点(与点A不重合),BC,BD分别平分 和 ,分别交射线AM于点C,D.
(2)、因式分解: .22. 对x , y定义一种新运算T , 规定:T(x , y)=ax+2by-1(其中a , b均为非零常数),这里等式右边是通常的四则运算,例如:T(0,1)=a·0+2b·1-1=2b-1.已知T(1,-1)=-2,T(-3,2)=4.(1)、求a , b的值;(2)、利用(1)的结果化简求值:(a-b)2-(a+2b)·(a-2b)+2a(1+b).23. 如图,已知 , ,点P是射线AM上一动点(与点A不重合),BC,BD分别平分 和 ,分别交射线AM于点C,D. (1)、求 的度数(2)、当点P运动时, 的比值是否随之变化?若不变,请求出这个比值;若变化,请找出变化规律;(3)、当点P运动到某处时, ,求此时 的度数.24. 已知 中, 是 的角平分线, , .
(1)、求 的度数(2)、当点P运动时, 的比值是否随之变化?若不变,请求出这个比值;若变化,请找出变化规律;(3)、当点P运动到某处时, ,求此时 的度数.24. 已知 中, 是 的角平分线, , . (1)、如图①,若 于点 ,求 的度数;(2)、如图②,若 为 上一个动点( 不与 , 重合),且 于点 时,则 ;(3)、探究:如图②, 中,已知 , 均为锐角, , 是 的角平分线,若 为线段 上一个动点( 不与 重合),且 于点 时,请写出 与 , 的关系,并说明理由.25. 某商场计划经销A、B两种新型节能台灯共50盏,这两种台灯的进价、售价如表所示:
(1)、如图①,若 于点 ,求 的度数;(2)、如图②,若 为 上一个动点( 不与 , 重合),且 于点 时,则 ;(3)、探究:如图②, 中,已知 , 均为锐角, , 是 的角平分线,若 为线段 上一个动点( 不与 重合),且 于点 时,请写出 与 , 的关系,并说明理由.25. 某商场计划经销A、B两种新型节能台灯共50盏,这两种台灯的进价、售价如表所示:A型
B型
进价(元/盏)
40
65
售价(元/盏)
60
100
(1)、若该商场购进这批台灯共用去2500元,问这两种台灯各购进多少盏?(2)、在每种台灯销售利润不变的情况下,若该商场销售这批台灯的总利润不少于1400元,问至少购进B种台灯多少盏?26. 嘉嘉同学动手剪了如图①所示的正方形与长方形纸片若干张. (1)、问题发现
(1)、问题发现他用1张Ⅰ型、1张Ⅱ型和2张Ⅲ型卡片拼出一个新的图形(如图②).根据图形的面积关系写出一个你所熟悉的乘法公式,这个乘法公式是;
(2)、如果要拼成一个长为a+2b , 宽为a+b的大长方形,那么需要Ⅱ型卡片张,Ⅲ型卡片张.(3)、拓展探究若a+b=5,ab=6,求a2+b2的值;
(4)、当他拼成如图③所示的长方形时,根据图形的面积,可把多项式a2+3ab+2b2分解因式,其结果是 .(5)、解决问题请你依照嘉嘉的方法,利用拼图分解因式:a2+5ab+6b2= .