河北省邯郸市武安市2020-2021学年七年级下学期数学期末试卷

试卷更新日期：2021-08-10 类型：期末考试

进入出卷网下载

一、单选题

1. 下列实数中，是无理数的是（）

A、 $\frac{3}{8}$ B、3.1415 C、 $\sqrt{11}$ D、 $\sqrt[3]{27}$

查看试题解析
2. 下列各数中一定有平方根的是（）

A、a²﹣5 B、﹣a C、a+1 D、a²+1

查看试题解析
3. 为调查某大学新生对学校的满意程度，以下抽样调查最合适的是（）

A、学校新生中的男生 B、学校全体学生 C、学校新生中的女生 D、用新生名单，随机抽取三分之一的新生

查看试题解析
4. 如图，若村庄A要从河流 $l$ 引水入村，则沿着垂线段AB铺设水管最节省材料，其依据是（）

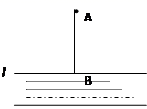A、两点之间，线段最短 B、垂线段最短 C、两点确定一条直线 D、在同一平面内，经过一点有并且只有一条直线与已知直线垂直

查看试题解析
5. 如图，在数轴上．表示的解集用不等式表示为（）

A、2＜x＜4 B、﹣2＜x≤4． C、﹣2≤x＜4 D、﹣2≤x≤4．

查看试题解析
6. 若a＞b ，则下列不等式变形正确的是（）

A、a+5＜b+5 B、 $\frac{a}{3} < \frac{b}{3}$ C、3a﹣2＞3b﹣2 D、﹣4a＞﹣4b

查看试题解析
7. 二元一次方程组 ${\begin{array}{l} 2 x - y = - 3 \\ 4 x + y = 15 \end{array}$ 的解是（）

A、 ${\begin{array}{l} x = 2 \\ y = 1 \end{array}$ B、 ${\begin{array}{l} x = 2 \\ y = - 1 \end{array}$ C、 ${\begin{array}{l} x = 9 \\ y = 21 \end{array}$ D、 ${\begin{array}{l} x = 2 \\ y = 7 \end{array}$

查看试题解析
8. 估计 $\sqrt{68}$ 的值在（）

A、5到6之间 B、6到7之间 C、7到8之间 D、8到9之间

查看试题解析
9. 如图，DE∥BC ， BE平分∠ABC ，若∠1＝66°，则∠CBE的度数为（）

A、33° B、32° C、22° D、56°

查看试题解析
10. 如图，若棋子“炮”的坐标为 $(3 ， 0)$ ，棋子“马”的坐标为 $(1 ， 1)$ ，则棋子“车”的坐标为（）

A、 $(3 ， 2)$ B、 $(- 3 ， 3)$ C、 $(2 ， 2)$ D、 $(- 2 ， 1)$

查看试题解析
11. 已知关于x的不等式2x+m＞-5的解集是x＞-3，那么m的值是（）

A、-2 B、-1 C、0 D、1

查看试题解析
12. 某次考试中，某班级的数学成绩被绘制成了如图所示的频数分布直方图．下列说法错误的是（）

A、得分在70～80分之间的人数最多 B、及格（不低于60分）的人数为26 C、得分在90～100分之间的人数占总人数的5% D、该班的总人数为40

查看试题解析
13. 某玩具车间每天能生产甲种玩具零件100个或乙种玩具零件200个，甲种玩具零件1个与乙种玩具零件2个能组成一个完整的玩具，怎样安排生产才能在30天内组装出最多的玩具？设生产甲种玩具零件x天，生产乙种玩具零件y天，则有（）

A、 ${\begin{array}{l} x + y = 30 \\ 2 \times 200 x = 100 y \end{array}$ B、 ${\begin{array}{l} x + y = 30 \\ 2 \times 100 x = 200 y \end{array}$ C、 ${\begin{array}{l} x + y = 30 \\ 200 x = 100 y \end{array}$ D、 ${\begin{array}{l} x + y = 30 \\ 100 x = 200 y \end{array}$

查看试题解析
14. 已知点 $P (x, y)$ 为第四象限内一点，且满足 $| x | = 3$ ， $y^{2} = 4$ ，则P点的坐标为（）

A、 $(- 3 ， 2)$ B、 $(3,2)$ C、 $(3 ， - 2)$ D、 $(- 3 ， - 2)$

查看试题解析
15. 如图，在△ABC中，BC＝5，∠A＝80°，∠B＝70°，把△ABC沿RS的方向平移到△DEF的位置，若CF＝4，则下列结论中错误的是（）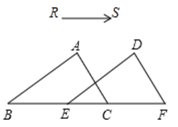

A、BE＝4 B、∠F＝30° C、AB∥DE D、DF＝5

查看试题解析
16. 有四位同学一起研究一道数学题．如图，已知EF⊥AB ， CD⊥AB ．则下列说法正确的是（）
甲说：“如果还知道∠CDG＝∠BFE ，则能得到∠AGD＝∠ACB ． ”

乙说：“把甲的已知和结论倒过来，即由∠AGD＝∠ACB ，可得到∠CDG＝∠BFE ． ”

丙说：“∠AGD一定大于∠BFE ． ”

丁说：“如果连接GF ，则GF一定平行于AB ． ”

A、甲对乙错 B、乙错丁对 C、甲、乙对 D、乙、丙对

查看试题解析

二、填空题

17. 根据数量关系“y与6的和不小于1”列不等式为．

查看试题解析
18. 已知 $x ， y$ 互为相反数且满足二元一次方程组 ${\begin{array}{l} 2 x + 3 y = k ， \\ x + 2 y = - 1 ， \end{array}$ 则 $k$ 的值是．

查看试题解析
19. 在平面直角坐标系中，已知点P（2m+4，m﹣1），试分别根据下列条件，求出点P的坐标：

(1)、当点P在y轴上，点P的坐标为；

(2)、点P的纵坐标比横坐标大3，点P的坐标为；

(3)、点P到两坐标轴的距离相等，点P的坐标为．

查看试题解析

三、解答题

20. 解不等式：x $- \frac{2 - x}{6} \geq \frac{4 x - 2}{3}$ ，把它的解集表示在数轴上，并写出它的最大整数解．

查看试题解析
21. 已知一个正数的两个平方根分别是2a﹣3与a﹣6，3﹣2b的立方根为1，求a+b的平方根．

查看试题解析
22. 解二元一次方程组 ${\begin{matrix} 3 x + y = 1 ① \\ x - 2 y = 12 ② \end{matrix}$

(1)、有同学这么做：由②，得x＝2y＋12③
将③代入①，得3（2y＋12）＋y＝1，解得y＝－5，

将y＝－5代入③，得x＝2，所以这个方程组的解为 ${\begin{matrix} x = 2 \\ y = - 5 \end{matrix}$ ．

该同学解这个方程组的过程中使用了代入消元法，目的是把二元一次方程组转化为．

(2)、请你用加减消元法解该二元一次方程组．

查看试题解析
23. 禹驰商店决定购进A、B两种纪念品．若购进A种纪念品8件，B种纪念品3件，需950元；若购进A种纪念品5件，B种纪念品6件，需800元。

(1)、求购进A、B两种纪念品每件各需多少元？

(2)、若禹驰商店决定购进这两种纪念品共100件，考虑市场需求和资金周转，用于购买这100件纪念品的资金不超过7650元，求禹驰商店至多购进A种纪念品多少件？

查看试题解析
24. 如图，在平面直角坐标系xOy中，三角形ABC三个顶点的坐标分别为A（﹣5，1），B（﹣4，4），C（﹣1，﹣1）．将三角形ABC向右平移5个单位长度，再向下平移4个单位长度，得到三角形A'B'C'，其中点A'，B'，C'分别为点A ， B ， C的对应点．

(1)、请在所给坐标系中画出三角形A'B'C'，并直接写出点C'的坐标；

(2)、若AB边上一点P经过上述平移后的对应点为P'（x ， y），用含x ， y的式子表示点P的坐标；（直接写出结果即可）

(3)、求三角形A'B'C'的面积．

查看试题解析

25. 体育委员统计了全班同学60秒跳绳的次数，列出了频数分布表和频数分布直方图，如图：

次数	频数
$60 ⩽ x < 80$	2
$80 ⩽ x < 100$
$100 ⩽ x < 120$	18
$120 ⩽ x < 140$	13
$140 ⩽ x < 160$	8
$160 ⩽ x < 180$
$180 ⩽ x < 200$	1

(1)、补全频数分布表和频数分布直方图．

(2)、上表中组距是次，组数是组．

(3)、跳组次数在

100 ⩽ x < 120

范围的学生有人，全班共有人．

(4)、若规定跳维次数不低于140次为优秀，求全班同学跳绳的优秀率是多少？

查看试题解析

26. 如图1，已知直线CD∥EF ，点A ， B分别在直线CD与EF上．P为两平行线间一点．

(1)、若∠DAP＝40°，∠FBP＝70°，则∠APB＝

(2)、猜想∠DAP ， ∠FBP ， ∠APB之间有什么关系？并说明理由；

(3)、利用（2）的结论解答：
①如图2，AP₁ ， BP₁分别平分∠DAP ， ∠FBP ，请你写出∠P与∠P₁的数量关系，并说明理由；

②如图3，AP₂ ， BP₂分别平分∠CAP ， ∠EBP ，若∠APB＝β，求∠AP₂B ．（用含β的代数式表示）

查看试题解析