北京市延庆区2020-2021学年七年级下学期数学期末试卷

试卷更新日期：2021-08-10 类型：期末考试

进入出卷网下载

一、单选题

1. 经过了8年的研发，华为正式推出了鸿蒙系统．鸿蒙系统使用了一款新的芯片，这款芯片被命名为麒麟9010，采用的是最为先进的3纳米工艺.3纳米就是0.000003毫米．把0.000003用科学记数法表示为（）

A、3×10⁶ B、3×10^-6 C、3×10^-5 D、3×10⁵

查看试题解析
2. 不等式x﹣2＞0的解集可以在数轴上表示为（）

A、 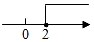B、 C、 D、

查看试题解析
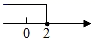3. 下列计算正确的是（）

A、 $(- m n^{2}) \cdot (2 m n) = - 2 m^{2} n^{3}$ B、 $y^{8} \div y^{2} = y^{4}$ C、(a³)⁴= a⁷ D、 $x + x^{2} = x^{3}$

查看试题解析
4. 下列调查方式，你认为最合适的是（）

A、旅客上飞机前的安检，采用抽样调查方式 B、了解端午节到延庆旅游的人数，采用抽样调查方式 C、了解北京市中学生的用眼卫生情况，采用全面调查方式 D、了解一批手机电池的使用寿命，采用全面调查方式

查看试题解析
5. 若m＞n ，则下列不等式不成立的是（）

A、6－m＞6－n B、－3m＜－3n C、m+14＞n+14 D、7m＞7n

查看试题解析
6. 下面从左到右的变形，是正确进行因式分解的为（）

A、 $x^{2} + 6 x + 8 = x (x + 6) + 8$ B、 $(x + 2) (x - 2) = x^{2} - 4$ C、 $x (x + 1) = x^{2} + x$ D、 $x^{2} - 2 x + 1 = {(x - 1)}^{2}$

查看试题解析
7. 下列命题中是假命题的是（）

A、对顶角相等 B、平行于同一条直线的两条直线互相平行 C、同旁内角互补 D、过直线外一点有且只有一条直线与这条直线平行

查看试题解析
8. 如图，点F是∠ACE内一点，FD $//$ AC ， FB $//$ EC ，点D在射线CE上，点B在射线CA上．下列结论正确的是（）
①∠1=∠F；②∠2=∠C；③∠FBC=∠FDC；④∠FBC+∠2 =180°

A、①② B、①②④ C、①②③ D、①②③④

查看试题解析

二、填空题

9. 因式分解： $x^{2} - 6 x + 9$ =.

查看试题解析
10. 写出二元一次方程2x－y=5的一个整数解．

查看试题解析
11. 如图，点O为直线AB上一点，OC⊥OD ，如果∠1＝35°，那么∠2的度数是；

查看试题解析
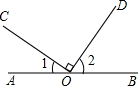12. 若 ${\begin{array}{l} x = 3 ， \\ y = 2 \end{array}$ 是方程 $m x + y - 1 = 0$ 的一组解，则m的值是．

查看试题解析
13. 已知二元一次方程组 ${\begin{array}{l} 2 x - y = - 1 \\ x - 2 y = 4 \end{array}$ ，则 $x - y$ 的值为．

查看试题解析
14. 如图，在三角形ABC中，点D ， E分别在边AC ， BC上，请你添加一个条件，使得DE $//$ AB ．（要求：不再添加辅助线，只需填一个答案即可）

查看试题解析
15. 如图的框图表示解不等式2﹣3x $>$ 4﹣x的流程，其中“系数化为1”这一步骤的依据是．

查看试题解析
16. 观察、归纳：
$(x - 1) (x + 1) = x^{2} - 1$

$(x - 1) (x^{2} + x + 1) = x^{3} - 1$

$(x - 1) (x^{3} + x^{2} + x + 1) = x^{4} - 1$

……

请你根据以上等式的规律，完成下列问题：

(1)、(x-1)(x⁹+…+x²+x+1)= ．

(2)、计算1+3+3²+…+3²⁰²¹= ．

查看试题解析
17. 完成下面的证明．
已知：如图，三角形ABC中，∠B=∠C ，点N在BA的延长线上，且AM $//$ BC ．

求证：AM是∠CAN的角平分线．

证明：∵AM∥BC ，

∴∠B=∠1（         ▲          ），

∠C=∠2（        ▲         ）．

∵∠B=∠C ，

∴∠1=     ▲     ．

∴AM是∠CAN的角平分线（       ▲        ）．

查看试题解析

三、解答题

18. 因式分解：

(1)、 $a^{2} + 2 a$ ；

(2)、 $x^{2} - 16$ ．

查看试题解析
19. 计算：

(1)、 $3^{2} - {(3 - π)}^{0} + 2^{- 1} - | - \frac{1}{2} |$ ；

(2)、 $(a + 2) (a - 3) + {(a + 2)}^{2}$ ．

查看试题解析
20. 解方程组：

(1)、 ${\begin{matrix} x = 5 + y \\ x - 2 y = 2 \end{matrix}$ ；

(2)、 ${\begin{array}{l} 3 x + 2 y = 1 \\ x - 2 y = 3 \end{array}$ ．

查看试题解析
21. 先化简，再求值：
已知 $x^{2} - 2 x - 1 = 2$ ，求代数式 $x (x - 4) + (x - 3) (x + 3)$ 的值．

查看试题解析
22. 解不等式组： ${\begin{array}{l} 3 (x - 1) \leq 5 x + 1 \\ 7 x < \frac{15 - x}{2} \end{array}$ 并写出它的所有整数解．

查看试题解析
23. 已知：点P是三角形ABC内一点．

(1)、①过点P作AC的平行线交AB于点E ，交BC于点F；
②过点P作AB的垂线，垂足为点Q；

(2)、测量∠EPQ=°；

(3)、测量线段BF=cm ．

查看试题解析
24. 已知：如图，AB $//$ CD ， BE交CD于点M ， ∠B=∠D ．
求证：BE $//$ DF ．

查看试题解析
25. 应用题：
为了丰富学生校园生活，满足学生的多元文化需求，促进学生身心健康和谐发展，学校将要举行趣味运动会，体育组准备购买跳绳作为奖品．已知1条短跳绳和3条长跳绳，共需要96元；2条短跳绳和1条长跳绳共需要62元．

(1)、求每条短跳绳和每条长跳绳各多少元；

(2)、商店举行“优惠促销”活动，具体办法如下：短跳绳“九折”优惠；长跳绳不超过10条不优惠，超出10条的部分“六折”优惠．如果买m条短跳绳需要y₁元，买n条长跳绳需要y₂元．请用含m ， n的代数式分别表示y₁和y₂；

(3)、如果在（2）的条件下，购买同一种奖品50件，请分析买哪种奖品省钱．

查看试题解析

26. 阅读材料：

延庆区某校七年级共10个班，综合实践小组的同学对本校七年级学生课外阅读最喜爱的图书种类进行了调查．围绕着“你最喜欢的是哪一类课外书？（只写一项）”的问题，对该校七年级学生进行了随机抽样调查．

收集数据

A ．文学类 B ．艺体类 C ．科普类 D ．其他

通过调查得到的一组数据如下：

A C C A D A B A C B B A D C A A B C C A

A C B D A A B D A A B B C C A C A C D A

B D B C A D A D C A A C B D A A D C A A

B B C C D C A A B A A C C A D A B A A B

整理、描述数据

综合实践小组的同学对抽样调查的数据进行整理，绘制了如下统计图表（不完整）：

类别	频数
A ．文学类	32
B ．艺体类	a
C ．科普类	20
D ．其他	b
总计	80

根据以上信息，回答下列问题：

①表1中的a = ，b = ；

②请将图1补充完整；

③图2中，，“文学类”部分扇形的圆心角是 $°$ ；

④若该校七年级共有学生360人，根据调查结果估计七年级最喜欢“科普类”图书的学生约有人．

查看试题解析

27. 在三角形ABC中，点D在线段AC上，ED $//$ BC交AB于点E ，点F在线段AB上（点F不与点A ， E ， B重合），连接DF ，过点F作FG⊥FD交射线CB于点G ．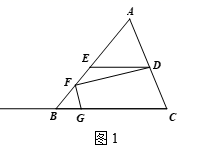

(1)、如图1，点F在线段BE上，用等式表示∠EDF与∠BGF的数量关系，并证明；

(2)、如图2，点F在线段BE上，求证：∠ABC+∠BFG－∠EDF=90°；

(3)、当点F在线段AE上时，依题意，在图3中补全图形，请直接用等式表示∠EDF与∠BGF的数量关系，不需证明．

查看试题解析
28. 对于有理数a ， b ，定义 $\max {a ， b}$ 的含义为：当a≥b时， $\max {a ， b}$ ＝a；当a＜b时， $\max {a ， b}$ ＝b ．例如：max{1，－2}＝1，max{－3，－3}＝－3，max{－1，0}＝0．

(1)、max{－6，6}=；

(2)、max{－x²＋1，2}=；

(3)、已知max{－2k＋5，－1}＝－2k＋5，求k的取值范围；

(4)、已知max{2x－3，－2x－1}=9，求x的值；

(5)、已知max{－20，m²+n²－8m+4n}＝－20，直接写出m ， n的值．

查看试题解析