13.2.1 作轴对称图形 同步练习----初中数学人教版八年级上册
试卷更新日期:2021-08-10 类型:同步测试
一、单选题
-
1. 如图,在 正方形网格中,已将图中的四个小正方形涂上阴影,若再从图中选一个涂上阴影,使得整个阴影部分组成的图形是轴对称图形,那么不符合条件的小正方形是( )
 A、① B、② C、③ D、④
A、① B、② C、③ D、④ -
2. 下面是四位同学所作的 关于直线 对称的图形,其中正确的是( )A、
 B、
B、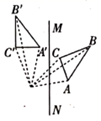 C、
C、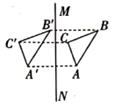 D、
D、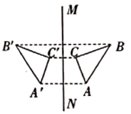
-
3. 如图,是一个三角板,则下列选项中可能是由该图经过一次轴对称变换后得到的是( )
 A、
A、 B、
B、 C、
C、 D、
D、
-
4. 如图,在3×3的正方形的网格中,格线的交点称为格点,以格点为顶点的三角形称为格点三角形,图中的△ABC为格点三角形,在图中最多能画出( )个格点三角形与△ABC成轴对称.
 A、6个 B、5个 C、4个 D、3个
A、6个 B、5个 C、4个 D、3个 -
5. 如图是跳棋盘,其中格点上的黑色点为棋子,剩余的格点上没有棋子.我们约定跳棋游戏的规则是:把跳棋棋子在棋盘内沿直线隔着棋子对称跳行,跳行一次称为一步.已知点A为已方一枚棋子,欲将棋子A跳进对方区域(阴影部分的格点),则跳行的最少步数为( )
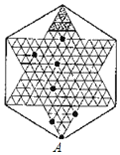 A、2 步 B、3 步 C、4 步 D、5 步
A、2 步 B、3 步 C、4 步 D、5 步 -
6. 小军同学在网格纸上将某些图形进行平移操作,他发现平移前后的两个图形所组成的图形可以是轴对称图形.如图所示,现在他将正方形 从当前位置开始进行一次平移操作,平移后的正方形的顶点也在格点上,则使平移前后的两个正方形组成轴对称图形的平移方向有( )
 A、3个 B、4个 C、5个 D、无数个
A、3个 B、4个 C、5个 D、无数个 -
7. 如图是一个经过改造的台球桌面的示意图,图中四个角上的阴影部分分别表示四个入球孔.如果一个球按图中所示的方向被击出(球可以经过多次反射),那么该球最后将落入的球袋是( )
 A、1号袋 B、2号袋 C、3号袋 D、4号袋
A、1号袋 B、2号袋 C、3号袋 D、4号袋 -
8. 把一张正方形纸片按如图所示的方法对折两次后剪去两个角,那么打开以后的形状是( )
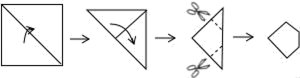 A、六边形 B、八边形 C、十二边形 D、十六边形
A、六边形 B、八边形 C、十二边形 D、十六边形 -
9. 如图所示,将矩形纸片先沿虚线AB按箭头方向向右对折,接着对折后的纸片沿虚线CD向下对折,然后剪下一个小三角形,再将纸片打开,则打开后的展开图是( )
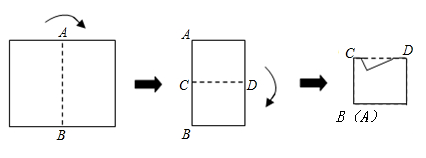 A、
A、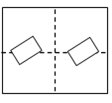 B、
B、 C、
C、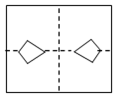 D、
D、
二、填空题
-
10. 求作与已知图形成轴对称的图形,先观察图形,并确定能代表已知图形的关键点,分别作出这些关键点关于对称轴的 , 根据已知图形连接这些对应点,即可得到与已知图形成轴对称的图形.
-
11. 如图,某英语单词由四个字母组成,且四个字母都关于直线l对称,则这个英语单词的汉语意思为 .

-
12. 如图,是4×4正方形网格,其中已有三个小方格涂成黑色,在剩下的13个白色小方格中随意选一个涂成黑色,使得黑色小方格组成的图形为轴对称图形的涂法有种

-
13. 如图,在 的正方形的网格中,格线的交点称为格点,以格点为顶点的三角形称为格点三角形.图中的 为格点三角形,在图中最多能画出个不同的格点三角形与 成轴对称.

-
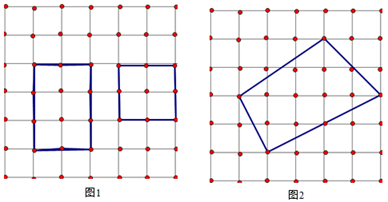
14. “皮克定理”是用来计算顶点在格点(即图中虚线的交点,如图中的小黑点)上的多边形的面积公式,公式为S = a + -1.小明只记得公式中的表示多边形的面积,a 和 b 中有一个表示多边形边上(含多边形顶点)的格点个数,另一个表示多边形内部的格点个数,但记不清楚究竟是哪一个表示多边形内部的格点个数,请你利用图 1 探究并运用探究的结果求图 2 中多边形的面积是.
三、解答题
-
15. 如图是4×4正方形网格,其中已有3个小方格涂成了黑色.现在要从其余13个白色小方格中选出一个也涂成黑色,使整个涂成黑色的图形成为轴对称图形,这样的白色小方格有多少个?请分别在下图中涂出来,并画出这个轴对称图形的对称轴.


四、综合题
-
16. 如图所示,在正方形网格中,每个小正方形的边长为1个单位.
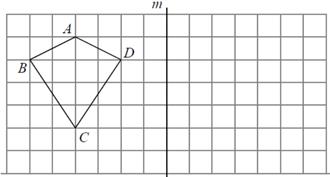 (1)、过直线m作四边形 的对称图形;(2)、求四边形 的面积.
(1)、过直线m作四边形 的对称图形;(2)、求四边形 的面积.
