重庆市开州区2020-2021学年八年级下学期数学期末考试试卷

试卷更新日期：2021-08-10 类型：期末考试

进入出卷网下载

一、单选题

1. 下列二次根式中，属于最简二次根式的是（）

A、 $\sqrt{\frac{1}{3}}$ B、 $\sqrt{0.3}$ C、 $\sqrt{3}$ D、 $\sqrt{20}$

查看试题解析
2. 下列各组数中，不是勾股数的是（　　）

A、5，12，13 B、8，15，17 C、3，4，5 D、13，14，15

查看试题解析
3. 已知在平行四边形ABCD中，∠A＝∠B+40°，则∠A的度数为（）

A、35° B、70° C、110° D、140°

查看试题解析
4. 在一次射击训练中，甲、乙两人各射击了10次，两人10次射击成绩的平均数都是9.1环，方差分别是S_甲²＝1.3，S_乙²＝1.7，则关于甲、乙两人在这次射击训练中成绩稳定的描述正确的是（）

A、甲比乙稳定 B、乙比甲稳定 C、甲和乙一样稳定 D、甲、乙稳定性没法对比

查看试题解析
5. 下列4个命题：
①对角线相等且互相平分的四边形是正方形；②有三个角是直角的四边形是矩形；③对角线互相垂直的平行四边形是菱形；④一组对边平行，另一组对边相等的四边形是平行四边形其中正确的是（）

A、②③ B、② C、①②④ D、③④

查看试题解析
6. 估计 $\sqrt{3}$ （ $\sqrt{6}$ ﹣ $\sqrt{3}$ ）的值应在（）

A、0和1之间 B、1和2之间 C、2和3之间 D、3和4之间

查看试题解析
7. 如图，在矩形ABCD中，点E，F分别在边BC和AD上，把该矩形沿EF折叠，使点B恰好落在边AD的点H处，∠CEH＝60°，已知矩形ABCD的面积为36 $\sqrt{3}$ ，FH＝2HD，则折痕EF的长为（）

A、3 B、3 $\sqrt{3}$ C、6 D、6 $\sqrt{3}$

查看试题解析
8. 若数a使关于x的不等式组 ${\begin{array}{l} 3 - 2 x \geq a - 2 (3 x - 1) \\ 2 - x \geq \frac{1 - x}{2} \end{array}$ 恰有3个整数解，且使关于y的分式方程 $\frac{2}{y - 1} + \frac{a}{1 - y}$ ＝3的解为整数，则符合条件的所有整数a的和为（）

A、10 B、7 C、5 D、2

查看试题解析

二、填空题

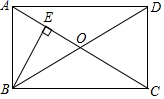
9. 一组数据是4，6，7，10，11共五个数，则这组数据的中位数是 .

查看试题解析
10. 环境空气质量问题已经成为人们日常生活所关心的重要问题，我国新修订的《环境空气质量标准》中增加了 $P M 2.5$ 检测指标，“ $P M 2.5$ ”是指大气中危害健康的直径小于或等于2.5微米的颗粒物，2.5微米即0.0000025米.用科学记数法表示0.0000025为.

查看试题解析
11. 将直线y=2x-3向上平移2个单位后的直线解析式是.

查看试题解析
12. 如图，矩形ABCD中，BE⊥AC于点E，若∠ACB＝35°，则∠DBE＝度.

查看试题解析
13. 某公司以A、B两种材料，利用不同的搭配方式推出了两款产品，其中，甲产品每份含200克A、200克B；乙产品每份含200克A、100克B，甲乙两种产品每份成本价分别为A、B两种材料的成本之和，若甲产品每份成本为16元，公司在核算成本的时候把A、B两种材料单价看反了，实际成本比核算时的成本多760元，如果每天甲销量的4倍和乙销量的3倍之和不超过120份，那么公司每天的实际成本最多为元.

查看试题解析

三、解答题

14. 计算： ${(2 + \sqrt{3})}^{0} + {(- 1)}^{2021} - | \sqrt{8} - 1 |$ .

查看试题解析
15. 如图，直线AB∥CD，点E在CD上，点O、点F在AB上，连接OE，过点F作FH⊥OE于点H.

(1)、尺规作图：作∠EOF的角平分线OG交CD于点G；（不写作法，保留作图痕迹，并标明字母）

(2)、在（1）的条件下，已知∠OFH＝20°，求∠OGD的度数.

查看试题解析
16. 近日，我区中小学防溺水安全教育正式启动，某校积极响应并开展“防溺水安全知识竞赛”活动，从八年级、九年级各随机抽取10名学生的竞赛成绩进行统计整理如下：
九年级抽取的学生竞赛成绩：85，65，80，90，80，90，90，50，100，90.

八年级、九年级抽取的学生竞赛成绩统计表

年级

平均数

众数

中位数

八年级

81

70

80

九年级

82

a

b

根据以上信息，解答下列问题：

(1)、表中a＝， b＝；

(2)、根据上述数据，你认为该校八、九年级中哪个年级学生掌握防溺水安全知识较好？请说明理由（一条理由即可）；

(3)、该校八年级的600名学生和九年级的700名学生参加了此次竞赛活动，请估计这两个年级竞赛成绩达到90分及以上的学生人数是多少？

查看试题解析
17. 如图，△ABC中，AB＝BC，BE⊥AC于点E，AD⊥BC于点D，∠BAD＝45°，AD与BE交于点F，连接CF.

(1)、求证：BF＝2AE；

(2)、若CD＝3，求AD的长.

查看试题解析
18. 小明同学根据函数的学习经验，对函数y＝|x﹣2|+|x+4|进行了探究，下面是他的探究过程：

(1)、已知当x＝﹣4时，|x+4|＝0；当x＝2时，|x﹣2|＝0，化简：
①当x＜﹣4时，y＝；

②当﹣4≤x≤2时，y＝；

③当x＞2时，y＝.

(2)、在平面直角坐标系中画出y＝|x﹣2|+|x+4|的图象，根据图象写出该函数的一条性质： ▲ .

(3)、根据上面的探究解决下面问题：
已知P（a，0）是x轴上一动点，A（﹣4，6），B（2，6），则AP+BP的最小值是 .

查看试题解析
19. 从三位数m的各数位上的数字中任选两个构成一个两位数，这样就可以得到六个两位数，我们把这六个两位数叫做数m的“生成数”.数m的“生成数”之和与22的商记为G（m），例如m＝123，G（123）＝ $\frac{12 + 13 + 21 + 23 + 31 + 32}{22}$ ＝6.

(1)、直接写出G（234）＝ ▲ ；并证明：对于任意的三位数n，G（n）为整数；

(2)、数p，q是两个三位数，他们都有“生成数”，p＝100a+40+b（1≤a≤9，1≤b≤9且a≠b），q＝130+c（1≤c≤3），规定：k＝ $\frac{p}{q}$ ，若G（p）•G（q）＝56，求k的最大值.

查看试题解析
20. 已知：如图四边形ABCD是正方形，∠EAF＝45°.

(1)、如图1，若点E，F分别在边BC、CD上，延长线段CB至G，使得BG＝DF，若BE＝4，BG＝3，求EF的长；

(2)、如图2，若点E，F分别在边CB、DC延长线上时，求证：EF＝DF﹣BE；

(3)、如图3，如果四边形ABCD不是正方形，但满足AB＝AD，∠BAD＝∠BCD＝90°，∠EAF＝45°，且BC＝8，DC＝12，CF＝6，请你直接写出BE的长.

查看试题解析

年级	平均数	众数	中位数
八年级	81	70	80
九年级	82	a	b