重庆市南川区2020-2021学年八年级下学期数学期末考试试卷
试卷更新日期:2021-08-10 类型:期末考试
一、单选题
-
1. 二次根式 有意义,则实数x的取值范围是( )A、x>2 B、x≥2 C、x≥﹣2 D、x≤﹣22. 正比例函数y=3x的图象必经过点( )A、(﹣1,﹣3) B、(﹣1,3) C、(1,﹣3) D、(3,1)3. 下列各曲线中不能表示y是x的函数的是( )A、
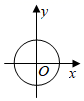 B、
B、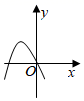 C、
C、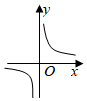 D、
D、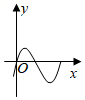 4. 若甲、乙、丙、丁四人参加跳远比赛,经过几轮初赛,他们的平均成绩相同,方差分别是:S =0.34,S =0.21,S =0.4,S =0.45.你认为最应该派去的是( )A、甲 B、乙 C、丙 D、丁5. 下列四个选项中,不符合直线y=x﹣2的性质特征的选项是( )A、经过第一、三、四象限 B、y随x的增大而增大 C、与x轴交于(﹣2,0) D、与y轴交于(0,-2)6. 如图,小红在作线段AB的垂直平分线时,操作如下:分别以点A、B为圆心,大于AB的长为半径、在线段AB的两侧画弧,两弧分别相交于点C、D,则直线CD即为所求,连接AC、BC、AD、BD,根据她的作法可知四边形ADBC一定是( )
4. 若甲、乙、丙、丁四人参加跳远比赛,经过几轮初赛,他们的平均成绩相同,方差分别是:S =0.34,S =0.21,S =0.4,S =0.45.你认为最应该派去的是( )A、甲 B、乙 C、丙 D、丁5. 下列四个选项中,不符合直线y=x﹣2的性质特征的选项是( )A、经过第一、三、四象限 B、y随x的增大而增大 C、与x轴交于(﹣2,0) D、与y轴交于(0,-2)6. 如图,小红在作线段AB的垂直平分线时,操作如下:分别以点A、B为圆心,大于AB的长为半径、在线段AB的两侧画弧,两弧分别相交于点C、D,则直线CD即为所求,连接AC、BC、AD、BD,根据她的作法可知四边形ADBC一定是( ) A、菱形 B、矩形 C、正方形 D、梯形7. 放学以后,红红和晓晓从学校分手,分别沿东南方向和西南方向回家,若红红和晓晓行走的速度都是50米/分,红红用12分钟到家,晓晓用16分钟到家,红红家和晓晓家的直线距离为( )A、600米 B、800米 C、1000米 D、不能确定8. 如图,将一个矩形纸片ABCD折叠,使C点与A点重合.折痕为EF.若AB=8,BC=16,则BE的长是( )
A、菱形 B、矩形 C、正方形 D、梯形7. 放学以后,红红和晓晓从学校分手,分别沿东南方向和西南方向回家,若红红和晓晓行走的速度都是50米/分,红红用12分钟到家,晓晓用16分钟到家,红红家和晓晓家的直线距离为( )A、600米 B、800米 C、1000米 D、不能确定8. 如图,将一个矩形纸片ABCD折叠,使C点与A点重合.折痕为EF.若AB=8,BC=16,则BE的长是( ) A、12 B、10 C、8 D、69. 如图,已知四边形ABCD是平行四边形,下列结论中正确的是( )
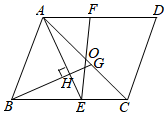
A、12 B、10 C、8 D、69. 如图,已知四边形ABCD是平行四边形,下列结论中正确的是( )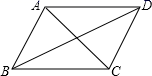 A、当AC=BD时,它是正方形 B、当AC⊥BD时,它是矩形 C、当∠ABC=90°时,它是菱形 D、当AB=BC时,它是菱形10. 如图,正方形ABCD的边长为4.对角线AC,BD交于点O,E是AC延长线上一点,且CE=CO.则BE的长度为( )
A、当AC=BD时,它是正方形 B、当AC⊥BD时,它是矩形 C、当∠ABC=90°时,它是菱形 D、当AB=BC时,它是菱形10. 如图,正方形ABCD的边长为4.对角线AC,BD交于点O,E是AC延长线上一点,且CE=CO.则BE的长度为( ) A、4 B、6 C、2 D、411. 如图,A.B两地之间的路程为6000米,甲、乙两人骑车都从A地出发,已知甲先出发5分钟后,乙才出发,乙在A、B之间的C地追赶上甲,当乙追赶上甲后,乙立即返回A地,甲继续往B地前行.甲到达B地后停止骑行,乙骑行到达A地时也停止(乙在C地掉头时间忽略不计).在整个骑行过程中,甲和乙都保持各自速度匀速骑行,甲乙两人相距的路程y(米)与甲出发的时间x(分钟)之间的关系如图所示.下列说法正确的是( )
A、4 B、6 C、2 D、411. 如图,A.B两地之间的路程为6000米,甲、乙两人骑车都从A地出发,已知甲先出发5分钟后,乙才出发,乙在A、B之间的C地追赶上甲,当乙追赶上甲后,乙立即返回A地,甲继续往B地前行.甲到达B地后停止骑行,乙骑行到达A地时也停止(乙在C地掉头时间忽略不计).在整个骑行过程中,甲和乙都保持各自速度匀速骑行,甲乙两人相距的路程y(米)与甲出发的时间x(分钟)之间的关系如图所示.下列说法正确的是( )①乙的速度为227.5米/分;②甲的速度为150米/分;③图中M点的坐标为(21,2940);④乙到达A地时,甲与B地相距3060米.( )
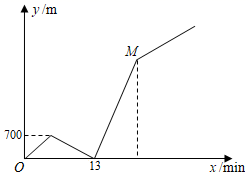 A、①②③ B、②③④ C、①③④ D、①②④12. 已知整数a.使得关于x的分式方程 +3= 有整数解.且关于x的一次函数y=(a﹣1)x+6﹣a的图象不经过第四象限,则所有满足条件的整数a的值的和是( )A、10 B、14 C、16 D、24
A、①②③ B、②③④ C、①③④ D、①②④12. 已知整数a.使得关于x的分式方程 +3= 有整数解.且关于x的一次函数y=(a﹣1)x+6﹣a的图象不经过第四象限,则所有满足条件的整数a的值的和是( )A、10 B、14 C、16 D、24二、填空题
-
13. 计算:()2=14. 如图,在△ABC中,点D、E分别是AB、AC边的中点,若BC=6cm.则线段DE=cm.
 15. 矩形两条对角线的夹角为60°,对角线长为14,则该矩形较短边的边长为.16. 若点A(x1 , y1)和点B(x1+1,y2)都在一次函数y=2021x﹣2020的图象上,则y1y2(选择“>”、“<“或“=”填空).17. 如图,在Rt△ABC中,∠BCA=90°.BC=5.AC=10,E为斜边AB边上的一动点,以EA、EC为边作平行四边形,则线段ED长度的最小值为.
15. 矩形两条对角线的夹角为60°,对角线长为14,则该矩形较短边的边长为.16. 若点A(x1 , y1)和点B(x1+1,y2)都在一次函数y=2021x﹣2020的图象上,则y1y2(选择“>”、“<“或“=”填空).17. 如图,在Rt△ABC中,∠BCA=90°.BC=5.AC=10,E为斜边AB边上的一动点,以EA、EC为边作平行四边形,则线段ED长度的最小值为. 18. 为了改善城市绿化,南川区政府决定圈出一块地打造一片花园,花园中种植牡丹花、樱花、梅花供市民欣赏,经过一段时间,花园中已种植的牡丹花、樱花、梅花的面积之比为5:4:6,根据市民喜爱程度,将在花园余下空地继续种植这三种花,经过测算,需将余下空地面积的 种植梅花,则梅花种植的总面积将达到这三种花种植总面积的 ,为了使牡丹花种植总面积与樱花种植总面积之比达到4:5,则花园内种植樱花的总面积与种植梅花的总面积之比 .
18. 为了改善城市绿化,南川区政府决定圈出一块地打造一片花园,花园中种植牡丹花、樱花、梅花供市民欣赏,经过一段时间,花园中已种植的牡丹花、樱花、梅花的面积之比为5:4:6,根据市民喜爱程度,将在花园余下空地继续种植这三种花,经过测算,需将余下空地面积的 种植梅花,则梅花种植的总面积将达到这三种花种植总面积的 ,为了使牡丹花种植总面积与樱花种植总面积之比达到4:5,则花园内种植樱花的总面积与种植梅花的总面积之比 .三、解答题
-
19. 计算:(1)、(4+ )(4﹣ );(2)、 ﹣ × .20. 如图,在平行四边形ABCD中,∠C=50°.
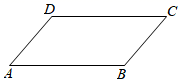 (1)、作∠BAD的平分线AE交DC于E; (尺规作图,不写作法,保留作图痕迹,并标明字母).(2)、按(1)作图所示,若BC=7,AB=11,求CE的长.21. 某中学在全校七、八年级共800名学生中开展“国家安全法”知识竞赛,并从七、八年级学生中各抽取20名学生,统计这部分学生的竞赛成绩(竞赛成绩均为整数,满分10分,6分及以上为合格).相关数据整理如下:
(1)、作∠BAD的平分线AE交DC于E; (尺规作图,不写作法,保留作图痕迹,并标明字母).(2)、按(1)作图所示,若BC=7,AB=11,求CE的长.21. 某中学在全校七、八年级共800名学生中开展“国家安全法”知识竞赛,并从七、八年级学生中各抽取20名学生,统计这部分学生的竞赛成绩(竞赛成绩均为整数,满分10分,6分及以上为合格).相关数据整理如下:八年级抽取的学生的竞赛成绩:4,4,6,6,6,6,7,7,7,8,8,8,8,8,8,9,9,9,10,10.
七,八年级抽取的学生的竞赛成绩统计表
年级
七年级
八年级
平均数
7.4
7.4
中位数
a
b
众数
7
c
合格率
85%
90%
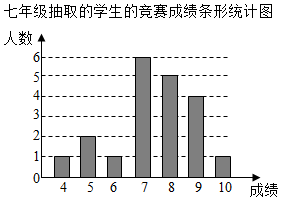
根据以上值息,解答下列问题:
(1)、填空a=;b=;c=.(2)、估计该校七、八年级共800名学生中竞赛成绩达到9分及以上的人数;(3)、根据以上数据分析,从一个方面评价两个年级“国家安全法”知识竞赛的学生整体成绩谁更优异.22. 已知:一次函数y=kx+b的图象经过M(0,6),N(﹣2,2)两点.(1)、求一次函数的解析式;(2)、若点P(a﹣5,3a)在该函数图象上,求点P的坐标.23. 山王坪的门票销售分两类:一类为散客门票,价格50元/张,另一类为团体门票(一次性购买门票10张及以上),每张门票价格在散客价格基础上打8折.某班部分同学要去山王坪旅游,设参加旅游x人,购买门票需要y元.(1)、求y与x之间的函数解析式,并写出自变量的取值范围.(2)、请根据人数变化设计一种比较省钱的购票方案.24. 阅读理解:若x满足(30﹣x)(x﹣10)=160,求(30﹣x )2+(x﹣10)2的值.解:设30﹣x=a,x﹣10=b,
则(30﹣x)(x﹣10)=ab=160,a+b=(30﹣x)+(x﹣10)=20,(30﹣x)2+(x﹣10)2=a2+b2=(a+b)2﹣2ab=202﹣2×160=80
解决问题:
(1)、若x满足(2020﹣x)(x﹣2016)=4.求(2020﹣x) 2+(x﹣2016)2的值;(2)、如图,在矩形ABCD中,AB=20,BC=12,点E、F是BC、CD上的点,且BE=DF=x.分别以FC、CE为边在矩形ABCD外侧作正方形CFGH和CEMN,若矩形CEPF的面积为160平方单位,求图中阴影部分的面积和.