重庆市潼南区2020-2021学年八年级下学期数学期末考试试卷
试卷更新日期:2021-08-10 类型:期末考试
一、单选题
-
1. 若 在实数范围内有意义,则x的取值范围是( )A、 B、 C、 D、
-
2. 以下各组数为三角形的三边长(单位均为米),其中能够构成直角三角形的是( )A、1,2,3 B、8,13,15 C、5,12,13 D、10,15,20
-
3. 下列不能判定一个四边形是平行四边形的是( )A、两组对边分别平行的四边形是平行四边形 B、两组对边分别相等的四边形是平行四边形 C、一组对边平行另一组对边相等的四边形是平行四边形 D、对角线互相平分的四边形是平行四边形
-
4. 某服装销售商在进行市场占有率的调查时,他最应该关注的是( )
A、服装型号的平均数 B、服装型号的众数 C、服装型号的中位数 D、最小的服装型号 -
5. 在直角坐标系中与 在同一个正比例函数图象上的是( )A、 B、 C、 D、
-
6. 数学老师在课堂上给同学们布置了10个填空题作为课堂练习,并将全班同学的答题情况绘制成条形统计图.由图可知,全班同学答对题数的中位数为( )
 A、7 B、8 C、8.5 D、9
A、7 B、8 C、8.5 D、9 -
7. 估计 的值应在( )A、5和6之间 B、6和7之间 C、7和8之间 D、9和10之间
-
8. 如图,在正方形 中,E为对角线 上一点,连接 、 , ,则 为( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
9. 周末小丽从家里出发骑单车去公园,因为她家与公园之间是一条笔直的自行车道,所以小丽骑得特别放松.途中,她在路边的便利店挑选一瓶矿泉水,耽误了一段时间后继续骑行,愉快地到了公园.图中描述了小丽路上的情景,下列说法中错误的是( )
 A、小丽在便利店时间为15分钟 B、公园离小丽家的距离为2000米 C、小丽从家到达公园共用时间20分钟 D、小丽从家到便利店的平均速度为100米/分钟
A、小丽在便利店时间为15分钟 B、公园离小丽家的距离为2000米 C、小丽从家到达公园共用时间20分钟 D、小丽从家到便利店的平均速度为100米/分钟 -
10. 已知,如图,正方形 的面积为25,菱形 的面积为20,求阴影部分的面积( )
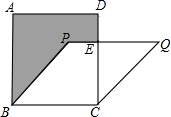 A、11 B、6.5 C、7 D、7.5
A、11 B、6.5 C、7 D、7.5 -
11. 如果关于 的分式方程 有非负整数解,且一次函数 不经过四象限,则所有符合条件的 的和是( ).A、0 B、2 C、3 D、5
-
12. 如图,在正方形 中, 、 分别为 、 上的点,且 平分 , , 为线段 上的动点,记 的最小值为 ,若正方形边长为 ,则 的值为( )
 A、 B、 C、 D、
A、 B、 C、 D、
二、填空题
-
13. 计算: .
-
14. 将直线 向下平移1个单位后得到的直线解析式为
-
15. 一个三角形的三边的比为5∶12∶13,它的周长为60cm,则它的面积是 .
-
16. 平行四边形的一个内角平分线将该平行四边形的一边分为2cm和3cm两部分,则该平行四边形的周长为 .
-
17. 如图,对折矩形纸片 ,使 与 重合,得到折痕 ,把纸片展平后再次折叠,使点A落在折痕 上的点 处,得到折痕 .若直线 交直线 于点H, , , 的长为

-
18. 采购员用一张1万元支票去购物,购单价为590元的A种物品若干件,又购单价为670元的B种物品若干件,其中B种件数多于A种件数,找回了几张100元和几张10元的(10元的不超过9张).如把购A种物品和B种物品的件数互换,找回的100元和10元的钞票张数也恰好相反,则原来购B种物品件.
三、解答题
-
19. 计算:
① ;
②
-
20. 如图,已知在四边形 中, ,连接 、 .
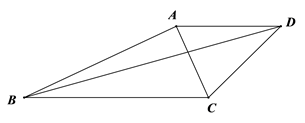 (1)、用基本尺规作图:作 的角平分线 ,交 的延长线于点 ,交 于 (保留画图的痕迹,不写作法);(2)、若 是 的中点, , ,求 的长.
(1)、用基本尺规作图:作 的角平分线 ,交 的延长线于点 ,交 于 (保留画图的痕迹,不写作法);(2)、若 是 的中点, , ,求 的长. -
21. “无篮球,不青春”,2018年来,潼南区举办了系列篮球赛活动,展现了全区人民积极向上的青春风采,为加强教师们的联系,提高教师的身体素质,某校也积极响应区体委的倡导,在本校内开展一系列篮球比赛,在活动收尾阶段,举办了“各年级组间的教师友谊赛”,在女教师的比赛环节中,初一,初二两个年级组各随机派出10名女教师定点投篮10次,进球个数(x)作为这名女教师的成绩,学校对数据进行整理,将数据分为5组:(A组: ;B组: ;C组: ;D组: :E组: )通过分析后,得到如下部分信息:
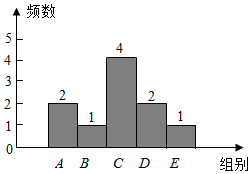
A.初一年级组参赛女教师定点投篮投球成绩频数分布直方图
B.初一年级组参赛女教师定点投篮投球个数在C组 这一组的数据是:5、5、5、6
C.初二年级组参赛女教师定点投篮投球成绩统计表
参赛教师编号
1
2
3
4
5
6
7
8
9
10
投中球数
8
3
4
5
4
10
3
6
4
7
D.初一、初二参赛女教师定点投篮投球个数的平均数、中位数、众数如下:
年级
平均数
中位数
众数
初一
5.4
n
5
初二
m
4.5
t
根据以上信息,解答下列问题:
(1)、填空: , , .(2)、根据以上数据分析,你认为初一、初二哪支队伍“定点投篮”成绩更优异,请说明理由(写出一条理由即可);(3)、若我区女教师共有3200名,估计全区女教师“定点投篮”进球个数不少于5个的人数. -
22. 学习一次函数时,我们通过列表、描点、连线画出一次函数图象,并结合函数图象研究函数性质.小双结合学习一次函数的经验,对函数 的图象和性质进行了研究,下面是小双的探讨过程,请补充完整:
 (1)、化简:当 时, :当 时,
(1)、化简:当 时, :当 时,列表:
x
…
-2
-1
0
1
2
3
…
y
…
m
1
2
3
2
n
…
其中, ; ;
(2)、描点、连线;①在图中画出该函数图象;
②结合图象,写出该函数的一条性质: ▲ ;
(3)、过点 作直线 轴,结合所画的函数图象,当a的取值范围在时,直线 与函数 图象有两个交点. -
23. 洪水无情,人有情,依靠政府战灾情.2020特大洪水虽然给我区人民造成极大损失,但全区人民在区政府的领导之下,老百姓相互支持,很快恢复生产,并喜获丰收2020年下半年,桂林坝某农户种植基地收获萝卜192吨,准备运给甲、乙两地的承包商进行包销.该基地用大、小两种货车共18辆恰好能一次性运完这批萝卜,已知这两种货车的载重量分别为14吨/辆和8吨/辆,运往甲、乙两地的运费如下表:
车型
运费
运往甲地/(元/辆)
运往乙地/(元/辆)
大货车
720
800
小货车
500
650
(1)、求这两种货车各用多少辆;(2)、如果安排10辆货车前往甲地,其余货车前往乙地,其中前往甲地的大货车为a辆,总运费为w元,求w关于a的函数关系式;(3)、在(2)的条件下,若甲地的承包商包销的萝卜不少于96吨,请你设计出使总运费最低的货车调配方案,并求出最低总运费. -
24. 材料一:若一个四位数千位、百位、十位、个位上的数字分别为a、b、c、d,则这个四位数可以表示为 .
材料二:若一个四位数 满足 ,我们就称这个四位数是平方和数,如对于四位数6453,∵ ,∴6453是平方和数,当然3456也是平方和数.
请根据以上信息完成下面问题:
(1)、判断2457,5414是否为平方和数,并说明理由;(2)、若四位数 是平方和数,请求出这个数. -
25. 如图1和图2,矩形 中,E是 的中点,P是 上一点, , .
 (1)、作射线 交直线 于点G,如图1.
(1)、作射线 交直线 于点G,如图1.①求证: ;
②若点F在 下方, , ,求 的长.
(2)、若点F在 上方,如图2,写出 , , 的等量关系,并证明你的结论. -
26. 如图,在平面直角坐标系中,直线 分别与x轴、y轴交于点B、C,且与直线 交于点A.
 (1)、分别求出点A、B、C的坐标;(2)、若D是线段OA上的点,且△COD的面积为12,求直线CD的函数表达式;
(1)、分别求出点A、B、C的坐标;(2)、若D是线段OA上的点,且△COD的面积为12,求直线CD的函数表达式;
(3)、在(2)的条件下,设P是射线CD上的点,在平面内是否存在点Q,使以O、C、P、Q为顶点的四边形是菱形?若存在,直接写出点Q的坐标;若不存在,请说明理由.
