湖南省怀化市部分县区2020-2021学年八年级下学期数学期末考试试卷

试卷更新日期：2021-08-10 类型：期末考试

进入出卷网下载

一、多选题

1. 下列数组中，不是勾股数的一组是（）

A、3，4，5 B、1， $\sqrt{2}$ ， $\sqrt{3}$ C、6、8、10 D、2、3、5

查看试题解析

二、单选题

2. 如图，CD是△ABC的边AB上的中线，且CD＝ $\frac{1}{2}$ AB，则下列结论错误的是（）

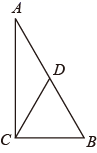A、AD＝BD B、∠A＝30° C、∠ACB＝90° D、△ADC与△BCD的面积相等

查看试题解析
3. 一个正多边形的内角和为540°，则这个正多边形的每一个外角等于（　　）

A、108° B、90° C、72° D、60°

查看试题解析
4. 下列图形中是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
5. 如图，在▱ABCD中，AB=6cm，BC=10cm，AC=8cm，BD=14cm，则下列结论中：①△AOB的周长是17cm，②△ACD是直角三角形，③AD=14cm，④▱ABCD的面积是48cm² ，其中正确有（）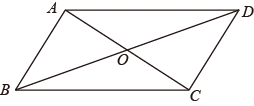

A、1个 B、2个 C、3个 D、4个

查看试题解析
6. 如点 $A (- a ， a - 2)$ 在第二象限，那么 $a$ 的值可能是（）

A、0 B、1 C、2 D、3

查看试题解析
7. 若点A（2，4）在函数 $y = k x - 2$ 的图象上，则下列各点在此函数图象上的是（）.

A、（0， $- 2$ ） B、（ $\frac{3}{2}$ ，0） C、（8，20） D、（ $\frac{1}{2}$ ， $\frac{1}{2}$ ）

查看试题解析
8. 如图，四边形ABCD的对角线AC、BD相交于O，下列判断正确的是（）

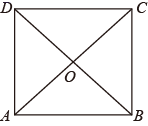A、若AC⊥BD，则四边形ABCD是菱形 B、若AC＝BD，则四边形ABCD是矩形 C、若AB=DC，AD∥BC，则四边形ABCD是平行四边形 D、若AO=OC，BO=OD，则四边形ABCD是平行四边形

查看试题解析
9. 已知直线y＝2x﹣4，则它与两坐标轴围成的三角形的面积是（）

A、2 B、3 C、4 D、5

查看试题解析

三、填空题

10. 已知点A（ $- 3$ ， $a$ ）与点B（ $- 3$ ， $- 4$ ）关于 $x$ 轴对称，则 $a$ =.

查看试题解析
11. 一次函数 $y = - \frac{1}{2} x + 1$ 的图象不经过第象限.

查看试题解析
12. 如图，在菱形ABCD中，E，F分别是AD，BD的中点，若EF=2，则菱形ABCD的周长是.

查看试题解析

13. 某同学做掷硬币试验，正面朝上记为“正”，反面朝上记为“反”，结果统计如下：

次数	1	2	3	4	5	6	7	8	9	10
结果	反	正	正	反	正	正	反	正	正	反

则“正面朝上”的频数是；“反面朝上”的频率是.

查看试题解析

14. 如图，一次函数 $y = k x + b$ 的图象与坐标轴的交点坐标分别为A（0，2），B（-3，0），下列说法：① $y$ 随 $x$ 的增大而减小；② $b = - 3$ ；③关于 $x$ 的方程 $k x + b = 0$ 的解为 $x = 2$ ；④关于 $x$ 的不等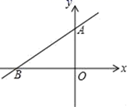式 $k x + b < 0$ 的解集 $x < - 3$ .其中说法正确的有.

查看试题解析
15. 如图，某校的生物园形状是一个直角三角形， $∠ A C B = 90 °$ ，AC=40m，BC=30m.现要修建一条水渠CD， $D$ 点在边 $A B$ 上，若水渠的造价为800元 $/ m$ ，则修建水渠CD最少要元.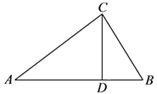

查看试题解析

四、解答题

16. 已知正比例函数的图象经过点M（-1，5）

(1)、求这个函数的表达式；

(2)、若将这个函数的图象向上平移5个单位后，写出图象与 $y$ 轴的交点坐标.

查看试题解析
17. 如图，四边形ABCD中，AB=CD， $∠ A B C = 90 °$ ， $∠ A D C = 90 °$ .求证：AD=BC

查看试题解析
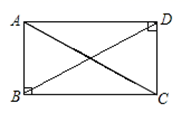18. 如图，方格纸中每个小方格都是长为1个单位的正方形.若学校位置的坐标为A(1，2)，解答以下问题：

(1)、请在图中建立适当的直角坐标系，并写出图书馆B位置的坐标；

(2)、若体育馆位置的坐标为C(－3，3)，请在坐标系中标出体育馆的位置，并顺次连接学校、图书馆、体育馆，得到△ABC，求△ABC的面积.

查看试题解析
19. 如图，在平行四边形ABCD中，E在BC的延长线上，且CE=BC，AE与CD相交于F，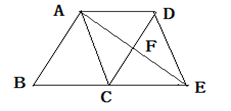

(1)、求证：AC=DE

(2)、若∠BAE=90°，线段AE与CD是什么关系？为什么？

查看试题解析

20. 为了提高学生书写汉字的能力，增强保护汉子的意识，某校举办了首届“汉字听写大赛”，学生经选拔后进入决赛，测试同时听写100个汉字，每正确听写出一个汉字得1分，本次决赛，学生成绩为

（分），且50≤x＜1000，将其按分数段分为五组，绘制出以下不完整表格：

组别	成绩（分）	频数（人数）	频率
一	50≤x＜60	2	0.04
二	60≤x＜70	10	0.2
三	70≤x＜80	14	b
四	80≤x＜90	a	0.32
五	90≤x＜100	8	0.16

请根据表格提供的信息，解答以下问题：

(1)、本次决赛共有名学生参加；

(2)、直接写出表中a= ， b=；

(3)、请补全下面相应的频数分布直方图；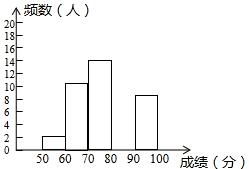

(4)、若决赛成绩不低于80分为优秀，则本次大赛的优秀率为.

查看试题解析

21. 如图，在Rt△ABC中，两锐角的平分线AD，BE相交于O，OF⊥AC于F，OG⊥BC于G.

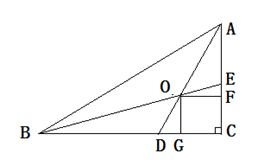(1)、求证：四边形OGCF是正方形.

(2)、若 $∠ B A C = 60 °$ ，AC=4，求正方形OGCF的边长.

查看试题解析
22. 周日，小明一家从家里出发去40公里的郊外野炊，小明和妹妹小红早上8：00骑自行车先走.爸爸和妈妈开车10：00出发，半小时追上小明和小红，随即小明和小红乘坐爸妈的车一起前往目的地.设小明和小红所用的时间为 $x$ （小时），小明和小红所走的路程为 $y_{1}$ （公里），爸妈所走的路程为 $y_{2}$ （公里），图中OCB表示 $y_{1}$ 与 $x$ 之间的函数关系，线段AB表示 $y_{2}$ 与 $x$ 之间的函数关系.

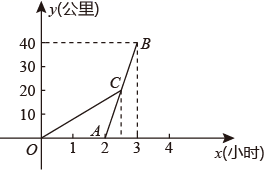(1)、爸妈开车的速度是每小时多少公里？

(2)、求 $y_{1}$ 、 $y_{2}$ 与x的函数表达式.

(3)、如果小明和小红中途不乘坐爸妈的车，继续骑车前往，12：00能到达目的地吗？说明理由.

查看试题解析
23. 如图，直线 $y = \frac{3}{4} x + 6$ 与 $x$ 轴、 $y$ 轴分别交于点A和点B，点C、D分别为线段AB、OB的中点，点P为 $x$ 轴上一动点.

(1)、填空：A点坐标是， B点的坐标是.

(2)、当P是OA的中点时，四边形PCDO是形，其周长是.

(3)、当PC+PD最小时，求P点的坐标.

(4)、是否存在P点，使△PCD是等腰三角形？若存在，请求出P点的坐标.

查看试题解析