湖北省宜昌市伍家岗区2020-2021学年八年级下学期数学期末考试试卷

试卷更新日期：2021-08-10 类型：期末考试

进入 出卷网 下载

一、单选题

  • 1. 下列值中，能满足 a 在实数范围内有意义的是（   ）
    A、a＝﹣2 B、a＝﹣1 C、a＝﹣0.0001 D、a＝2021

    查看试题解析

  • 2. 下列二次根式中，与 3 的积是无理数的是（   ）
    A、13 B、3 C、12 D、6

    查看试题解析

  • 3. 下列计算中，正确的是（   ）
    A、4 ﹣ 3 ＝1 B、3 ＋ 5 ＝ 8 C、2 × 3 ＝ 6 D、8 ÷ 2 ＝4

    查看试题解析

  • 4. 在▱ABCD中，若∠A：∠B＝1：2，则∠A的度数为（   ）
    A、30° B、60° C、120° D、150°

    查看试题解析

  • 5. 如图是一个正方形和直角三角形的组合图形，直角三角形的斜边和一条直角边的长分别为10cm，8cm，则该正方形的面积为（   ）

    A、6cm2 B、36cm2 C、18cm2 D、2cm2

    查看试题解析

  • 6. 如图是一段台阶的截面图，高BC为5米，直角边AC为12米，现打算在台阶上铺上一整张防滑毯，至少需防滑毯的长为（   ）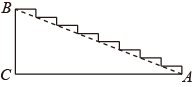

    A、12米 B、13米 C、17米 D、18米

    查看试题解析

  • 7. 如图，E为正方形ABCD的对角线上一点，四边形EFCG为矩形，若正方形ABCD的边长为4，则EG＋GC的长为（   ）

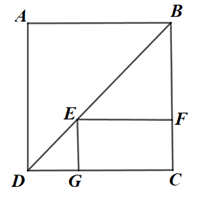    A、4 B、8 C、16 D、32

    查看试题解析

  • 8. 如图，在△ABC中，DE为中位线，连CD，则下列结论不一定成立的是（   ）

    A、BC＝2DE B、∠EDC＝∠BCD C、S△ADC＝S△BDC D、C△ABC＝2C△DEC（代表周长）

    查看试题解析

  • 9. 伍伍同学购买某种粽子每5个花费15元，若花费45元则可购买这种粽子的个数为（   ）
    A、3 B、10 C、15 D、135

    查看试题解析

  • 10. 甲乙两组数据的方差分别为m，n，甲组数据比乙组数据波动小，则n﹣m值为（   ）
    A、正数 B、0 C、负数 D、非负数

    查看试题解析

  • 11. 一次函数y＝kx＋b（k≠0）的图象如图，则不等式kx＋b＞3的解集为（   ）

    A、x＜﹣2.5 B、x＞﹣2.5 C、x＜2 D、x＞2

    查看试题解析

二、填空题

  • 12. 已知x＝ 2 ，y＝﹣ 2 ，则x＋y＝.

    查看试题解析

  • 13. 若改变正方形的边长x，则正方形面积y随之改变.在这个问题中，是自变量.

    查看试题解析

  • 14. 一次函数y＝x＋3与y轴的交点坐标为.

    查看试题解析

  • 15. 从小到大排列的一组数：﹣2，2，2，m，6，7，其中位数为3，则m的值为.

    查看试题解析

三、解答题

  • 16. 计算： 12 ﹣ 9 ÷ 3 .

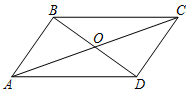
    查看试题解析

  • 17. 判断以12，16，20为边长的三角形的形状.

    查看试题解析

  • 18. 一组数据：0，1，﹣3，6，a，其唯一众数为1，求a的值.

    查看试题解析

  • 19. ▱ABCD的对角线AC，BD交于点O，AB⊥BD，若AB＝4，AC＝10，.求BD的长.

     

    查看试题解析

  • 20. “低碳出行，健康生活”是一种时尚，伍伍同学在晨练中从甲地以速度m匀速步行前往乙地，同时，佳佳同学从乙地沿同一线路以速度n匀速步行前往甲地（m＞n），两人之间的距离y（米）与步行时间x（分钟）之间的函数关系如图所示.

    (1)、说明点B的实际意义；
    (2)、根据图中数据求C的纵坐标.

    查看试题解析

  • 21. Rt△ABC中，∠ACB＝90°，AC＝1，AB＝3，P为斜边AB上一动点，连接CP，E为CP的中点，连接AE并延长至点F，使EF＝AE，连接PF交BC于点G，连接CF.

    (1)、求证：四边形ACFP为平行四边形；
    (2)、连接FB，求点P运动至何处时，CP∥BF？并求此时四边形ABFC的周长.

    查看试题解析

  • 22. 新疆棉花以纤维长、质地柔软、弹性好闻名于世，深受国人青睐.某产销公司现有新疆棉花500吨，全部运往A，B两公司，其中A公司不少于100吨，B公司不少于300吨.已知运往A，B两公司的费用分别为每吨250元和100元.设运往A公司的新疆棉花为x吨.
    (1)、设运往A，B公司的总运费为y元，求y与x之间的函数关系式，并求出自变量x的取值范围；
    (2)、若运往B公司320吨，求总运费；
    (3)、实际运输时，由于前往A地的运输条件（车辆、道路、时间等）大为改善，导致运费每吨减少a元（a＞0），而前往B地的没有变化.若总运费的最小值不小于51000元，求a的取值范围.

    查看试题解析

  • 23. 如图，平行四边形ABCD中，∠A＝30°，AB＝4，∠ABD＝α（0°＜α≤90°），以BD为一边作菱形BDEF，点F在射线BC上，BE与DF交于点O，与CD交于点G，连接GF.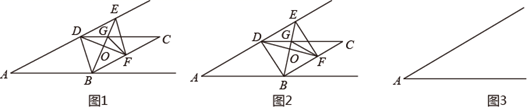

    (1)、如图1，求证：A，D，E三点在一条直线上；
    (2)、如图1，当点F在线段BC上时，求∠DGF的大小（用含α的式子表示）；
    (3)、当△ABD为直角三角形时，求△DFG的面积.

    查看试题解析

  • 24. 在平面直角坐标系中，直线l1：y＝ 43 x＋3m交x轴，y轴于A，E两点，m＞0，过点E的直线l2交x轴正半轴于点B（4m，0），如图1所示.

    (1)、求直线l2的函数解析式；
    (2)、△AEB按角的大小分类为；
    (3)、以点A，B为基础，在x轴上方构建矩形ABCD，点E在边CD上，过原点的直线l3：y＝mx交直线CD于点P交直线AE，BE于点G，H.

    ①若直线l3把矩形ABCD的周长平分，求m的值；

    ②是否存在一个合适的m，使S△BOH＝S△AOG ， 若存在，求m的值；若不存在，则说明理由.

    查看试题解析