湖北省襄阳市枣阳市2020-2021学年八年级下学期数学期末考试试卷
试卷更新日期:2021-08-10 类型:期末考试
一、单选题
-
1. 若代数式 在实数范围内有意义,则x的取值范围是( )A、 B、 C、 D、2. 下列计算正确的是( )A、 B、 C、 D、3. 我市某学校为庆祝中国共产党成立一百周年,开展了“学党史、颂党恩、跟党走”系列主题教育活动.其中,在演讲比赛活动中,参加决赛的所有15位选手的成绩互不相同,在已知自己成绩的情况下,要想知道自己是否能进入前8名,只需要知道这15位选手成绩的( )A、平均数 B、众数 C、中位数 D、方差4. 如图,矩形纸片 ,长 ,宽 ,将其沿 折叠,使点D与点B重合,那么折叠后 的长为( )
 A、 B、 C、 D、5. 如图,是一种古代计时器﹣﹣“漏壶”的示意图,在壶内盛一定量的水,水从壶下的小孔漏出,壶壁内画出刻度,人们根据壶中水面的位置计算时间若用x表示时间,y表示壶底到水面的高度,下面的图象适合表示一小段时间内y与x的函数关系的是( )(不考虑水量变化对压力的影响)
A、 B、 C、 D、5. 如图,是一种古代计时器﹣﹣“漏壶”的示意图,在壶内盛一定量的水,水从壶下的小孔漏出,壶壁内画出刻度,人们根据壶中水面的位置计算时间若用x表示时间,y表示壶底到水面的高度,下面的图象适合表示一小段时间内y与x的函数关系的是( )(不考虑水量变化对压力的影响) A、
A、 B、
B、 C、
C、 D、
D、 6. 2002年国际数学家大会在中国北京举行,这次大会的会徽如图所示,选定的是我国古代数学家赵爽用来证明勾股定理的弦图,可以说是充分肯定了我国数学的成就,也弘扬了我国古代的数学文化.弦图是由四个全等的直角三角形和中间的小正方形拼成的一个大正方形.如果大正方形的面积是18,小正方形的面积是2,直角三角形的较短直角边长为a,较长直角边长为b,那么 的值为( )
6. 2002年国际数学家大会在中国北京举行,这次大会的会徽如图所示,选定的是我国古代数学家赵爽用来证明勾股定理的弦图,可以说是充分肯定了我国数学的成就,也弘扬了我国古代的数学文化.弦图是由四个全等的直角三角形和中间的小正方形拼成的一个大正方形.如果大正方形的面积是18,小正方形的面积是2,直角三角形的较短直角边长为a,较长直角边长为b,那么 的值为( ) A、18 B、30 C、34 D、3647. 一次函数 的图象过点 , ,则( )A、 B、 C、 D、8. 我国宋代数学家秦九韶和古希腊几何学家海伦都曾提出利用三角形的三边求面积的公式,称为海伦﹣秦九韶公式:如果一个三角形的三边长分别是a,b,c,记 ,那么三角形的面积为 .如图,在 中, , , 所对的边分别记为a,b,c,若 , , ,则 的面积为( )
A、18 B、30 C、34 D、3647. 一次函数 的图象过点 , ,则( )A、 B、 C、 D、8. 我国宋代数学家秦九韶和古希腊几何学家海伦都曾提出利用三角形的三边求面积的公式,称为海伦﹣秦九韶公式:如果一个三角形的三边长分别是a,b,c,记 ,那么三角形的面积为 .如图,在 中, , , 所对的边分别记为a,b,c,若 , , ,则 的面积为( )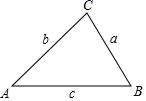 A、 B、 C、24 D、
A、 B、 C、24 D、二、填空题
-
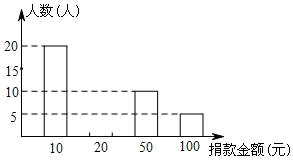
9. 对于任意不相等的两个实数a,b,定义运算※如下: .那么 .10. 每年五月第三个星期日是全国助残日.在今年助残日前夕,某班进行了公益捐款活动,小明对本班同学的捐款情况进行了统计,绘制成如图所示的不完整的统计图,其中捐100元的人数占全班总人数的10%,由统计图可得全班同学平均每人捐款元.
 11. 如图,某港口P位于东西方向的海岸线上,“远航”号、“海天”号轮船同时离开港口,各自沿一固定方向航行,“远航”号每小时航行12nmile,“海天”号每小时航行9nmile,它们离开港口两个小时后分别位于点Q,R处,且相距30nmile.如果知道“远航”号沿北偏东50°方向航行,那么“海天”号沿的方向航行.
11. 如图,某港口P位于东西方向的海岸线上,“远航”号、“海天”号轮船同时离开港口,各自沿一固定方向航行,“远航”号每小时航行12nmile,“海天”号每小时航行9nmile,它们离开港口两个小时后分别位于点Q,R处,且相距30nmile.如果知道“远航”号沿北偏东50°方向航行,那么“海天”号沿的方向航行. 12. 如图,矩形 的对角线 , 相交于点O,且 , ,若 ,则四边形 的周长是.
12. 如图,矩形 的对角线 , 相交于点O,且 , ,若 ,则四边形 的周长是. 13. 一次函数 中,y随x的增大而减小, ,则这个函数的图象不经过第象限.14. 已知一次函数 ( ,m,n为常数),x与y的对应值如下表:
13. 一次函数 中,y随x的增大而减小, ,则这个函数的图象不经过第象限.14. 已知一次函数 ( ,m,n为常数),x与y的对应值如下表:x
-2
-1
0
1
2
3
y
-1
0
1
2
3
4
那么,不等式 的解集是.
15. 如图,在 中,对角线 , 相交于点O,E,F是对角线 上的两点.请补充一个关于点E,F的条件,使四边形 是平行四边形.补充的条件是. 16. 直线 分别与x轴、y轴相交于点B和点D.直线 分别与x轴、y轴相交于点C和点E,直线a与直线b相交于点A,则四边形 的面积为.17. 已知 中, , , 边上的高 ,则边 的长为 .18. 如图,对折矩形纸片 ,使 与 重合得到折痕 ,将纸片展平,再一次折叠,使点A落到 上的点G处,并使折痕经过点B,交 于点H,交 于点M.已知 ,则线段 的长度为.
16. 直线 分别与x轴、y轴相交于点B和点D.直线 分别与x轴、y轴相交于点C和点E,直线a与直线b相交于点A,则四边形 的面积为.17. 已知 中, , , 边上的高 ,则边 的长为 .18. 如图,对折矩形纸片 ,使 与 重合得到折痕 ,将纸片展平,再一次折叠,使点A落到 上的点G处,并使折痕经过点B,交 于点H,交 于点M.已知 ,则线段 的长度为.
三、解答题
-
19. 计算:(1)、(2)、20. 如图,在正方形 中,E是 边的中点,F是 上一点且 ,连接 , ,
求证: .
 21. 已知 , ,求下列各式的值:(1)、 ;(2)、 .22. 我市在推进城乡生活垃圾分类的行动中,某社区为了了解居民掌握垃圾分类知识的情况进行调查.其中A,B两小区分别有300名居民参加了测试,社区从中各随机抽取50名居民成绩进行整理得到部分信息:
21. 已知 , ,求下列各式的值:(1)、 ;(2)、 .22. 我市在推进城乡生活垃圾分类的行动中,某社区为了了解居民掌握垃圾分类知识的情况进行调查.其中A,B两小区分别有300名居民参加了测试,社区从中各随机抽取50名居民成绩进行整理得到部分信息:(信息一)A小区50名居民成绩的频数直方图如图(每一组含前一个边界值,不含后一个边界值):

(信息二)上图中,从左往右第四组的成绩如下:
75
75
79
79
79
79
80
80
81
82
82
83
83
84
84
84
(信息三)A、B两小区各50名居民成绩的平均数、中位数、众数、优秀率(80分及以上为优秀)、方差等数据如下(部分空缺):
小区
平均数
中位数
众数
优秀率
方差
A
75.1
x
79
40%
277
B
75.1
77
76
45%
211
根据以上信息,回答下列问题:
(1)、填空: ;(2)、请估计A小区300名居民成绩能超过平均数的人数.(3)、请从两个角度,选择合适的统计量分析A,B两小区参加测试的居民掌握垃圾分类知识的情况.23. 如图,在 中, ,点E是斜边 的中点. (1)、过点C作 于点D(尺规作图,保留痕迹,不写作法);(2)、若 ,求 的度数.24. 在“看图说故事”活动中,某学习小组结合图象设计了一个问题情境.已知小亮所在学校的宿舍、食堂、图书馆依次在同一条直线上,食堂离宿舍 ,图书馆离宿舍 .周末,小亮从宿舍出发,匀速走了 到食堂;在食堂停留 吃早餐后,匀速走了 到图书馆;在图书馆停留 借书后,匀速走了 返回宿舍.给出的图象反映了这个过程中小亮离宿舍的距离 与离开宿舍的时间 之间的对应关系.
(1)、过点C作 于点D(尺规作图,保留痕迹,不写作法);(2)、若 ,求 的度数.24. 在“看图说故事”活动中,某学习小组结合图象设计了一个问题情境.已知小亮所在学校的宿舍、食堂、图书馆依次在同一条直线上,食堂离宿舍 ,图书馆离宿舍 .周末,小亮从宿舍出发,匀速走了 到食堂;在食堂停留 吃早餐后,匀速走了 到图书馆;在图书馆停留 借书后,匀速走了 返回宿舍.给出的图象反映了这个过程中小亮离宿舍的距离 与离开宿舍的时间 之间的对应关系.
请根据相关信息,解答下列问题:
(1)、填表:离开宿舍的时间/min
2
5
20
23
30
离宿舍的距离/km
0.2
a
0.7
0.7
b
(2)、填空:①食堂到图书馆的距离为km;
②小亮从图书馆返回宿舍的速度为km/min;
③当小亮离宿舍的距离为0.6km时,他离开宿舍的时间为min.
(3)、当 和 时,请分别直接写出y关于x的函数解析式.25. 如图,点A,F,C,D在同一条直线上,点B,E分别在直线 两侧,且 , , . (1)、求证:四边形 是平行四边形;(2)、若 , , ,当 为何值时,四边形 是菱形.26. 为提高学生的身体素质,我市某学校积极开展“阳光体育运动”.引导学生走向操场、走进大自然、走到阳光下,积极参加体育锻炼.为满足学生需求,保障“阳光体育运动”的开展,让更多的学生以更大的兴趣、更多的时间积极投入到运动之中.学校现计划从某体育用品专卖店购进足球和篮球共100个,足球的售价为每个80元.购买篮球所需费用y(元)与购买数量x(个)之间存在如图所示的函数关系.
(1)、求证:四边形 是平行四边形;(2)、若 , , ,当 为何值时,四边形 是菱形.26. 为提高学生的身体素质,我市某学校积极开展“阳光体育运动”.引导学生走向操场、走进大自然、走到阳光下,积极参加体育锻炼.为满足学生需求,保障“阳光体育运动”的开展,让更多的学生以更大的兴趣、更多的时间积极投入到运动之中.学校现计划从某体育用品专卖店购进足球和篮球共100个,足球的售价为每个80元.购买篮球所需费用y(元)与购买数量x(个)之间存在如图所示的函数关系. (1)、直接写出当 和 时,y与x之间的函数关系式;(2)、若在购买计划中,篮球的数量不超过60个,但不少于35个.学校如何分配篮球和足球的购买数量,可使得购买总费用最低,并求出最低费用.27. 在正方形 中,点E为射线 上一点,连接 ,过点E作 交射线 于点F,以 , 为邻边作矩形 ,连接 .
(1)、直接写出当 和 时,y与x之间的函数关系式;(2)、若在购买计划中,篮球的数量不超过60个,但不少于35个.学校如何分配篮球和足球的购买数量,可使得购买总费用最低,并求出最低费用.27. 在正方形 中,点E为射线 上一点,连接 ,过点E作 交射线 于点F,以 , 为邻边作矩形 ,连接 .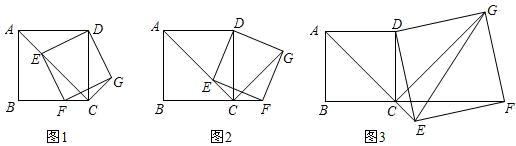 (1)、发现问题:如图1,当点E在线段 上时.
(1)、发现问题:如图1,当点E在线段 上时.①求证四边形 是正方形;
②猜想 与 之间的数量关系,并说明理由.
(2)、类比探究:当点E运动到如图2所示的位置时,求 的度数.(3)、拓展运用:如图3,当点E在线段 的延长线上时,若正方形 的边长为4, ,求 的长.