12.1 全等三角形 同步练习----初中数学人教版八年级上册
试卷更新日期:2021-08-10 类型:同步测试
一、单选题
-
1. 下列各选项中的两个图形属于全等形的是( )A、

B、
B、
C、
C、
D、
D、
2. 已知图中的两个三角形全等,则∠α的度数是( )
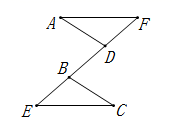
2. 已知图中的两个三角形全等,则∠α的度数是( ) A、80° B、60° C、90° D、50°3. 如图,点B,E,C,F在一条直线上, ,则下列结论正确的是( )
A、80° B、60° C、90° D、50°3. 如图,点B,E,C,F在一条直线上, ,则下列结论正确的是( )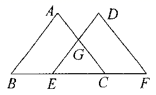 A、 B、 C、 D、4. 如图,已知△ABC≌△DEF,若AC=22,CF=4,则CD的长是( )
A、 B、 C、 D、4. 如图,已知△ABC≌△DEF,若AC=22,CF=4,则CD的长是( ) A、22 B、18 C、16 D、45. 如图, , , , ,垂足分别为A、B.点P从点A出发,以每秒2个单位的速度沿 向点B运动;点Q从点B出发,以每秒a个单位的速度沿射线 方向运动.点P、点Q同时出发,当以P、B、Q为顶点的三角形与 全等时,a的值为( )
A、22 B、18 C、16 D、45. 如图, , , , ,垂足分别为A、B.点P从点A出发,以每秒2个单位的速度沿 向点B运动;点Q从点B出发,以每秒a个单位的速度沿射线 方向运动.点P、点Q同时出发,当以P、B、Q为顶点的三角形与 全等时,a的值为( )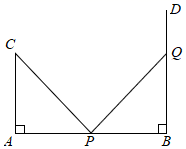 A、2 B、3 C、2或3 D、2或6. 下列说法中正确的是( )A、两个面积相等的图形,一定是全等图形 B、两个等边三角形是全等图形 C、两个全等图形的面积一定相等 D、若两个图形周长相等,则它们一定是全等图形7. 如图是由四个全等的直角三角形与一个小正方形拼成的大正方形.若小正方形边长为 ,大正方形边长为 ,则一个直角三角形的面积等于( )
A、2 B、3 C、2或3 D、2或6. 下列说法中正确的是( )A、两个面积相等的图形,一定是全等图形 B、两个等边三角形是全等图形 C、两个全等图形的面积一定相等 D、若两个图形周长相等,则它们一定是全等图形7. 如图是由四个全等的直角三角形与一个小正方形拼成的大正方形.若小正方形边长为 ,大正方形边长为 ,则一个直角三角形的面积等于( ) A、 B、 C、 D、8.
A、 B、 C、 D、8.如图:Rt△ABC≌Rt△DEF,则∠D的度数为( )
 A、30° B、45° C、60° D、90°9. 如图,AD=BC,∠C=∠D=90°,下列结论中不成立的是( )
A、30° B、45° C、60° D、90°9. 如图,AD=BC,∠C=∠D=90°,下列结论中不成立的是( ) A、∠DAE=∠CBE B、CE=DE C、△DAE与△CBE不一定全等 D、∠1=∠210. 如图,锐角△ABC 中,D 、E 分别是 AB 、AC 边上的点,△ADC≌△ADC',△AEB≌△AEB' , 且C'D∥EB'∥BC , BE 、CD 交于点 F ,若∠BAC = α, ∠BFC = β,则( )
A、∠DAE=∠CBE B、CE=DE C、△DAE与△CBE不一定全等 D、∠1=∠210. 如图,锐角△ABC 中,D 、E 分别是 AB 、AC 边上的点,△ADC≌△ADC',△AEB≌△AEB' , 且C'D∥EB'∥BC , BE 、CD 交于点 F ,若∠BAC = α, ∠BFC = β,则( ) A、2α+β= 180° B、2β-α= 145° C、α+β= 135° D、β-α= 60°
A、2α+β= 180° B、2β-α= 145° C、α+β= 135° D、β-α= 60°二、填空题
-
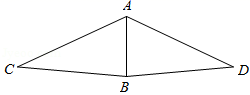
11. 一个三角形的三条边长分别为 , ,x,另一个三角形的三条边长分别为y, , ,若这两个三角形全等,则 .12. 如图, , , ,则 的度数为.
 13. 如图,△ABC≌△DEF,请根据图中提供的信息,写出x= , ∠E=.
13. 如图,△ABC≌△DEF,请根据图中提供的信息,写出x= , ∠E=. 14. 如图,△ABC≌△BAE,∠ABE=60°,∠E=80°,则∠ABC=°.
14. 如图,△ABC≌△BAE,∠ABE=60°,∠E=80°,则∠ABC=°. 15. 如图所示,ΔBKC≌ΔBKE≌ΔDKC, BE与KD交于点G, KE与CD交于点P, BE与CD交于点A,∠BKC=134°,∠E= 22° ,则∠KPD=.
15. 如图所示,ΔBKC≌ΔBKE≌ΔDKC, BE与KD交于点G, KE与CD交于点P, BE与CD交于点A,∠BKC=134°,∠E= 22° ,则∠KPD=.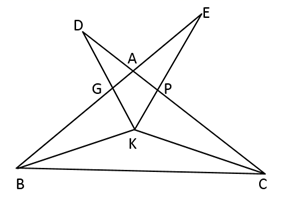 16. 如图,在△ABC中,AB=AC=24厘米,∠B=∠C ,BC=16厘米,点D为AB的中点,点P在线段BC上以4厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.当点Q的运动速度为厘米/秒时,能够在某一时刻使△BPD与△CQP全等.
16. 如图,在△ABC中,AB=AC=24厘米,∠B=∠C ,BC=16厘米,点D为AB的中点,点P在线段BC上以4厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.当点Q的运动速度为厘米/秒时,能够在某一时刻使△BPD与△CQP全等.
三、解答题
-
17. 已知:如图,点D在△ABC的BC边上,AC∥BE,BC=BE,∠ABC=∠E,求证:AB=DE.
 18. 如图所示,已知△ABD≌△ACD,且B,D,C在同一条直线上,那么AD与BC是怎样的位置关系?为什么?
18. 如图所示,已知△ABD≌△ACD,且B,D,C在同一条直线上,那么AD与BC是怎样的位置关系?为什么? 19. 如图,△ABO≌△CDO,点B在CD上,AO∥CD,∠BOD=30°,求∠A的度数.
19. 如图,△ABO≌△CDO,点B在CD上,AO∥CD,∠BOD=30°,求∠A的度数.
四、作图题