湖北省襄阳市樊城区2020-2021学年八年级下学期数学期末考试试卷

试卷更新日期：2021-08-10 类型：期末考试

进入出卷网下载

一、单选题

1. 如图，数轴上的A、B、C、D四点中，与数﹣ $\sqrt{3}$ 表示的点最接近的是（）

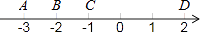A、点A B、点B C、点C D、点D

查看试题解析
2. 下列二次根式中，与 $\sqrt{3}$ 是同类二次根式的是（　　）

A、 $\sqrt{18}$ B、 $\sqrt{\frac{1}{3}}$ C、 $\sqrt{24}$ D、 $\sqrt{0.3}$

查看试题解析
3. 下列长度的三条线段能组成直角三角形的是（）

A、3，4，5 B、10，15，20 C、1， $\sqrt{2}$ ，3 D、2，3，4

查看试题解析
4. 如图，点E在正方形ABCD的边AB上，若EB＝1，EC＝2，那么正方形ABCD的面积为（）

A、 $\sqrt{3}$ B、3 C、 $\sqrt{5}$ D、5

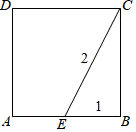查看试题解析
5. 如图，在△ABC中，D，E分别是AB，BC的中点，点F在DE延长线上，添加一个条件使四边形ADFC为平行四边形，则这个条件是（）

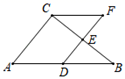A、∠B＝∠F B、∠B＝∠BCF C、AC＝CF D、AD＝CF

查看试题解析
6. 某校男子篮球队10名队员进行定点投篮练习，每人投篮10次，他们投中的次数统计如表：

投中次数

3

5

6

7

8

人数

1

3

2

2

2

则这些队员投中次数的众数、中位数分别为（）

A、5，6 B、2，6 C、5，5 D、5，5.5

查看试题解析
7. 若直线y＝kx＋b不经过第一象限，则（）

A、k＞0，b＜0 B、k＜0，b≤0 C、k＜0，b≥0 D、k＜0，b＞0

查看试题解析
8. 如果一个四边形的对角线相等，顺次连接该四边形四条边的中点，可以得到（）

A、平行四边形 B、矩形 C、菱形 D、正方形

查看试题解析
9. 我国古代数学家刘徽将勾股形（古人称直角三角形为勾股形）分割成一个正方形和两对全等的三角形，如图所示，已知 $∠ A = 90^{°}$ ， $B D = 4$ ， $C F = 6$ ，则正方形ADOF的边长是（）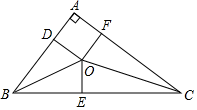

A、 $\sqrt{2}$ B、2 C、 $\sqrt{3}$ D、4

查看试题解析
10. 某快递公司每天上午9：00～10：00为集中揽件和派件时段，甲仓库用来揽收快件，乙仓库用来派发快件，该时段内甲，乙两仓库的快件数量 $y$ （件）与时间 $x$ （分）之间的函数图象如图所示，那么当两仓库快递件数相同时，此刻的时间为（）

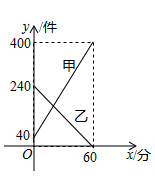A、9：15 B、9：20 C、9：25 D、9：30

查看试题解析

二、填空题

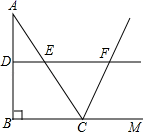
11. 若式子 $\frac{\sqrt{x - 2}}{x - 3}$ 有意义，则x的取值范围为.

查看试题解析
12. $\sqrt{2}$ ＋ $\sqrt{8}$ － $\sqrt{32}$ ＝.

查看试题解析
13. 若一次函数 $y = x^{k^{2} - 3} - k$ 不经过第四象限，则k的值为.

查看试题解析
14. 若三点（1，4），（2，7），（a，10）在同一直线上，则a的值等于．

查看试题解析
15. 如图，在△ABC中，∠ABC＝90°，AB＝4，BC＝3.若DE是△ABC的中位线，延长DE交△ABC的外角平分线于点F，则线段DF的长为.

查看试题解析
16. 在一张直角三角形纸片中，分别沿两直角边上一点与斜边中点的连线剪去两个三角形，得到如图所示的四边形，则原直角三角形纸片的斜边长是.

查看试题解析

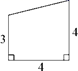
三、解答题

17. 计算： ${(\sqrt{3} - 2)}^{2} + \sqrt{12} + 6 \sqrt{\frac{1}{3}}$

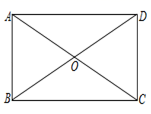
查看试题解析
18. 先化简，再求值： ${(\frac{a + b}{a - b})}^{2} • \frac{2 a - 2 b}{3 a + 3 b} - \frac{4 a^{2}}{a^{2} - b^{2}} \div \frac{3 a}{b}$ ，其中 $a = \sqrt{3} ， b = \sqrt{2}$ .

查看试题解析
19. 如图，已知 $▱$ ABCD的对角线AC、BD相交于点O，∠OBC＝∠OCB.

(1)、求证： $▱$ ABCD是矩形；

(2)、若AB＝6，BO＝5，求该矩形的面积.

查看试题解析
20. 在△ABC中，AB，BC，AC三边的长分别为 $\sqrt{5} ， \sqrt{10} ， \sqrt{13}$ ，求这个三角形的面积，小辉同学在解答这道题时，先建立一个正方形网格（每个小正方形的边长为1），再在网格中画出格点△ABC（即三个顶点都在小正方形的顶点处，如图1所示，这样不需要求△ABC的高，而借用网格就能计算出它的面积.）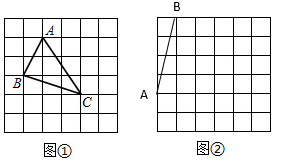

(1)、请将△ABC的面积直接填写在横线上.

(2)、我们把上述求△ABC面积的方法叫做构图法，若△ABC三边的长分别为 $\sqrt{5} a$ ，2 $\sqrt{2} a ， \sqrt{17} a$ （a＞0），请在图②中给出的正方形网格内（每个小正方形的边长为a）画出相应的△ABC（其中一条边已经画好），并求出它的面积.

查看试题解析
21. 高尔基说：“书，是人类进步的阶梯.”阅读可以丰富知识、拓展视野、充实生活等诸多益处.为了解学生的课外阅读情况，某校随机抽查了部分学生阅读课外书册数的情况，并绘制出如下统计图.其中条形统计图因为破损丢失了阅读5册书数的数据.

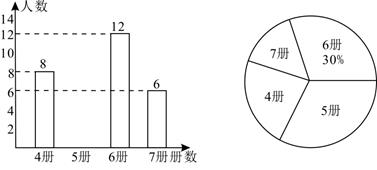(1)、求条形图中丢失的数据，并写出阅读书册数的众数和中位数；

(2)、根据随机抽查的这个结果，请估计该校1200名学生中课外阅读5册书的学生人数；

(3)、若学校又补查了部分同学的课外阅读情况，得知这部分同学中课外阅读最少的是6册，将补查的情况与之前的数据合并后发现中位数并没有改变，试求最多补查了多少人？

查看试题解析
22. 如图：已知直线y₁＝kx＋b经过点A（5，0），B（1，4），与直线y₂＝2x﹣4交于C点.

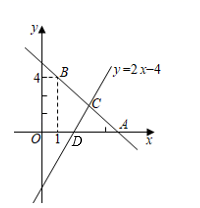(1)、求直线y₁的解析式以及y₂与x轴的交点D的坐标；

(2)、求C点的坐标；

(3)、根据图象，直接写出关于x的不等式y₁＞y₂＞0时x的取值范围.

查看试题解析
23. 如图，矩形ABCD中，AB＝8，BC＝6，P点从D点出发向C点运动，Q点从B点同时出发向A点运动，P、Q的运动速度相等，均为每秒1个单位，当任意一点到达终点时，另一点也停止运动.

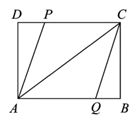(1)、没到达终点前，求证：以点A、Q、C、P为顶点的四边形为平行四边形；

(2)、点A、Q、C、P组成的四边形为菱形时，运动时间t＝；

(3)、当△ADP为等腰三角形时，由点A、Q、C、P组成的四边形面积为.

查看试题解析
24. 在菱形 ABCD 中， ∠ABC=60°，点 P 是射线 BD 上一动点，以 AP 为边向右侧作等边 △APE ，点 E 的位置随点 P 的位置变化而变化.

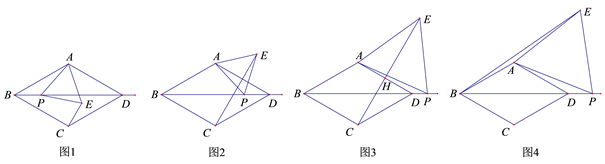(1)、如图1，当点 E 在菱形ABCD内部或边上时，连接CE ， BP 与 CE 的数量关系是， CE 与 AD 的位置关系是；

(2)、当点 E 在菱形ABCD外部时，(1)中的结论是否还成立？若成立，请予以证明；若不成立，请说明理由(选择图2，图3中的一种情况予以证明或说理).

(3)、如图4，当点 P 在线段 BD 的延长线上时，连接 BE ，若 $A B = 2 \sqrt{3}$ ， $B E = 2 \sqrt{19}$ ，求四边形 ADPE 的面积.

查看试题解析
25. 某超市准备购进A、B两种商品，进3件A，4件B需要270元；进5件A，2件B需要310元；该超市将A种商品每件的售价定为80元，B种商品每件的售价定为45元.

(1)、A种商品每件的进价和B种商品每件的进价各是多少元？

(2)、商店计划用不超过1560元的资金购进A、B两种商品共40件，其中A种商品的数量不低于B种商品数量的一半，该商店有几种进货方案？

(3)、端午节期间，商店开展优惠促销活动，决定对每件A种商品售价优惠m（10＜m＜20）元，B种商品售价不变，在（2）的条件下，请设计出m的不同取值范围内，销售这40件商品获得总利润最大的进货方案.

查看试题解析

投中次数	3	5	6	7	8
人数	1	3	2	2	2