湖北省武汉市武昌区2020-2021学年八年级下学期期末数学试卷
试卷更新日期:2021-08-10 类型:期末考试
一、单选题
-
1. 二次根式 在实数范围内有意义,则 满足的条件是( )A、 B、 C、 D、2. 下列二次根式中,与 是同类二次根式的是( )A、 B、 C、 D、3. 若一次函数 的图象与 轴交于点 ,则点 的坐标为( )A、 B、 C、 D、4. 某校对九年级6个班学生平均一周的课外阅读时间进行了统计,分别为(单位:h):3.5,4,3.5,5,5,3.5.这组数据的众数是( )A、3 B、3.5 C、4 D、55. 下列计算正确的是( )A、 B、 C、 D、6. 在 中, , ,若 ,则 的长为( )A、 B、 C、 D、7. 在课外活动中,有10名同学进行了投篮比赛,限每人投10次,投中次数与人数如下表:
投中次数
5
7
8
9
10
人数
2
3
3
1
1
则这10人投中次数的平均数是( )
A、7 B、7.2 C、7.4 D、7.58. 如图, ABCD中,对角线AC和BD交于点O,若AC=8,BD=6,则边AB长的取值范围是( ) A、1<AB<7 B、2<AB<14 C、6<AB<8 D、3<AB<49. 在平面直角坐标系中,过点(-2,3)的直线l经过一、二、三象限,若点(0,a)、(-1,b)、(C,-1)都在直线l 上,则下列判断正确的是( )A、a< b B、a< 3 C、b< 3 D、c< -210. 在 中,点 在 上, , ,则 的长是( )
A、1<AB<7 B、2<AB<14 C、6<AB<8 D、3<AB<49. 在平面直角坐标系中,过点(-2,3)的直线l经过一、二、三象限,若点(0,a)、(-1,b)、(C,-1)都在直线l 上,则下列判断正确的是( )A、a< b B、a< 3 C、b< 3 D、c< -210. 在 中,点 在 上, , ,则 的长是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
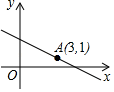
11. 化简: .12. 将直线 向上平移 个单位长度,所得的直线解析式为.13. 如图,直线 经过点 ,当 时, 的取值范围为 .
 14. 某校抽样调查了七年级学生每天体育锻炼时间,整理数据后制成了如下所示的频数分布表,这个样本的中位数在第 组.
14. 某校抽样调查了七年级学生每天体育锻炼时间,整理数据后制成了如下所示的频数分布表,这个样本的中位数在第 组.组别
时间(小时)
频数(人)
第1组
0≤t<0.5
12
第2组
0.5≤t<1
24
第3组
1≤t<1.5
18
第4组
1.5≤t<2
10
第5组
2≤t<2.5
6
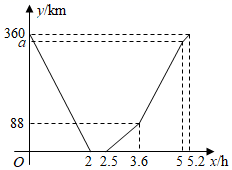
15. 快车从甲地驶往乙地,慢车从乙地驶往甲地,两车同时出发并且在同一条公路上匀速行驶.图中折线表示快、慢两车之间的路程 与它们的行驶时间 之间的函数关系.杜伟同学结合图象得出如下结论:①快车途中停留了 ;
②快车速度比慢车速度多 ;
③图中 ;
④快车先到达目的地.
其中正确的是.(填序号)
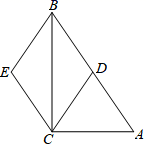
 16. 如图是一张面积为 的 纸片,其中 , , 是三角形的中位线, , 分别是线段 , 上的动点.沿着虚线将纸片裁开,并将 两侧的纸片按箭头所示的方向分别绕点 , 旋转 在同一平面内拼图,使得 与 重合, 与 重合.则拼成的四边形纸片周长的最大值与最小值之差为.
16. 如图是一张面积为 的 纸片,其中 , , 是三角形的中位线, , 分别是线段 , 上的动点.沿着虚线将纸片裁开,并将 两侧的纸片按箭头所示的方向分别绕点 , 旋转 在同一平面内拼图,使得 与 重合, 与 重合.则拼成的四边形纸片周长的最大值与最小值之差为.
三、解答题
-
17. 计算:(1)、 ;(2)、 .18. 如图,在 中, , 为 边上的中线,过点 作 ,过点 作 , 与 相交于点 .求证:四边形 为菱形.
 19. 某校九年级两个班,各选派10名学生参加学校举行的“汉字听写”大赛预赛.各参赛选手的成绩如下:
19. 某校九年级两个班,各选派10名学生参加学校举行的“汉字听写”大赛预赛.各参赛选手的成绩如下:九(1)班:88,91,92,93,93,93,94,98,98,100.
九(2)班:89,93,93,93,95,96,96,98,98,99 ,
通过整理,得到数据分析表如下:
班级
最高分
平均分
中位数
众数
方差
九(1)班
100
93
93
12
九(2)班
99
95
93
8.4
(1)、求表中 , 的值;(2)、依据数据分析表,说明是(1)班的成绩好还是(2)班的成绩好?请给出两条理由.20. 如图,在正方形 纸片上有一点 , , , .现将 剪下,并将在拼到如图所示 位置( 与 重合, 与 重合, 与 重合). (1)、求线段 的长;(2)、求 的度数21. 如图,在 的方格纸中, 的顶点均在格点上,仅用无刻度的直尺按要求画图.
(1)、求线段 的长;(2)、求 的度数21. 如图,在 的方格纸中, 的顶点均在格点上,仅用无刻度的直尺按要求画图. (1)、在图 中画一个以 , , , 为顶点的平行四边形,且 为格点;(2)、在图 中作直线 ( 为格点);(3)、在图 中作 ( 为格点,且不在直线 上).22. 武汉的夏季到了,某服装店同时购进 , 两款夏装共 套,进价和售价如下表所示,设购进 款夏装 套( 为正整数),该服装店售完全部 , 两款夏装获得的总利润为 元.
(1)、在图 中画一个以 , , , 为顶点的平行四边形,且 为格点;(2)、在图 中作直线 ( 为格点);(3)、在图 中作 ( 为格点,且不在直线 上).22. 武汉的夏季到了,某服装店同时购进 , 两款夏装共 套,进价和售价如下表所示,设购进 款夏装 套( 为正整数),该服装店售完全部 , 两款夏装获得的总利润为 元.夏装款式
款
款
每套进价(单位:元)
60
80
每套售价(单位:元)
100
150
(1)、求 与 的函数关系式;(2)、该服装店计划投入不多于2万元购进这两款夏装,则至少购进多少套 款夏装?若 , 两款夏装全部售完,则服装店可获得的最大利润是多少元?(3)、在(2)的条件下,服装店购进 款夏装的进价降低 元(其中 ),购进 款夏装的进价不变,且最多购进 套 款夏装.若保持这两款夏装的售价不变,该服装店如何进货使得全部售完 , 两款夏装获得的利润最大?23. 如图,四边形 是边长为 的正方形, 为线段 上一动点, ,垂足为 . (1)、如图1,连接 交 于点 ,若 ,求 的长;(2)、如图2,点 在 的延长线上,点 在 上运动时,满足 ,
(1)、如图1,连接 交 于点 ,若 ,求 的长;(2)、如图2,点 在 的延长线上,点 在 上运动时,满足 ,①连接 , ,判断 , 的数量关系并说明理由;
②如图 ,若 为 的中点,直接写出 的最小值为 ▲ .
24. 如图,在平面直角坐标系 中,直线 : 与直线 : 相交于点 ,分别交坐标轴于点 , , , . (1)、求 和 的值;(2)、如图,点 是直线 上的一个动点,当 的面积为 时,求点 的坐标;(3)、直线 上有一点 ,在平面直角坐标系内找一点 ,使得以 为一边,以点 , , , 为顶点的四边形是菱形,请直接写出符合条件的点 的坐标.
(1)、求 和 的值;(2)、如图,点 是直线 上的一个动点,当 的面积为 时,求点 的坐标;(3)、直线 上有一点 ,在平面直角坐标系内找一点 ,使得以 为一边,以点 , , , 为顶点的四边形是菱形,请直接写出符合条件的点 的坐标.