湖北省武汉市硚口区2020-2021学年八年级下学期期末数学试卷
试卷更新日期:2021-08-10 类型:期末考试
一、单选题
-
1. 函数 的自变量x的取值范围是( )A、 B、 C、 D、2. 下列计算正确的是( )A、 B、 C、 D、3. 下列各曲线中表示y是x的函数的是( )A、
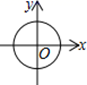 B、
B、 C、
C、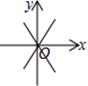 D、
D、 4. 由下列条件不能判定为直角三角形的是( )A、 B、 C、 D、5. 一次函数 的图象经过( )A、第一、三、四象限 B、第一、二、三象限 C、第一、二、四象限 D、第二、三、四象限6. 调查某班10名学生一周居家劳动的时间(单位:h),统计结果如下表:
4. 由下列条件不能判定为直角三角形的是( )A、 B、 C、 D、5. 一次函数 的图象经过( )A、第一、三、四象限 B、第一、二、三象限 C、第一、二、四象限 D、第二、三、四象限6. 调查某班10名学生一周居家劳动的时间(单位:h),统计结果如下表:一周劳动时间
4
5
6
7
人数
2
3
4
1
这么这10名学生一周内的平均劳动时间为( )
A、 B、 C、 D、7. 某种瓜苗早期在农科所温室中生长,长到 时,移至村庄的大棚内沿插杆继续向上生长.研究表明,60天内,这种瓜苗的平均高度 与生长时间x(天)的函数关系的图象如图所示.当这种瓜苗长到大约 时,开始开花,则这种瓜苗移至大棚后,继续生长至开始开花所用的时间是( ) A、33天 B、18天 C、35天 D、20天8. 如图,点O为矩形ABCD的对称中心,点E从点A出发沿AB向点B运动,移动到点B停止,延长EO交CD于点F,则四边形AECF形状的变化依次为( )
A、33天 B、18天 C、35天 D、20天8. 如图,点O为矩形ABCD的对称中心,点E从点A出发沿AB向点B运动,移动到点B停止,延长EO交CD于点F,则四边形AECF形状的变化依次为( ) A、平行四边形→正方形→平行四边形→矩形 B、平行四边形→菱形→平行四边形→矩形 C、平行四边形→正方形→菱形→矩形 D、平行四边形→菱形→正方形→矩形9. 如图,在菱形 中,M、N分别是 和 的中点, 于点P,连接 ,若 ,则 ( )
A、平行四边形→正方形→平行四边形→矩形 B、平行四边形→菱形→平行四边形→矩形 C、平行四边形→正方形→菱形→矩形 D、平行四边形→菱形→正方形→矩形9. 如图,在菱形 中,M、N分别是 和 的中点, 于点P,连接 ,若 ,则 ( )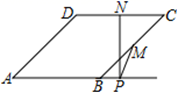 A、 B、 C、 D、10. 已知 ,则 的值是( )A、 B、 C、 D、
A、 B、 C、 D、10. 已知 ,则 的值是( )A、 B、 C、 D、二、填空题
-
11. 求值: .12. 测量7名学生的体温(单位:℃)如下:36.5、36.3、36.8、36.3、36.5、36.7、36.5,这组数据的众数和中位数分别是℃、℃.13. 方程 的解是 .14. 如图,点A、B、C在水平地面的同一条直线上,发射塔 于点C,测得 则 m.( 取1.732,按四舍五入法把结果精确0.1)
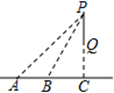 15. 直线l: (k、b是常数, )经过 、 两点,其中 ,下列四个结论:①方程 的解在 和0之间;②若点 、 在直线l上,则 ;③ ;④不等式 的解集为 时, ,其中正确的结论有.(只需填写序号)16. 如图,点E、G分别是正方形 的 、 边的中点,点F、H在对角线 上.若四边形 是矩形,则 .
15. 直线l: (k、b是常数, )经过 、 两点,其中 ,下列四个结论:①方程 的解在 和0之间;②若点 、 在直线l上,则 ;③ ;④不等式 的解集为 时, ,其中正确的结论有.(只需填写序号)16. 如图,点E、G分别是正方形 的 、 边的中点,点F、H在对角线 上.若四边形 是矩形,则 .
三、解答题
-
17. 一次函数的图象经过 、 两点,求这个一次函数的解析式.18. 如图,在 中, 于E,点F在边 上, ,求证:四边形 是矩形.
 19. 新学期,某校开设了“防疫宣传”“心理疏导”等课程,童威为了解学生对新开设课程的掌握情况,从八年级学生中随机抽取了部分学生进行了一次综合测试.测试结果分为四个等级:A级为优秀,B级为良好,C级为及格,D级为不及格.将测试结果绘制了两幅不完整的统计图.根据统计图中的信息解答下列问题:
19. 新学期,某校开设了“防疫宣传”“心理疏导”等课程,童威为了解学生对新开设课程的掌握情况,从八年级学生中随机抽取了部分学生进行了一次综合测试.测试结果分为四个等级:A级为优秀,B级为良好,C级为及格,D级为不及格.将测试结果绘制了两幅不完整的统计图.根据统计图中的信息解答下列问题: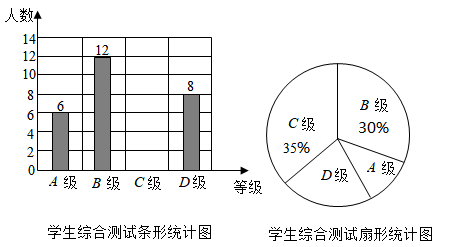 (1)、本次抽样测试的学生人数是名;(2)、扇形统计图中表示A级的扇形圆心角的大小是 ▲ ,并把条形统计图补充完整;(3)、该校八年级共有学生800名学生参加这次测试,估计测试结果是A级的学生人数.20. 由边长为1的正方形构成网格,每个小正方形的顶点叫做格点.仅用无刻度的直尺在给定网格中完成画图,画图过程用虚线表示,画图结果用实线表示.
(1)、本次抽样测试的学生人数是名;(2)、扇形统计图中表示A级的扇形圆心角的大小是 ▲ ,并把条形统计图补充完整;(3)、该校八年级共有学生800名学生参加这次测试,估计测试结果是A级的学生人数.20. 由边长为1的正方形构成网格,每个小正方形的顶点叫做格点.仅用无刻度的直尺在给定网格中完成画图,画图过程用虚线表示,画图结果用实线表示.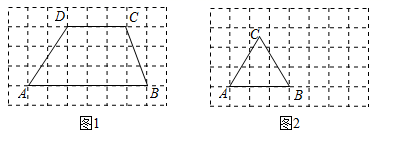 (1)、如图1,四边形 的顶点都是格点画 ,在 上画点F,使 平分 的面积.(2)、如图2,等边 的顶点A、B都是格点
(1)、如图1,四边形 的顶点都是格点画 ,在 上画点F,使 平分 的面积.(2)、如图2,等边 的顶点A、B都是格点①画 的高 ;
②画 的高 .
21. 如图,直线 与直线 交于点C,它们与y轴分别交于A、B两点.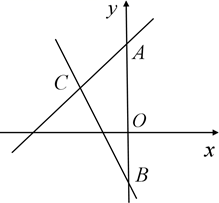 (1)、求A、B、C三点的坐标(2)、点F在x轴正半轴上,使 ,求点F的坐标;(3)、点P在x轴上,使 ,直接写出点P的坐标;22. 某校计划购买A、B两种防疫物资共200套,要求A种物资数量不低于B种物资数量的 ,且不高于B种物资数量的 ,A、B两种物资的单价分别是150元/套、100元/套.设购买A种物资x套,购买这两种物资所需的总费用为y元.(1)、直接写出y关于x的函数关系式;(2)、求总费用y的最小值;(3)、若实际购买时,A种物资单价下调 元/套,B种物资单价上调了m元/套,此时购买这两种物资所需最少费用为23500元,直接写出m的值.23. 已知正方形 的对角线 、 交于O,M是 上一点.
(1)、求A、B、C三点的坐标(2)、点F在x轴正半轴上,使 ,求点F的坐标;(3)、点P在x轴上,使 ,直接写出点P的坐标;22. 某校计划购买A、B两种防疫物资共200套,要求A种物资数量不低于B种物资数量的 ,且不高于B种物资数量的 ,A、B两种物资的单价分别是150元/套、100元/套.设购买A种物资x套,购买这两种物资所需的总费用为y元.(1)、直接写出y关于x的函数关系式;(2)、求总费用y的最小值;(3)、若实际购买时,A种物资单价下调 元/套,B种物资单价上调了m元/套,此时购买这两种物资所需最少费用为23500元,直接写出m的值.23. 已知正方形 的对角线 、 交于O,M是 上一点.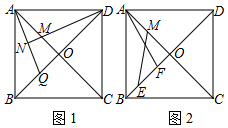 (1)、如图1, 于点N,交 于点Q;
(1)、如图1, 于点N,交 于点Q;①求证: ;
②若 ,求证: ;
(2)、如图2,M是 的中点,线段 (点E在点F的左边)在直线 上运动,连接 、 若 ,直接写出 的最小值.24. 直线 : 交x轴于A,交y轴于B.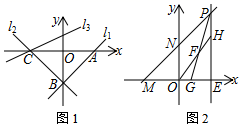 (1)、求 的长;(2)、如图1,直线 关于y轴对称的直线 交x轴于点C,直线 : 经过点C,点D、T分别在直线 、 上.若以A、B、D、T为顶点的四边形是平行四边形,求点D的坐标;(3)、如图2,平行y轴的直线 交x轴于点E,将直线 向上平移5个单位长度后交x轴于M,交y轴于N,交直线 于点P.点 在四边形 内部,直线 交 于G,直线 交 于H,求 的值.
(1)、求 的长;(2)、如图1,直线 关于y轴对称的直线 交x轴于点C,直线 : 经过点C,点D、T分别在直线 、 上.若以A、B、D、T为顶点的四边形是平行四边形,求点D的坐标;(3)、如图2,平行y轴的直线 交x轴于点E,将直线 向上平移5个单位长度后交x轴于M,交y轴于N,交直线 于点P.点 在四边形 内部,直线 交 于G,直线 交 于H,求 的值.